Unter der Reaktionsgeschwindigkeit versteht man die zeitliche Änderung der Konzentration eines Stoffes bei einer chemischen Reaktion[1].
Die physikalische Einheit der Konzentration ist mol/l, die zeitliche Änderung der Konzentration muss also in mol/l pro Sekunde oder Minute angegeben werden, geschrieben als mol * l-1 * s-1 bzw. min-1.
Messung der Reaktionsgeschwindigkeit
Für die Schulchemie sind zwei Methoden zur Messung der Reaktionsgeschwindigkeit wichtig, die volumetrische Messung mittels Kolbenprober sowie die gravimetrische Messung mittels Analysewaage.
Beide Methoden eignen sich aber nur für Reaktionen, bei denen ein Gas freigesetzt wird, zum Beispiel die Umsetzung von Salzsäure mit Magnesium oder die Reaktion von Essigsäure mit Calciumcarbonat. Gut ausgestattete Schulen verfügen auch über ein oder mehrere Photometer, mit denen sich die Geschwindigkeiten von Reaktionen sehr gut kontinuierlich messen und dokumentieren lassen.
Bei der volumetrischen Methode wird das gebildete Gas in einem Kolbenprober aufgefangen, aus der zeitlichen Volumenzunahme kann dann die Reaktionsgeschwindigkeit der Gasbildung berechnet werden.
Bei der gravimetrischen Methode für die Gasentwicklung zu einem Gewichtsverlust, aus dem dann ebenfalls die Reaktionsgeschwindigkeit berechnet werden kann. Nähere Ausführungen dazu siehe "Messung der Reaktionsgeschwindigkeit" auf den Seiten der Stufe EF.
Bei der photometrischen Methode führt man eine Reaktion durch, bei der sich die Farbe der Lösung ändert und misst den Farbumschlag quantitativ mit einem Photometer.
Hat die Schule kein Photometer zur Verfügung, kann man auch die einfach durchzuführende Versuch Umsetzung von Natriumthiocyanat mit Salzsäure als Schülerversuch durchführen. Bei dieser Reaktion reagieren die beiden klaren Lösungen zu einem trüben Produktgemisch. Der entstehende Schwefel macht das Produktgemisch immer undurchsichtiger. Man kann nun einfach die Zeit messen, die der Versuch benötigt, bis man durch den Erlenmeyerkolben nicht mehr hindurch sehen kann. Hier dient quasi das menschliche Auge als Photometer. Einzelheiten dazu siehe "Der Salzsäure-Thiosulfat-Versuch" auf den EF-Seiten.
Grundbegriffe
Durchschnittsgeschwindigkeit
Man misst die Konzentration c1 eines Eduktes oder Produktes zum Zeitpunkt t1, anschließend wiederholt man die Messung und misst die veränderte Konzentration c2 zum Zeitpunkt t2. Die Durchschnittsgeschwindigkeit ist dann
$\overset{\scriptscriptstyle-}{v} = \frac{c_{2} - c_{1}}{t_{2} - t_{1}}$
Falls der Browser die Formeln auf dieser Seite nicht richtig darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist der Browser veraltet, oder es besteht im Augenblick keine Internetverbindung.
Momentangeschwindigkeit
Während die Durchschnittsgeschwindigkeit sehr leicht zu berechnen ist, kann die Momentangeschwindigkeit oft nur sehr schwierig bestimmt werden. Unter der Momentangeschwindigkeit versteht man nämlich die Reaktionsgeschwindigkeit zu einem definierten Zeitpunkt t. Mathematisch gesehen ist die Momentangeschwindigkeit die Durchschnittsgeschwindigkeit über eine Zeitspanne, die gegen Null geht.
Stellt man beispielsweise die Zunahme des Wasserstoff-Volumens in einem Kolbenprober mit der Zeit graphisch als Kurve dar, dann wäre die Momentangeschwindigkeit zu einem beliebigen Zeitpunkt t die Tangente an der Kurve zu diesem Zeitpunkt. Die Durchschnittsgeschwindigkeit dagegen wäre eine Sekante, die die Kurve an zwei Stellen schneidet.
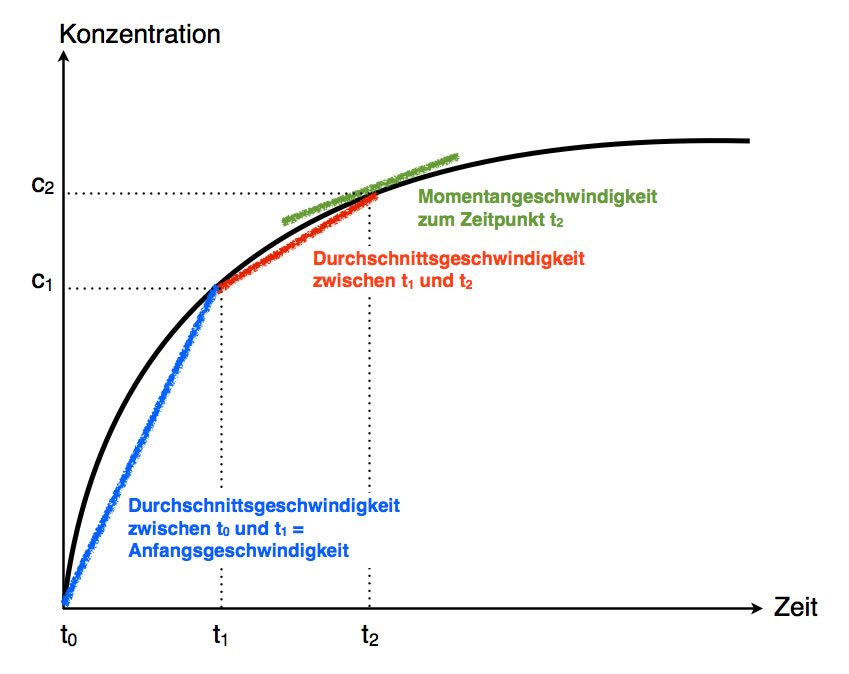
Anfangsgeschwindigkeit, Durchschnittsgeschwindigkeit und Momentangeschwindigkeit einer Reaktion, bei der ein Produkt gebildet wird
Autor: Ulrich Helmich 2021, Lizenz: Public domain.
Anfangsgeschwindigkeit
Darunter versteht man die Reaktionsgeschwindigkeit zu Beginn einer chemischen Reaktion. Als Momentangeschwindigkeit ist die Anfangsgeschwindigkeit sehr schwer zu messen, daher verwendet man hierfür meistens die Durchschnittsgeschwindigkeit während der ersten fünf oder zehn Sekunden der Reaktion - die Zeitspanne richtet sich natürlich nach der Art der Reaktion selbst.
Bei einer schnell ablaufenden Reaktion wie beispielsweise der Neutralisation einer Säure ist die Reaktion bereits nach Bruchteilen einer Sekunde vollständig beendet; mit Schulmitteln kann man hier so gut wie unmöglich eine Anfangsgeschwindigkeit bestimmen.
Bei der beliebten Umsetzung von Salzsäure mit Zink oder Magnesium misst man, welches Wasserstoff-Volumen sich in den ersten fünf bis zehn Sekunden der Reaktion bildet. Variiert man dabei die Konzentration der Säure, kann man sehr schön die Abhängigkeit der Reaktionsgeschwindigkeit von der Konzentration der Säure darstellen.
Vertiefungen
Nähere Ausführungen zum Thema Reaktionsgeschwindigkeit finden sich auf den Seiten zur Reaktionskinetik der Stufe EF:
- Die Geschwindigkeit chemischer Reaktionen
- Von welchen Faktoren hängt die Reaktionsgeschwindigkeit ab?
- Messung der Reaktionsgeschwindigkeit
- Konzentrationsabhängigkeit der Reaktionsgeschwindigkeit
- Durchschnittsgeschwindigkeit und Momentangeschwindigkeit
- Der Salzsäure-Thiosulfat-Versuch - ein bimolekulare Reaktion
- Reaktionsordnung (mono-, bimolekulare Reaktionen)
- Temperatur und Geschwindigkeit, RGT-Regel und Stoßtheorie
Historisches [2]
Erste Versuche
Der erste dokumentierte Versuch zur Reaktionsgeschwindigkeit wurde 1762 von Joseph Black durchgeführt. Er maß die Zeit, die es braucht, bis eine bestimmte Menge Eis bzw. Wasser sich um 8 ºC erwärmt. Für Wasser ermittelte er eine Reaktionszeit von ½ Stunde, für Eis maß er 10½ Stunden.
1777 führte Carl Friedrich Wenzel Versuche durch, wie sie heute fast noch in jeder Schule gemacht werden: Er löste Metalle in einer Säure mit unterschiedlichen Konzentrationen auf. Wenn sich Zink in der Säure in einer Stunde löste, dann brauchte der Auflösungsvorgang zwei Stunden, wenn die Säure nur halb so konzentriert war.
Ludwig Wilhelmy (1812-1864)
Dieser deutsche Chemiker aus Heidelberg führte um 1850 die ersten systematischen Untersuchungen zur Reaktionsgeschwindigkeit durch, die auch heutige Standards noch erfüllen würde. Er untersuchte die saure Hydrolyse von Saccharose in Fructose und Glucose. Kurz vorher hatte man entdeckt, dass Mono- und Disaccharide polarisiertes Licht spezifisch um einen bestimmten Winkel drehen können, was man mit einem Polarimeter gut messen kann. Bei der Hydrolyse von Saccharose ändert sich der Drehwinkel kontinuierlich, erst schnell, dann immer langsamer. Am Ende, wenn die Reaktion beendet ist, bleibt er konstant. Mit Hilfe dieser Technik konnte Wilhelmy die Stoffumsätze während des Ablaufs der Hydrolyse kontinuierlich verfolgen. Er stellte fest, dass die Reaktionsgeschwindigkeit sowohl von der Konzentration der Saccharose abhängt wie auch von der Art und der Konzentration der Säure. Er stellt dann das folgende Geschwindigkeitsgesetz auf:
$(1) -\frac{dZ}{dT} = M\cdot Z\cdot S$
Heute würde man diese Gleichung so formulieren:
$(2) \frac{dc}{dt} = K\cdot [Z]\cdot [S]$
Dabei ist $\frac{dc}{dt}$ die Reaktionsgeschwindigkeit, K die Geschwindigkeitskonstante, [Z] die Konzentration des Zuckers (Disaccharid) und [S] die Säurekonzentration. Wilhelmy vermutete also zunächst, dass die Hydrolyse eine Reaktion 2. Ordnung ist.
Diese Formel überprüfte Wilhelmy dann systematisch und stellte schließlich fest, dass die Reaktionsgeschwindigkeit $\frac{dc}{dt}$ nicht von der Säurekonzentration abhängt. Er fand heraus, dass es sich um eine monomolekulare Reaktion handelte.
Leider blieben Wilhelmys Forschungsergebnisse unbeachtet und wurden erst 1884 von Wilhelm Ostwald wiederentdeckt.
Marcellin Berthelot (1827 - 1907)
Dieser französische Forscher arbeitete um 1863 an einer Reaktion, die ebenfalls noch heute im Chemieunterricht eine große Rolle spielt, nämlich der Veresterung von Essigsäure mit Ethanol. Er verfolgte die Veresterung über mehrere Monate, bis sich die Konzentration der Essigsäure nicht mehr veränderte, weil das chemische Gleichgewicht erreicht war. Berthelot ging sehr systematisch vor und verwendete verschiedene Säuren und Alkohole und führte die Reaktion bei unterschiedlichen Temperaturen durch. Genial war seine Idee, auch die Rückreaktion zu verfolgen, bei der er Wasser und Ester reagieren ließ. Auch hier stellte sich nach langer Zeit die gleiche Gleichgewichtskonzentration ein wie bei der Hinreaktion.
Jacobus Henricus van’t Hoff
1877 wurde dann von van’t Hoff das Massenwirkungsgesetz aufgestellt, das er aus den Geschwindigkeitsgleichungen für die Veresterung herleitete, wie sie Berthelot formuliert hatte.
Quellen:
- Römpp Chemie-Lexikon, 9. Auflage 1992
- Weyer, Geschichte der Chemie, Band 2 - 19. und 20. Jahrhundert. Springer Spektrum 2018.