Zielsetzung
Wir wollen nun untersuchen, wie genau die Geschwindigkeit der H2-Bildung von der Konzentration der Salzsäure abhängt. Dass die Reaktionsgeschwindigkeit mit zunehmender Konzentration steigt, ist durch einfache Versuche bereits bestätigt worden. Zink oder Magnesium reagieren mit 2-molarer HCl deutlich heftiger und schneller als mit 0,5-molarer HCl.
Wir wollen nun aber einen quantitativen Zusammenhang zwischen c(HCl) und vR finden. Dazu gibt es mehrere mögliche experimentelle Vorgehensweisen, die sich auch mit Schulmitteln realisieren lassen. Für den normalen Schulunterricht haben sich die volumetrische Methode und die gravimetrische Methode gut bewährt (siehe letzte Seite). Mit einem Photometer ausgestattete Schulen können auch die photometrische Methode zur Bestimmung der Reaktionsgeschwindigkeit anwenden.
Auf dieser Seite konzentrieren wir uns aber auf die volumetrische Methode, also die Methode, die einen Kolbenprober verwendet, um das entstehende Wasserstoff-Volumen zu messen. Dabei gibt es eine recht aufwendige aber auch sehr genaue Methode, und eine genial einfache, aber sehr rechenintensive und auch nicht ganz so genaue Methode.
Variante 1: aufwendig aber genau
Der Kolbenprober-Versuch wird mit unterschiedlich konzentrierten HCl-Lösungen durchgeführt, zum Beispiel
- 2 mol/l
- 1 mol/l
- 0,5 mol/l
- 0,25 mol/l
- 0,125 mol/l
Ausgehend von einer 2-molaren Lösung, die ihnen zur Verfügung gestellt wird, können die Schülergruppen die Verdünnungsreihe selbst herstellen. Dabei haben sie Gelegenheit, sorgfältiges Arbeiten zu praktizieren.
Wir messen dann bei jedem Versuchsdurchgang das Wasserstoff-Volumen V(H2)10, das innerhalb der ersten zehn Sekunden der Reaktion entsteht. Bei der höchsten Konzentration von 2 mol/l muss man schon etwas aufpassen, dass einem der Kolben nicht nach hinten herausfliegt, so heftig ist die Reaktion, zumindest wenn man Magnesium-Pulver im Überschuss verwendet. Bei Magnesium-Spänen oder Zink-Pulver tritt dieses Problem nicht auf. Dafür hat man dann ein anderes Problem. Bei den stark verdünnten HCl-Lösungen entsteht mit Mg-Spänen oder Zn-Pulver so gut wie kein Wasserstoff mehr, jedenfalls nicht in den ersten 10 Sekunden. Daher verwende ich in meinem Unterricht immer Magnesium-Pulver.
Ein Kolbenprober ist mir dabei schon einmal kaputt gegangen, als der Kolben mit Macht nach hinten herausschoss, weil die Schüler ihn nicht festgehalten haben. Zum Glück ist er keinem Schüler vor den Kopf geflogen. Das hätte ziemlich weg getan.
Vor- und Nachteile: Diese Methode ist einerseits sehr materialaufwendig (vier bis fünf Kolbenprober werden pro Gruppe gleichzeitig gebraucht, und welche Chemiesammlung verfügt schon über 30 gute Kolbenprober?) oder sehr zeitaufwendig (wenn man nicht so viele Kolbenprober zur Verfügung hat, müssen fünf oder sechs Messungen nacheinander durchgeführt werden, selbst eine 90-Minuten-Stunde ist dann schon sehr knapp, wenn die S. nicht sehr gut vorbereitet sind).
Andererseits liefert diese Methode recht genaue Ergebnisse, vor allem muss man die S. nicht groß herumrechnen lassen, wenn sie die Reaktionsgeschwindigkeit in Abhängigkeit von der HCl-Konzentration darstellen sollen. Die S. verstehen diesen Versuch und die Sachzusammenhänge sofort.
Variante 2: einfach aber rechenintensiv
Wir benötigen nur einen einzigen Kolbenprober pro Gruppe, der absolut sauber arbeitet, bei dem der Kolben also nicht "hakelt", während er sich herausschiebt. Dann nehmen wir Salzsäure der Konzentration 1 mol/l und filmen den Kolbenprober mit unseren Smartphones, die dazu am besten in ein Stativ eingespannt werden, damit die Aufnahme nicht ruckelt. Der Versuch wird abgebrochen, wenn sich der Kolben nicht mehr merklich bewegt.
Vor- und Nachteile: Diese Methode ist einfach durchzuführen, aber die Auswertung der Ergebnisse den S. oft große Schwierigkeiten, da sie um mehrere Ecken denken müssen.
Ergebnisse nach Variante 1
Hier bekommt man sehr schnell heraus, dass die Reaktionsgeschwindigkeit linear mit der Konzentration der Salzsäure zunimmt - im Idealfall nach der Formel
$V(H_{2})_{10 s} = k \cdot c(HCl)$
Falls der Browser die Formeln auf dieser Seite nicht richtig darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist der Browser veraltet, oder es besteht im Augenblick keine Internetverbindung.
Mit dem Ausdruck auf der linken Seite der Formel ist das in den ersten 10 Sekunden gebildete Wasserstoff-Volumen gemeint, das quasi ein Maß für die Reaktionsgeschwindigkeit ist. Wenn man dieses Volumen kennt, kann man damit auch die Stoffmenge an Wasserstoff berechnen, die sich gebildet hat, und wenn man diese Stoffmenge durch die Zeit (10 Sekunden) teilt, erhält man die Durchschnittsgeschwindigkeit während der ersten 10 Sekunden. Diese Durchschnittsgeschwindigkeit ist der Konzentration c(HCl) proportional, und die Konstante k ist die sogenannte Geschwindigkeitskonstante.
Rechenbeispiel
Es wurden 50 ml HCl der Konzentration 1 mol/l verwendet. In den ersten 10 Sekunden wurden im Kolbenprober 26 ml Wasserstoff-Gas aufgefangen. Wie groß ist die durchschnittliche Reaktionsgeschwindigkeit während der ersten 10 Sekunden?
Oft rechnet man bei Wasserstoff-Gas unter Normalbedingungen mit einem Molvolumen von 24 Litern. Wenn wir also 26 ml aufgefangen haben, so entspricht das etwas mehr als 1 mmol H2; nämlich 26/24 = 1,083 mmol. Dieses Volumen hat sich während der ersten 10 Sekunden gebildet, also ist die durchschnittliche Reaktionsgeschwindigkeit während der ersten 10 Sekunden 0,1083 mmol * s-1 für V(HCl) = 0,05 Liter. Auf einen Liter bezogen, haben wir dann vR = 21,67 mmol * l-1 * s-1.
Ergebnisse nach Variante 2
Wenn man die Bewegung des Kolbens filmt und dann das Video auswertet, kann man eine Tabelle bzw. eine Graphik anfertigen, die vielleicht so aussieht:
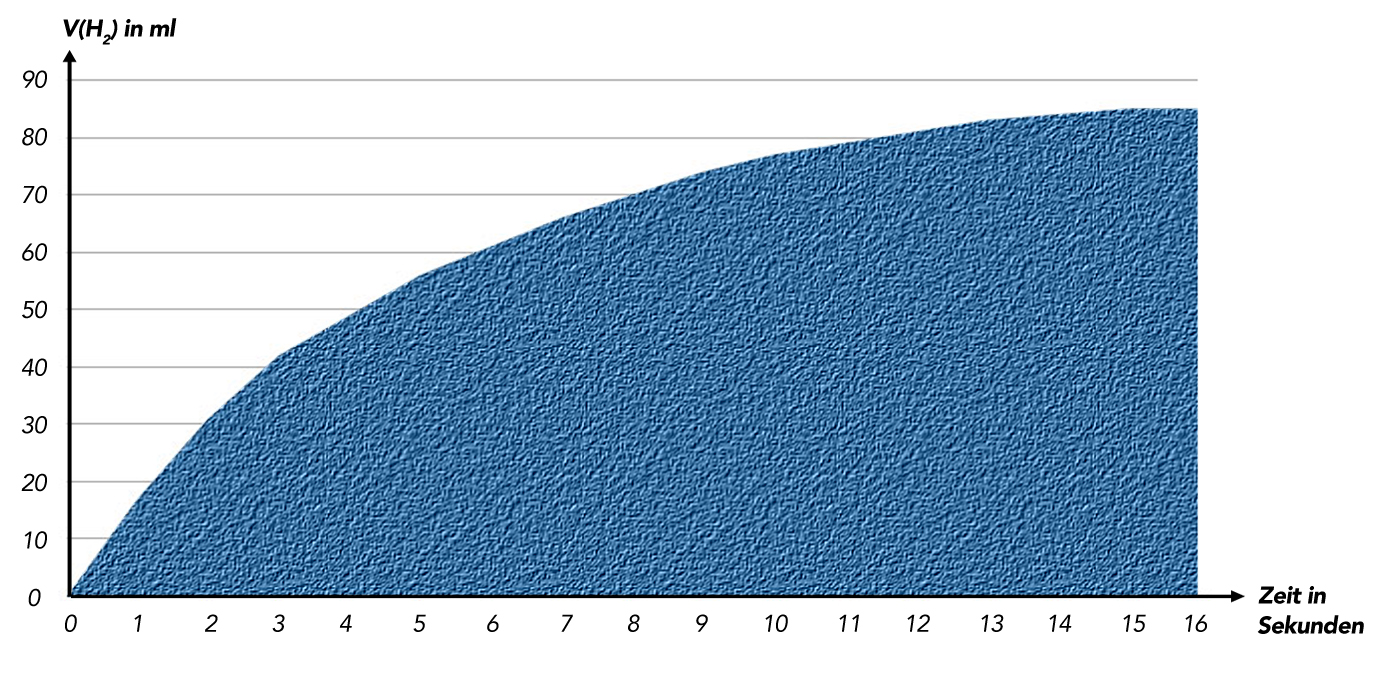
Graphische Darstellung der Zunahme von V(H2) gegen die Zeit
Autor: Ulrich Helmich, Lizenz: Public domain.
Im Laufe der Zeit wird pro Zeiteinheit immer weniger Wasserstoff gebildet, bis schließlich das Volumen im Kolbenprober gar nicht mehr zunimmt. Man sieht also sofort, dass die Reaktionsgeschwindigkeit als erste Ableitung der Volumenzunahme immer kleiner wird und gegen den Wert Null strebt.
Erster Rechenschritt:
Ermittlung der Durchschnittsgeschwindigkeiten
Wie entnimmt man jetzt der Graphik die Reaktionsgeschwindigkeit zum Zeitpunkt t? Idealerweise haben die Schülergruppen während des Versuchs die Ergebnisse tabellarisch protokolliert und aus diesen Daten dann die Graphik erstellt. Mit Hilfe einer Tabelle kann man nun recht leicht die durchschnittlichen Reaktionsgeschwindigkeiten in den verschiedenen Zeitintervallen ermitteln.
Rechenbeispiel
Wie hoch ist vR im Zeitintervall t6-t5?
Zum Zeitpunkt t5 konnte man am Kolbenprober ein Volumen von 61,5 ml H2-Gas ablesen, und zum Zeitpunkt t6 ein Volumen von 66,1 ml. In dieser einen Sekunde haben sich also 66,1 - 61,5 = 4,6 ml Wasserstoff gebildet.
Das entspricht einer Stoffmenge von 4,6 ml / 24 ml*mmol-1 = 0,19 mmol.
Angenommen, in dem Erlenmeyerkolben befanden sich 50 ml Salzsäure, dann hätte 1 Liter Salzsäure die 20fache Stoffmenge produziert, also 3,83 mmol. Somit wäre die Reaktionsgeschwindigkeit für das Zeitintervall t6-t5 ungefähr 3,83 mmol * l-1 * s-1.
Wenn wir die Messwerte in eine Tabellenkalkulation übertragen, wird die Berechnung der jeweiligen durchschnittlichen Reaktionsgeschwindigkeiten natürlich wesentlich einfacher, und die S. lernen nebenbei auch noch etwas Nützliches, das man auch in anderen Fächern gebrauchen kann, nicht nur in Chemie.
Zweiter Rechenschritt:
Ermittlung der jeweiligen HCl-Konzentrationen
Am Anfang hatten wir eine HCl-Konzentration von c(HCl) = 1,00 mol * l-1. Nach der ersten Sekunde konnten wir ein Wasserstoff-Volumen von ca. 18 ml ablesen.
Betrachten wir nun die Reaktionsgleichung, die dem Versuch zu Grunde liegt:
$Zn (s) + 2 \ HCl (aq) \to ZnCl_{2} (aq) + H_{2} (g)$
Wir sehen ganz klar: Wenn 1 mmol H2 entstanden ist, wurden dabei 2 mmol HCl verbraucht.
Rechenschritt 2.1: Berechnung von n(H2) und n(HCl)verbraucht
Berechnen wir zunächst die Stoffmenge n(H2), die während der ersten Sekunde entstanden ist:
$n (H_{2}) = \frac{18 \ ml}{24 \frac{ml}{mmol}} = 0,75 \ mmol$
Mit Hilfe der Reaktionsgleichung stellen wir dann fest, dass in der ersten Sekunde 1,5 mmol HCl verbraucht worden sind, also das Doppelte der Wasserstoff-Stoffmenge.
Rechenschritt 2.2: Berechnung von c(HCl)1s
Wie groß ist nach einer Sekunde nun die Konzentration c(HCl) im Erlenmeyerkolben?
Angenommen, es befanden sich 50 ml in dem Reaktionsgefäß, dann hatten wir bei 1-molarer Salzsäure eine Stoffmenge n(HCl) von genau 50 mmol. Um die Stoffmenge n(HCl)1s zu erhalten, die nach einer Sekunde im Kolben vorhanden ist, müssen wir die 1,5 mmol, die wir eben errechnet haben, von dieser Stoffmenge abziehen.
$n (HCl)_{1s} = 50 \ mmol - 1,5 \ mmol = 48,5 \ mmol$
Uns interessiert aber weniger die noch vorhandene Stoffmenge, sondern die Konzentration c(HCl) nach 1 Sekunde, also c(HCl)1s.
$c (HCl)_{1s} = \frac{n (HCl)_{1s}}{V(HCl)} = \frac{48,5 \ mmol}{0,05 \ l} = 0,097 \ mol/l$
Falls der Browser die Formeln auf dieser Seite nicht richtig darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist der Browser veraltet, oder es besteht im Augenblick keine Internetverbindung.
Es hilft jetzt kein Gejammere, wir müssen die HCl-Konzentrationen und die Durchschnittsgeschwindigkeiten für jeden einzelnen Zeitabschnitt berechnen. Das ist sehr aufwendig. Es sei denn, man hat nicht nur eine Tabellenkalkulation zur Verfügung, sondern kann damit auch umgehen.
Variante 2 mit Tabellenkalkulation
Angenommen, wir hätten die Messwerte eines solchen Versuchs sofort in eine Tabellenkalkulation eingetragen. Dann könnten wir die ganzen Berechnungen, die oben erklärt worden sind, "in einem Rutsch" durchführen lassen.
Hier sehen Sie die Ergebnisse eines Versuchs, den ich vor einigen Jahren mit meinen Schüler(innen) in der Stufe EF durchgeführt habe. Die Daten der Spalte 2 wurden von einem Schüler noch während des Versuchs in eine vorbereitete Tabellenkalkulation eingetragen. Die anderen Spalten wurden dann bei der Besprechung des Versuchs gemeinsam erarbeitet. Anschließend wurde noch die Graphik erzeugt, die in der Abbildung zu sehen ist. Die Graphik wurde dann von mir zu Hause mit Photoshop noch etwas bearbeitet.
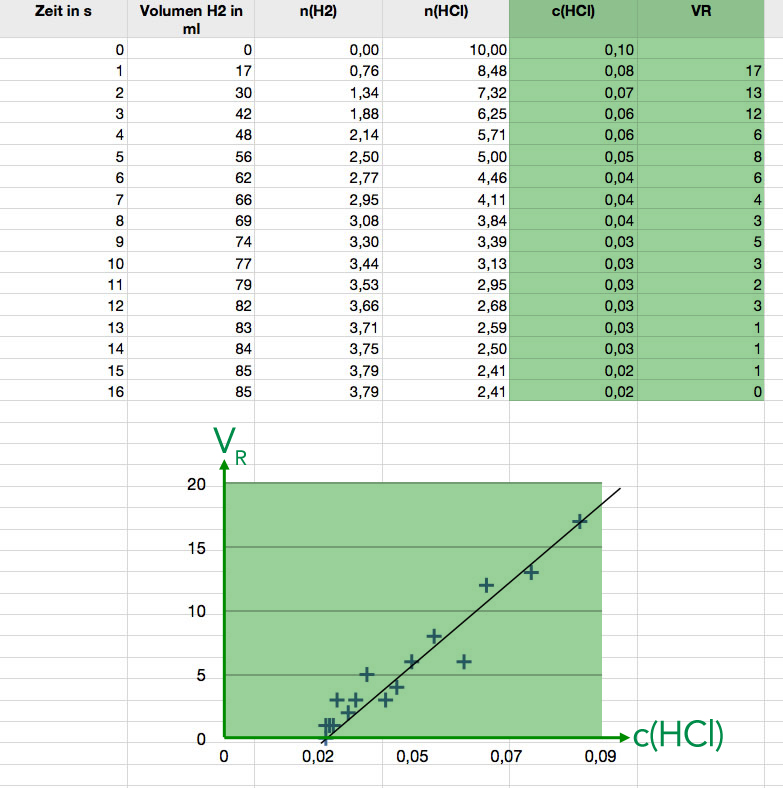
Bearbeiteter Screenshot der Tabellenkalkulation mit den gemessenen und anschließend berechneten Daten/Werten
Die beiden ersten Spalten enthalten die Messwerte, nämlich Zeit und V(H2). In der dritten Spalte wurde die Stoffmenge n(H2) aus dem Volumen V(H2) berechnet, in der vierten Spalte wurde dann die Stoffmenge n(HCl) berechnet, in der nächsten Spalte die Konzentration c(HCl). Die Reaktionsgeschwindigkeit wurde erst in der letzten Spalte berechnet (hier einfach als Differenz VN+1 - VN). Die beiden letzten Spalten wurden dann graphisch als xy-Diagramm dargestellt. Die Ausgleichsgerade wurde dann manuell in das Diagramm gelegt.
Man sieht hier eindeutig einen (mehr oder weniger) linearen Zusammenhang zwischen v(HCl) und der Reaktionsgeschwindigkeit:
VR = k * c(HCl) - x
An sich lautet die Geschwindigkeitsgleichung für eine Reaktion 1. Ordnung:
VR = k * c(A)
wenn A der Ausgangsstoff ist, von dessen Konzentration die Reaktionsgeschwindigkeit abhängt. Die obige Graphik sieht etwas anders aus, an sich müsste die Gerade ihren Ursprung bei (0,0) haben. Daher der Zusatzterm -x in der ersten Gleichung. Warum das bei dem Versuch so war, kann nur spekuliert werden; Schulversuche laufen meistens nicht allzu präzise ab.
Seitenanfang -
Weiter mit Durchschnitts- und Momentangeschwindigkeit ...