Bedeutung von B-Bäumen
B-Bäume sind von großer praktischer Bedeutung, weil sie speziell für große Datenmengen entwickelt wurden, die auf Festplatten, SSDs oder Datenbankservern gespeichert sind. Dort ist der Zugriff auf Datenblöcke viel teurer als im Arbeitsspeicher. B-Bäume reduzieren die Zahl dieser Zugriffe und sorgen dafür, dass Datenbanken, Dateisysteme und Suchstrukturen auch bei Millionen von Einträgen schnell bleiben.
Aufbau eines B-Baums
Wir betrachten hier einen "kleinen" statischen B-Baum mit einer Breite von 3. Das heißt, es passen genau drei Elemente in einen Knoten, flankiert von vier Zeigern auf Nachfolgerknoten. "Statisch" heißt hier, dass der B-Baum mithilfe von Arrays implementiert wird, die Größe der Knoten ist also nicht dynamisch veränderlich.

Der B-Baum nach Einfügen der ersten drei Zahlen
Der erste Knoten (die Wurzel des B-Baums) enthält drei Zahlen, die beim Einfügen in den Knoten aufsteigend sortiert worden sind. Die vier Nachfolger-Zeiger haben alle noch den Wert null.
Wenn der Knoten voll ist, kann keine neue Zahl mehr eingefügt werden. Bei einem B-Baum wird der volle Knoten vor dem Einfügen eines neuen Elementes gesplittet. Die mittlere Zahl, der sogenannte Median, wandert eine Ebene nach oben, wie auf dem nächsten Bild gezeigt.
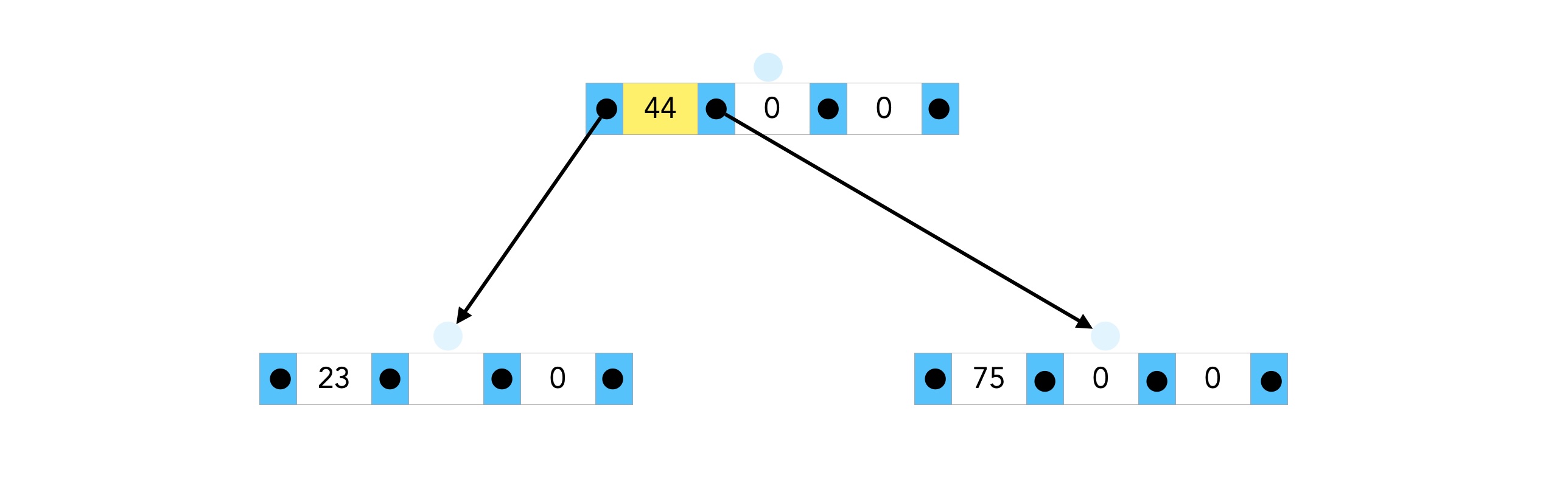
Der B-Baum vor dem Einfügen einer neuen Zahl und nach dem Splitten der alten Wurzel
Es entsteht ein neuer Wurzel-Knoten mit nur einem Element, dem Median 44 des alten Knotens. In der neuen Wurzel ist jetzt noch Platz für zwei weitere Elemente, und die beiden neuen Tochterknoten bieten ebenfalls Platz für je zwei weitere Elemente.
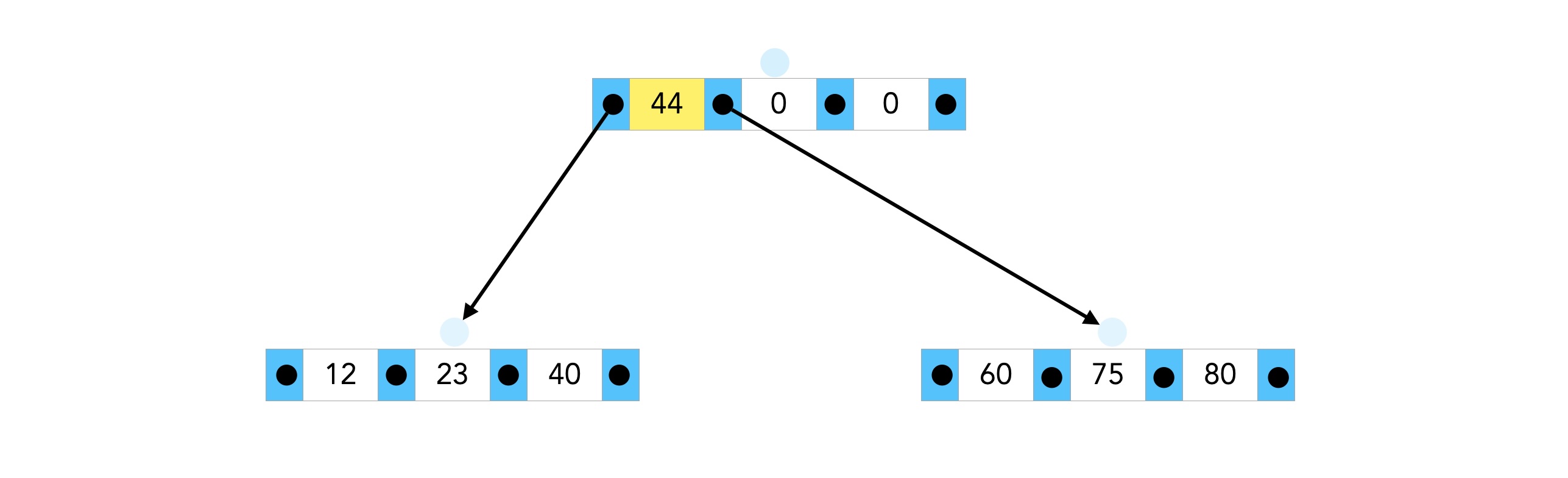
Der B-Baum nach Einfügen der Zahlen 60, 40, 12 und 80
Hier sehen wir den B-Baum nach dem Einfügen der Zahlen 60, 40, 12 und 80. Beide Nachfolgerknoten sind jetzt voll besetzt.
Wenn nun eine weitere Zahl in einen der beiden Nachfolger eingefügt werden soll, muss dieser wieder gesplittet werden, wobei der Median dieses Knotens dann eine Ebene weiter nach oben wandert. Das wollen wir einmal am Beispiel der Zahl 50 demonstrieren. Da 50 größer als 44 ist, muss sie in den rechten Nachfolger der 44 eingefügt werden. Diese Tatsache wird in dem nächsten Bild veranschaulicht:
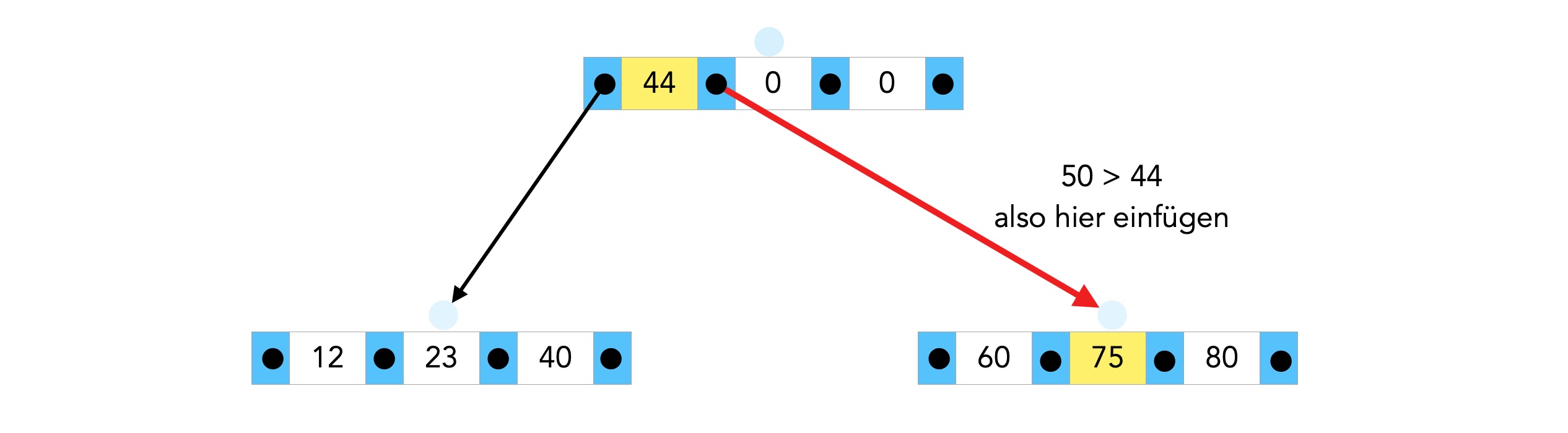
Der B-Baum vor dem Einfügen der 50
Vor dem Einfügen der 50 muss der rechte Nachfolger-Knoten noch gesplittet werden. Dazu muss der Median 75 dieses Knotens eine Ebene nach oben wandern. In der Wurzel ist noch Platz dafür. Gleichzeitig mit dem "Hochziehen" des Medians in den darüber liegenden Knoten wird der volle Knoten gesplittet; es entstehen zwei neue Knoten:
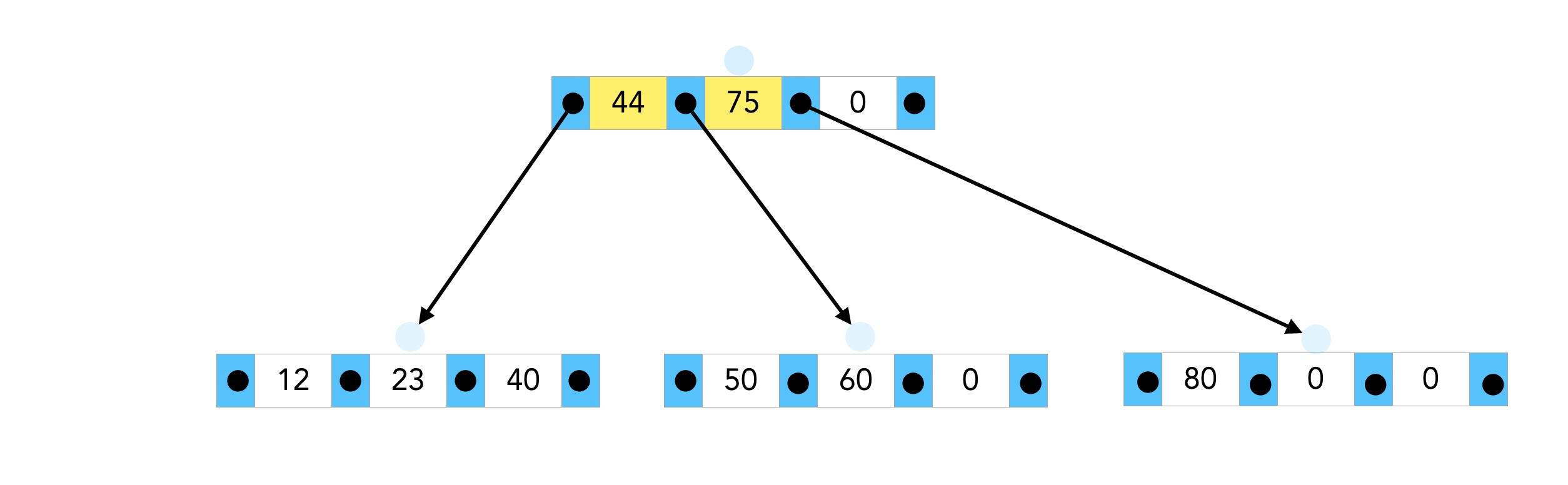
1.) Hochziehen des Medians
2.) Splitten des rechten Nachfolgers
Als Nächstes wollen wir die 30 einfügen. Da 30 kleiner als 44 ist, muss die 30 in den linken Nachfolger eingefügt werden:
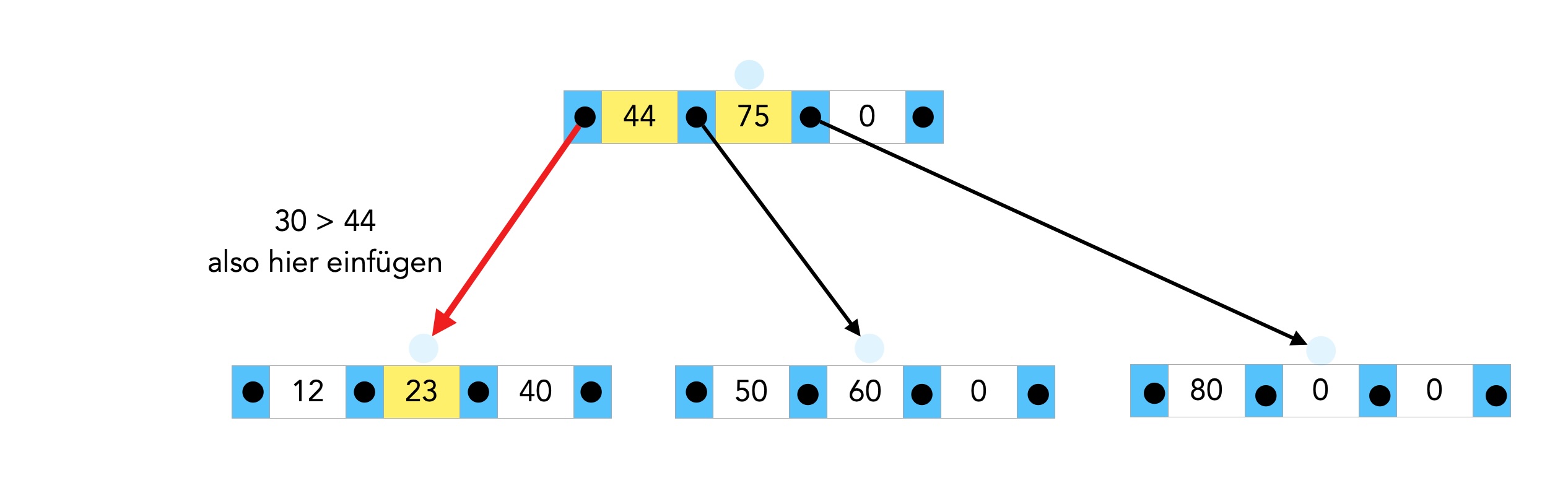
Vor dem Einfügen der 30 in den linken Nachfolger
Auch der linke Nachfolger muss jetzt in zwei neue Knoten gesplittet werden. Der Median - 23 - rückt dabei in die Wurzel auf, und der Knoten 12 - 23 - 40 wird gesplittet:
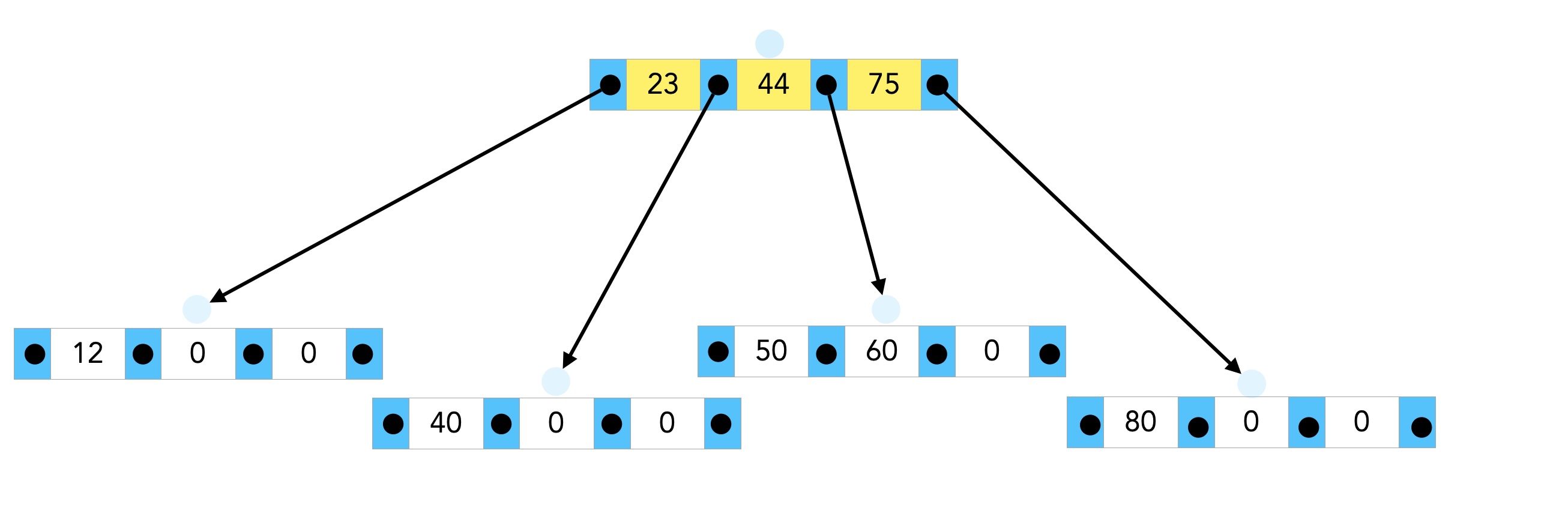
Nach dem Splitten des linken Knotens
Die Wurzel 23 - 44 - 75 hat jetzt keinen weiteren Platz mehr, aber die vier Nachfolger dieser Wurzel bieten noch Platz für weitere Zahlen. Die 30 kann jetzt also problemlos in den zweiten Nachfolger eingefügt werden:
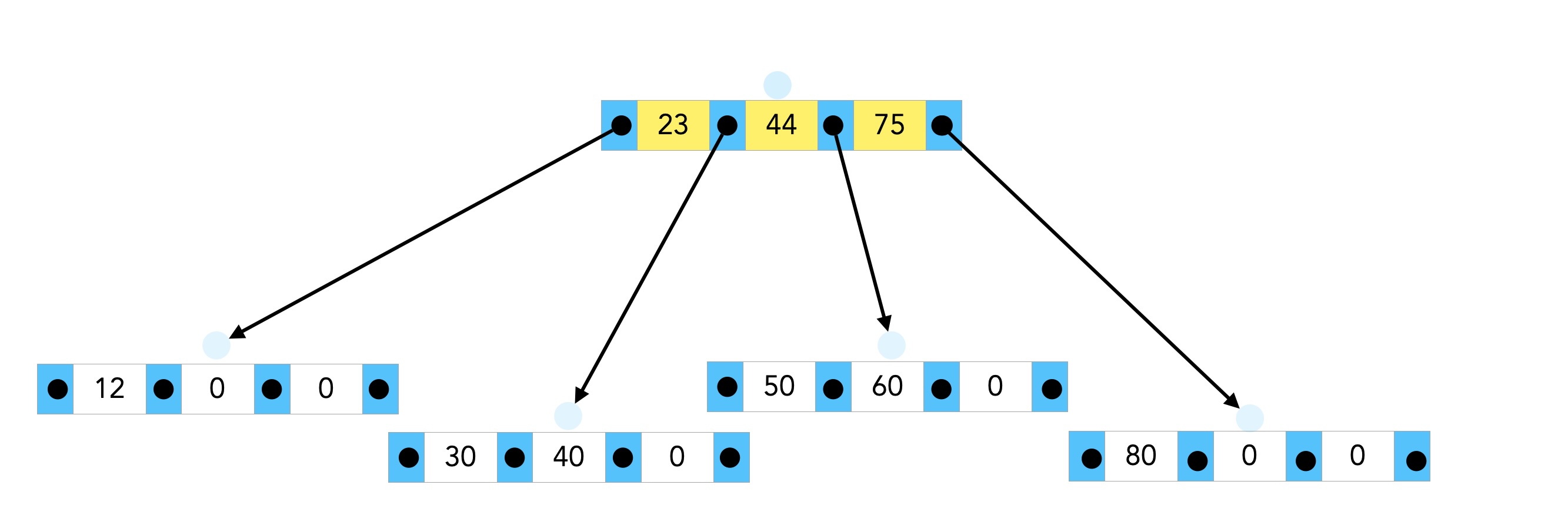
Nach dem Einfügen der 30 in den zweiten Nachfolger.
Wir fügen jetzt die 35 in den B-Baum ein. Dafür ist der zweite Nachfolger von links zuständig:
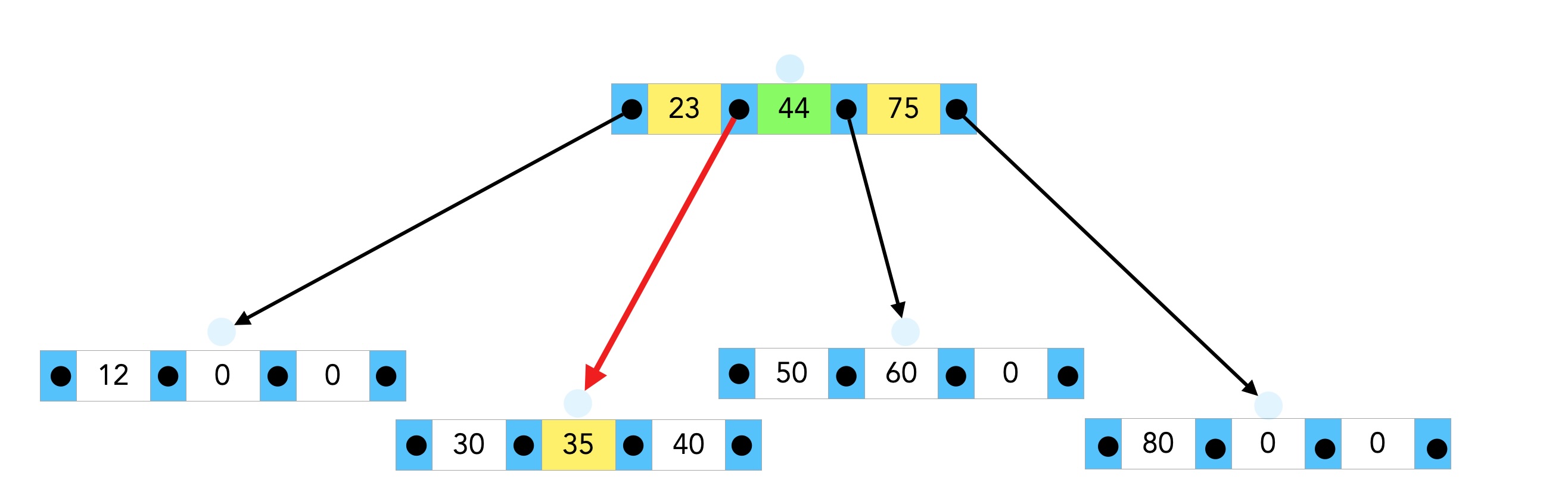
Nach dem Einfügen der 35 in den zweiten Nachfolger.
Nun wollen wir die 37 in den Baum einfügen. Der Zielknoten 30 - 35 - 40 ist allerdings voll besetzt und muss dafür gesplittet werden, wobei der Median 35 eine Ebene nach oben wandern müsste.
Der Wurzelknoten in der Ebene darüber ist aber ebenfalls voll besetzt. Bevor also der Median 35 nach oben wandert, muss die Wurzel gesplittet werden. Deren Median, die 44, müsste also ebenfalls eine Ebene nach oben wandern.
Im nächsten Bild sehen wir die Situation nach dem Splitten der alten Wurzel und dem Hochwandern des alten Medians:
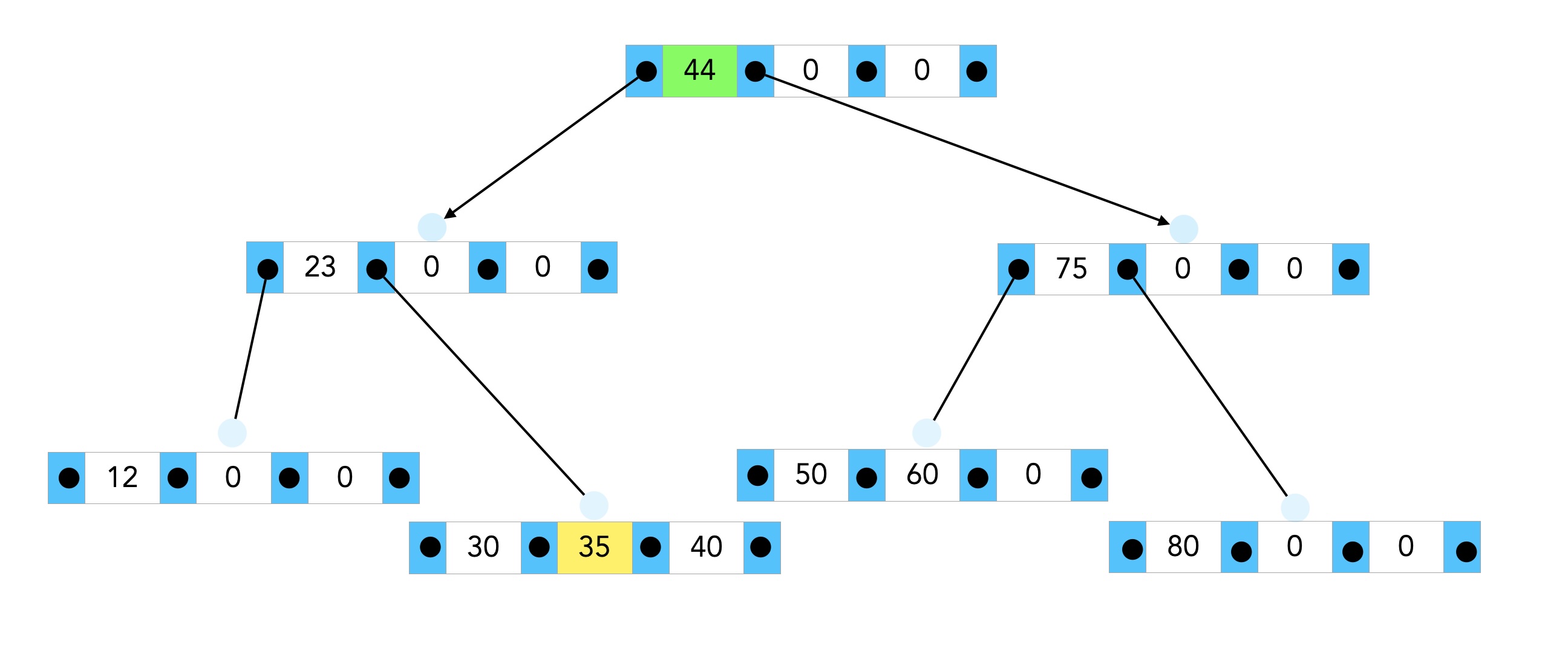
Nach dem Splitten der alten Wurzel
Der B-Baum besteht jetzt aus drei Ebenen, aber der Zielknoten 30 - 35 - 40 ist noch nicht gesplittet. Das holen wir jetzt nach:
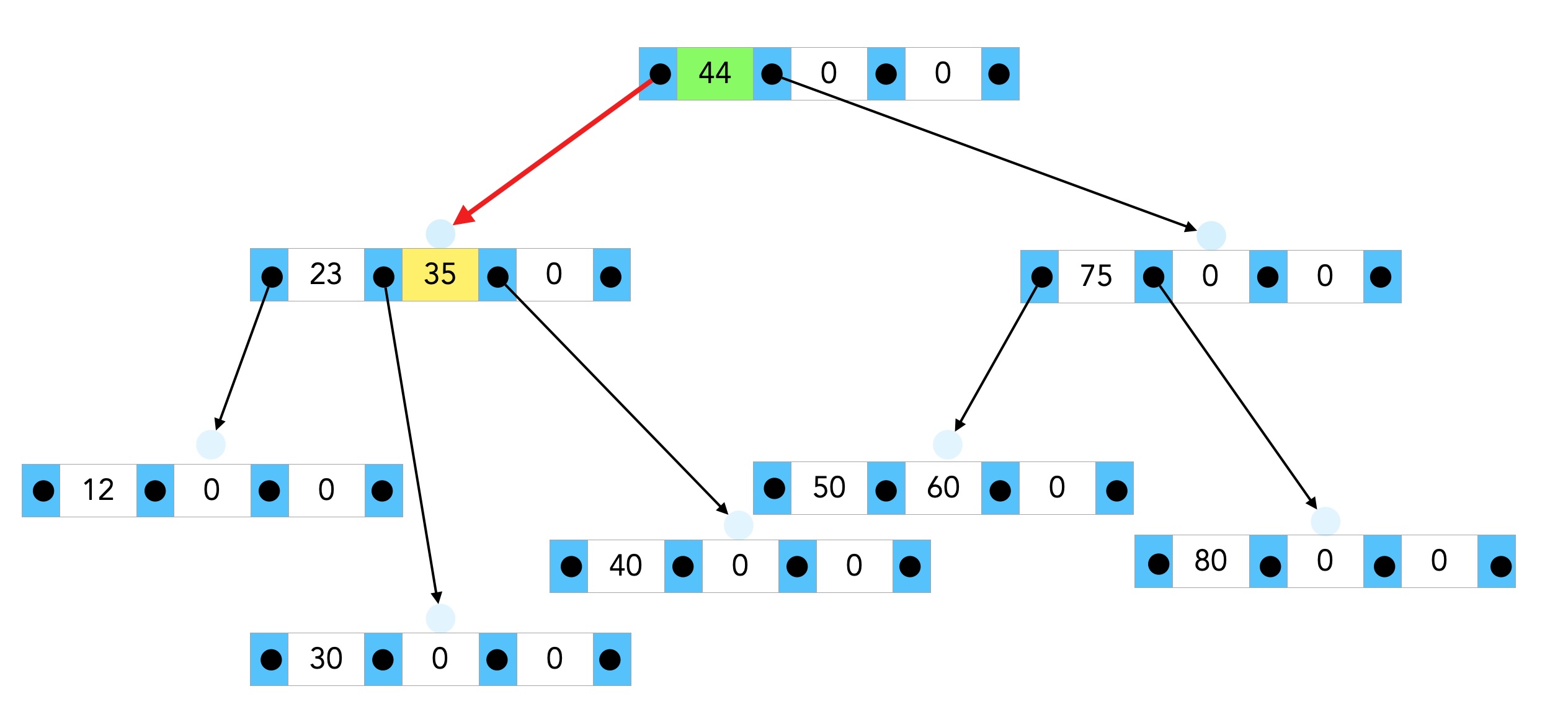
Nach dem Splitten des Nachfolgers 30-35-40
Nun kann die 37 in den neuen 40 - 0 - 0 - Nachfolger einsortiert werden.
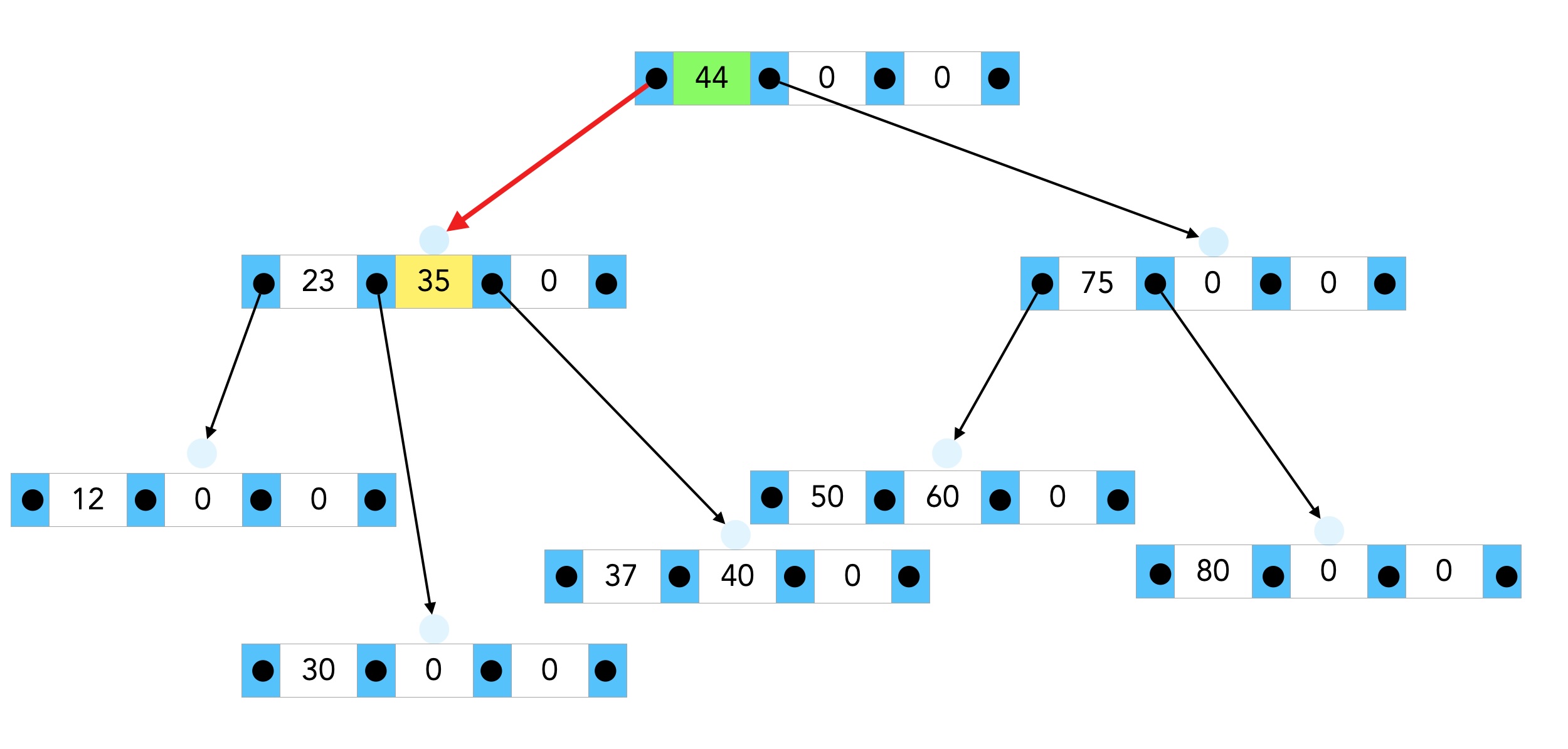
Nach dem Einfügen der 37
Damit wären wir erst mal am Ende dieser kleinen Präsentation. Die hier gezeigten Bilder stammen übrigens aus der neuen Präsentation von 2025, die Sie hier kostenlos herunterladen können.