Problemstellung
Jetzt kommen wir zu einem Thema, das eventuell im Abitur eine Rolle spielen könnte. In den 10 Jahren, seit in NRW das Zentralabitur durchgeführt wird, ist aber noch keine Aufgabe zum Thema "ausgeglichene Bäume" gestellt worden. Aber was nicht ist, kann ja noch kommen. Abgesehen davon ist das Thema wirklich sehr interessant und sollte eigentlich von jedem durchgearbeitet werden, der sich ernsthaft für Binärbäume interessiert.
Betrachten Sie doch bitte einmal folgenden binären Suchbaum:
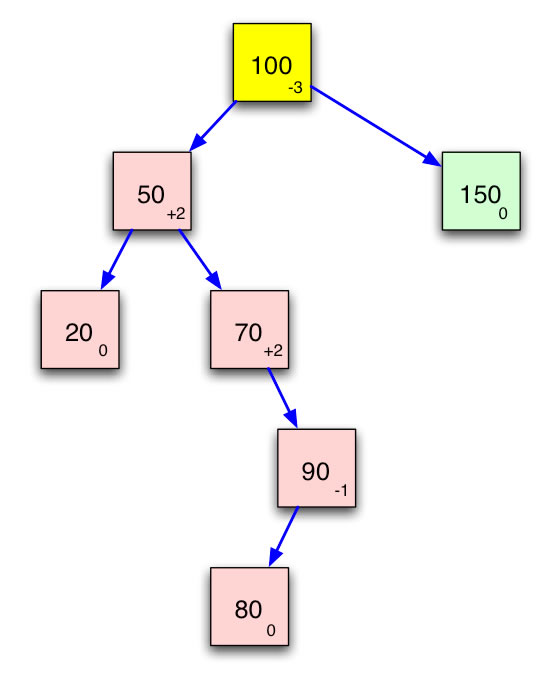
Ein mit Sicherheit nicht ausgeglichener binärer Suchbaum
Die kleinen Zahlen rechts unten in den Kästchen geben an, wie stark der jeweilige Knoten links- oder rechtslastig ist. Hat der linke Unterbaum des Knotens genau so viele Ebenen wie der rechte Unterbaum, so ist der Knoten bzw. der Unterbaum, der den Knoten zur Wurzel hat, ausgeglichen. Die Zahl -1 bedeutet, dass der linke Unterbaum des Knotens eine Ebene mehr hat als der rechte Unterbaum. Entsprechend bedeutet eine Angabe von +1, dass der rechte Unterbaum des Knotens eine Ebene mehr hat als der linke Unterbaum. Achten Sie auf die Wurzel 100 des Baums, hier hat die Bilanz sogar den Wert -3: Der linke Unterbaum hat vier Ebenen, der rechte aber nur eine.
Stellen wir den gleichen binären Suchbaum jetzt in ausgeglichener Form dar:
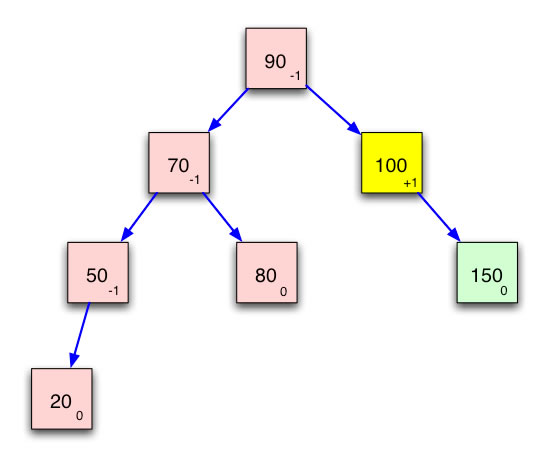
Der gleiche Baum, diesmal aber ausgeglichen
Bei einem vollständig ausgeglichenen Baum hat jeder Knoten die Bilanz 0. Allerdings ist dies in der Praxis kaum zu realisieren. Daher definiert man den Begriff "Ausgeglichener binärer Suchbaum" folgendermaßen:
Ausgeglichener binärer Suchbaum (AVL-Baum):
Ein binärer Suchbaum, bei dem jeder Knoten des Baums eine Bilanz von -1, 0 oder +1 hat.
Damit ist der Baum, der in Abb. 2 gezeigt wird, ein ausgeglichener binärer Suchbaum, der nach seinen "Entdeckern" Georgi Maximowitsch ADELSON-VELSKI und Jewgeni Michailowitsch LANDIS auch als AVL-Baum bezeichnet wird.
Frage:
Angenommen, wir würden die Zahl 170 in den Baum einfügen. Wie würde sich das auf die "Ausgeglichenheit" des Baumes auswirken?
Antwort:
Die Wurzel des Baumes 90 hätte die Bilanz 0. Das wäre auf den ersten Blick sogar ein Fortschritt. Schaut man sich dann aber den Knoten 100 an, so steigt dessen Bilanz auf +2, und damit wäre der Teilbaum mit der 100 als Wurzel rechtslastig und nicht mehr ausgeglichen. Ein Baum, der einen nicht ausgeglichenen Teilbaum enthält, ist aber insgesamt nicht ausgeglichen.