Eine mögliche Datenstruktur in Java
Wie könnte eine mögliche Datenstruktur für B-Bäume in Java aussehen? Wir wollen diese Datenstruktur von vornherein flexibel gestalten, es sollen also Knoten beliebiger Breite möglich sein.
public class Knoten
{
private Knoten[] next;
private int[] value;
private int count;
public int order;
...
Hier ein Vorschlag für eine solche Datenstruktur. Die Zahlen werden als int-Array value, die Nachfolger-Zeiger als Zeiger-Array next vom Typ Knoten angelegt. Das Attribut order speichert die Zahl der Elemente pro Knoten. In unserem eben behandelten Beispiel hätte order also den Wert 4, da vier int-Zahlen in einem Knoten gespeichert wurden. Wichtig ist auch das Attribut count, in diesem Attribut merkt sich ein Knoten-Objekt, wie viele Elemente bereits in dem Knoten enthalten sind. Bei einem neu erzeugten Knoten-Objekt hat count natürlich zunächst den Wert 0. Ist das Objekt voll belegt, hat count den Wert order-1, in unserem Beispiel also 3.
Ein Konstruktor für die Klasse Knoten
public Knoten(int n, int x)
{
order = n;
next = new Knoten[order+1];
value = new int[order];
for (int i=0; i < order; i++)
{
next[i] = null;
value[i] = 0;
}
next[order] = null;
value[0] = x;
count = 1;
}
Der Konstruktor erhält zwei Parameter, nämlich die Breite n des Knotens (beispielsweise 4), und die erste Zahl x, die in den Knoten eingefügt werden soll.
Das Attribut order speichert dann die Knotenbreite, dann wird der Array next mit order+1 Nachfolgerknoten angelegt, die zunächst mal leer sind (in der for-Schleife werden diese Zeiger auf null gesetzt). Schließlich wird der Array value für die eigentlichen Elemente erzeugt und mit Nullen initialisiert.
Nach der for-Schleife wird der ganz rechte Nachfolger-Zeiger des Knotens erzeugt und initialisiert, und schließlich wird die Zahl x in das erste Array-Element value[0] geschrieben und der Zähler count um 1 höher gesetzt.
Eine Einfüge-Methode
public void insertValue(int x)
{
if (count < order)
{
value[count] = x;
count++;
sort();
}
else
{
int i=0;
while ((i < count) && (x > value[i])) i++;
if (next[i] == null)
next[i] = new Knoten(order,x);
else
next[i].insertValue(x);
}
}
Zunächst wird geschaut, ob noch ein weiteres Element in den Knoten hineinpasst. Ist das der Fall (count < order), wird der Wert x in den ersten noch freien Speicherplatz geschrieben (value[count] = x) und count anschließend inkrementiert. Danach wird der Knoten neu sortiert. Dies geschieht durch den Aufruf der sort-Methode, auf die wir gleich noch kommen.
Alternativ hätte man den Knoten in der Reihenfolge mit Zahlen füllen können, wie sie eingefügt wurden, also unsortiert. Nach dem Einfügen der letzten Zahl hätte man dann sort aufrufen können. Wahrscheinlich wäre dieses Verfahren zeiteffizienter, da man nur einmal den Sortier-Algorithmus ausführen muss und nicht dreimal.
Ist der Knoten bereits voll besetzt, so muss der passende Nachfolgerknoten gefunden werden. Dazu wird der Wert der Zahl x nach und nach mit den Werten der im Knoten vorhandenen Zahlen verglichen. Solange x größer ist als die vorhandenen Werte, wird weiter gesucht (siehe while-Schleife). Ist der richtige next-Zeiger gefunden, so muss nachgeschaut werden, ob der Nachfolgeknoten bereits existiert oder ob ein neuer Nachfolgerknoten erst angelegt werden muss.
Das geschieht mit der if-Abfrage if (next[i] == null). Ist kein Nachfolger vorhanden, so wird mit der Anweisung next[i] = new Knoten(order,x) ein neuer Nachfolger angelegt. Andernfalls wird mit der Anweisung next[i].insertValue(x) die Zahl in den vorhandenen Nachfolger-Knoten geschrieben.
Die sort-Methode für einen Knoten
private void sort()
{
for (int i=0; i< count; i++)
for (int j=0; j < count-1; j++)
if (value[j] > value[j+1])
{
int temp = value[j];
value[j] = value[j+1];
value[j+1] = temp;
}
}
Wie man sofort sieht, handelt es sich hier um einen ganz einfachen Bubblesort. Da die Zahl der Knotenelemente nicht allzu groß ist, reicht hier der einfach zu implementierende Bubblesort völlig aus. Ein Quicksort für 5, 10 oder auch 20 Elemente wäre "mit Kanonen auf Spatzen schießen".
Die show-Methode für einen Knoten
public void show(int level)
{
for (int i=0; i<=count; i++)
{
if (next[i] != null)
next[i].show(level+1);
if (i < count)
System.out.println(level+" / "+value[i]);
}
}
Hier handelt es sich um eine typische inorder-Methode. Zunächst wird "nach links herabgestiegen". Wenn da nichts mehr zu erreichen ist, wird wieder aufgestiegen und nebenbei werden die unterwegs "gefundenen" Elemente ausgegeben. Der Ausgabe-Befehl schreibt nicht nur den Wert des jeweiligen Elements in die Konsole, sondern auch den Level, also die Ebene, auf der sich der Knoten befindet.
Ein Testprogramm für die Klasse Knoten
public class Test
{
Knoten kn;
public Test()
{
kn = new Knoten(5,12);
kn.insertValue(113);
kn.insertValue(45);
kn.insertValue(3);
kn.insertValue(6);
kn.insertValue(11);
kn.insertValue(100);
kn.insertValue(89);
kn.insertValue(47);
kn.insertValue(16);
kn.insertValue(24);
kn.insertValue(33);
kn.insertValue(19);
kn.insertValue(20);
kn.insertValue(21);
kn.insertValue(13);
kn.insertValue(27);
kn.insertValue(26);
kn.insertValue(35);
kn.insertValue(40);
kn.insertValue(42);
kn.insertValue(38);
kn.insertValue(41);
kn.insertValue(120);
kn.insertValue(122);
kn.insertValue(39);
kn.show(1);
}
}
Mit dieser Klasse wurde die Klasse Knoten getestet. Der Quelltext funktionierte problemlos. Die folgende Graphik zeigt den entstandenen B-Baum der Ordnung 5:
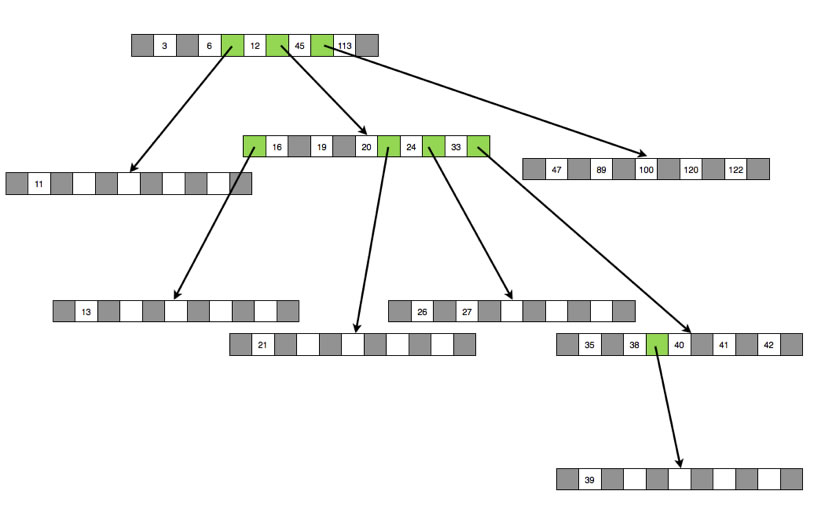
Der B-Baum aus der Klasse Test nach Einfügen aller Zahlen
Die next-Zeiger, die nicht auf null zeigen, sind grün markiert. Wie man leicht sieht, wurde hier sehr viel Speicherplatz verschenkt, die meisten Knoten enthalten leere Stellen. Bei einem richtigen B-Baum ist das anders, aber dazu kommen wir noch später.
Schauen wir uns nun die Ausgabe des Testprogramms an:
1 / 3 1 / 6 2 / 11 1 / 12 3 / 13 2 / 16 2 / 19 2 / 20 3 / 21 2 / 24 3 / 26 3 / 27 2 / 33 3 / 35 3 / 38 4 / 39 3 / 40 3 / 41 3 / 42 1 / 45 2 / 47 2 / 89 2 / 100 1 / 113 2 / 120 2 / 122
Die Ausgabe funktioniert genau so, wie sie theoretisch funktionieren sollte. Zunächst werden die beiden ersten Zahlen des Wurzel-Knotens ausgegeben, da hier noch keine Zeiger existieren, die auf andere Knoten zeigen. Nun kommt der Zeiger zwischen der 6 und der 12, der auf einen Knoten der Ebene 2 verweist. Also wird zunächst dieser Knoten ausgegeben. Hier steht nur die Zahl 11, daher wird "2 / 11" angezeigt. Nun geht es zurück zum Wurzelknoten, und die 12 wird ausgegeben. Wieder kommt ein Zeiger auf einen untergeordneten Knoten. Nun wird aber nicht die 16, das erste Element dieses Knotens ausgegeben, sondern der erste Zeiger des Knotens zeigt auf einen weiteren Knoten in der Ebene 3. Also muss zunächst dieser abgearbeitet werden. Das einzige Element dieses Knotens wird dann mit "3 / 13" ausgegeben. Und so geht das weiter, bis schließlich alle Elemente in geordneter Reihenfolge ausgegeben worden sind.
B-Bäume wurden übrigens 1972 von Rudolf BAYER entwickelt. Sie werden in den Indexdateien von großen Datenbanken eingesetzt, üblich sind Ordnungen von 1024 oder mehr, d.h., dass in einem einzigen Knoten 1024 Elemente gespeichert werden können. Und diese Elemente sind keine einfachen int-Zahlen wie in unserem Beispiel, sondern komplexe Datensätze bzw. Zeiger auf komplexe Datensätze.