Grundidee
Wie kann man die Vorteile von Arrays und die von Suchbäumen miteinander in Verbindung bringen? Neben den AVL-Bäumen spielen vor allem die Bayer-Bäume oder kurz B-Bäume eine wichtige Rolle bei alltäglichen Anwendungen wie zum Beispiel großen Datenbanken. Wir wollen auch hier keine Java-Quelltexte entwickeln, sondern uns einfach mal etwas oberflächlich mit dem Thema beschäftigen, zumal das Thema B-Bäume überhaupt nicht im Kernlehrplan Informatik der meisten Bundesländer auftaucht.
Bauen wir doch einen solchen B-Baum der Ordnung 4 einfach mal auf. Das heißt, ein Knoten des B-Baums soll vier Zahlen speichern können. "Richtige" B-Bäume, wie sie in Datenbanken eingesetzt werden, haben eine Ordnung von 512, 2014 oder größer, können also pro Knoten 1024 Datensätze oder mehr speichern. Der Übersichtlichkeit wegen beschränken wir uns hier auf 4 Datensätze pro Knoten, und die "Datensätze" sind einfache int-Zahlen. Bei einer richtigen Datenbank würde statt einer int-Zahl ein Zeiger auf die eigentlichen Daten gespeichert.
Fügen wir nun in einen leeren Knoten die Zahl 360 ein:
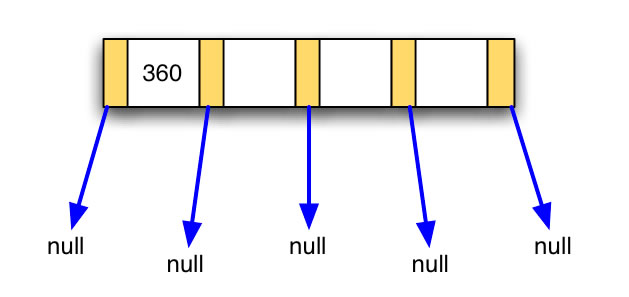
Nach Einfügen der Zahl 360
Die weißen Kästchen in der Abb. 1 enthalten die eigentlichen Daten, in unserem Fall also int-Zahlen. Die gelben Kästchen speichern die Adresse der Nachfolgerknoten - schließlich handelt es sich ja um einen Baum, und ein Baum besteht immer aus Knoten mit Nachfolgern.
Fügen wir nun die nächste Zahl ein, die 200:
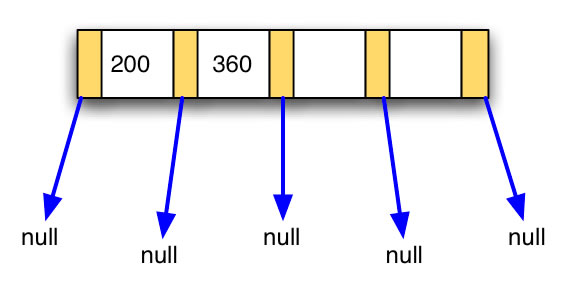
Nach Einfügen der Zahl 200
Die 200 wird jetzt vor die 360 gesetzt, weil die neue Zahl kleiner ist als die alte Zahl. Sonst tut sich nichts weiter; der B-Baum besteht immer noch aus nur einem Knoten.
Der Knoten eines B-Baums der Ordnung 4 fasst genau vier Daten, hier also vier int-Zahlen. Eine neue int-Zahl wird entweder sofort an die richtige Stelle in den Knoten eingefügt, oder alternativ wird der Knoten erst dann sortiert, wenn er vier int-Zahlen enthält. Von der Laufzeit her sollte das eigentlich keinen großen Unterschied machen.
Wir fügen jetzt zwei weitere int-Zahlen als Daten in den Knoten des B-Baums ein:
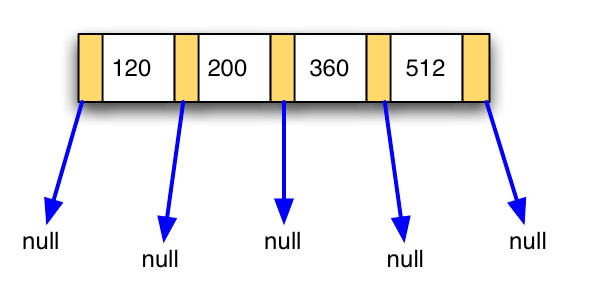
Nach Einfügen von 120 und 512
Jetzt wird es langsam interessant. Der Knoten ist voll, er kann keine weiteren Zahlen mehr aufnehmen. Wir wollen jetzt die Zahl 170 eingefügen:
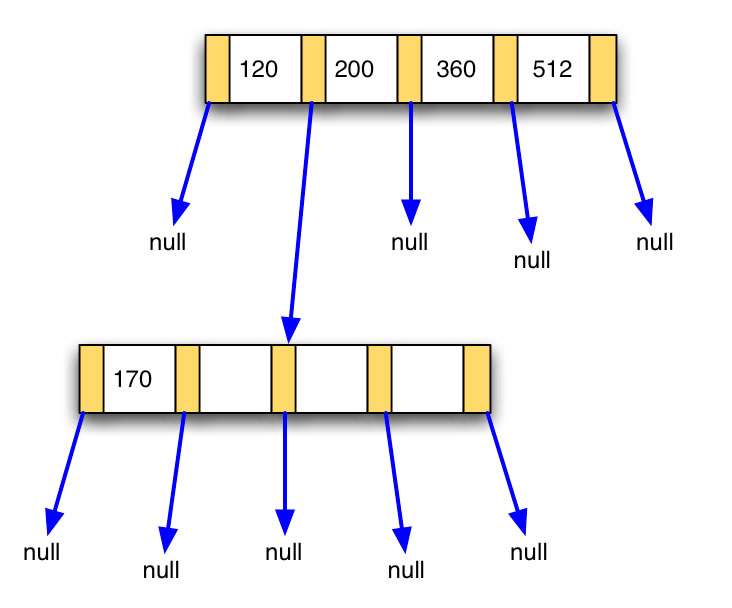
Nach Einfügen der Zahl 170
Die 170 passt nicht mehr in den ersten Knoten, daher wird nach einer passenden Einfügeposition gesucht und zwischen 120 und 200 gefunden. Dafür muss jetzt ein neuer Knoten angelegt werden, die wieder vier int-Zahlen fasst. In diesen neuen Knoten schreiben wir die 170. Und dann lassen wir den passenden Nachfolger-Zeiger des bisherigen Knotens auf den neuen Knoten zeigen.
Jetzt wollen wir die Zahlen 150, 510, 480, 500 und 511 einfügen:
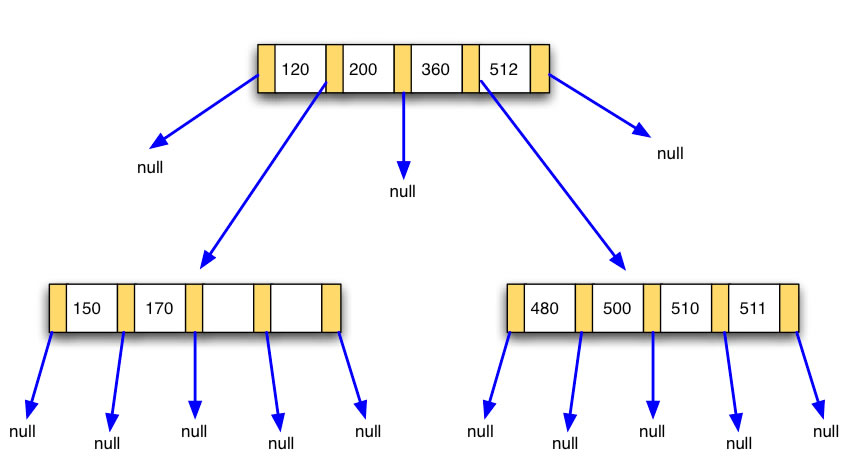
Nach Einfügen weiterer Zahlen
Nach Einfügen dieser fünf Zahlen ist ein zweiter Tochterknoten dazugekommen. Die 170 wurde in den linken Tochterknoten hinter die 150 gesetzt, weil sie größer ist als 150. Die vier anderen Zahlen liegen alle im Bereich zwischen 360 und 512, also werden sie in den gleichen Knoten eingefügt und aufsteigend sortiert.
Würden wir jetzt die Zahl 505 in den B-Baum einfügen, müsste ein neuer Knoten angelegt werden. Ein Nachfolger-Zeiger des rechten Tochterknotens würde dann auf diesen neuen Knoten zeigen, und zwar der Nachfolger-Zeiger zwischen der 500 und der 510.