Das Massenwirkungsgesetz und die Estersynthese
Auf der letzten Seite haben wir 1 mol Essigsäure mit 1 mol Ethanol bei Zimmertemperatur reagieren lassen. Als Katalysator hatten wir Schwefelsäure zugesetzt, so dass sich das chemische Gleichgewicht innerhalb weniger Stunden einstellt. Ohne Katalysator würde es über ein Jahr dauern, bis sich bei Zimmertemperatur das Gleichgewicht einstellt. Als Gleichgewichtskonstante hatten wir den Wert 4,12 errechnet.
Was geschieht aber, wenn wir am Anfang nicht 1 mol Essigsäure und 1 mol Ethanol reagieren lassen, sondern 2 mol Essigsäure und 1 mol Ethanol. Die Gleichgewichtskonstante verändert sich dabei nicht, sonst wäre es ja keine Konstante.
Es stellt sich folgendes Gleichgewicht ein:
$K=\frac{0,848\frac{mol}{l}*0,848 \frac{mol}{l}}{1,152 \frac{mol}{l}*0,152 \frac{mol}{l}} = 4,12$
Im Gleichgewicht haben wir noch 1,152 mol Essigsäure, das heißt 2 - 1,152 = 0,848 mol Essigsäure haben mit 0,848 mol Ethanol zu 0,848 mol Ester und 0,848 mol Wasser reagiert. Von dem Alkohol sind im Gleichgewicht noch 1 - 0,848 = 0,152 mol übrig.
Auf diese Konzentrationen kommt man entweder durch Auflösen einer komplizierteren quadratischen Gleichung, darauf möchte ich jetzt nicht näher eingehen, oder durch "Herumprobieren" mit einer Tabellenkalkulation - so habe ich es gemacht.
Kleiner mathematischer Exkurs
Wir sind jetzt zwar nicht im Mathematik-Unterricht, sondern wollen uns mit den chemischen Konsequenzen beschäftigen. Aber interessant ist, dass es zwei Randbedingungen gibt, die bei der Berechnung der Gleichgewichtskonzentrationen eine wichtige Rolle spielen.
1. Randbedingung
c(Ester) = c(Wasser)
Für jedes Molekül Ester, das entsteht, bildet sich auch genau ein Molekül Wasser.
2. Randbedingung
c(Säure) = c0(Säure) - c(Ester)
c(Alkohol) = c0(Alkohol) - c(Ester)
Die Gleichgewichtskonzentrationen von Säure und Alkohol berechnen sich aus den Anfangskonzentrationen c0() sowie aus der Gleichgewichtskonzentration des Esters.
Für Experten
Für die mathematisch Interessierten habe ich eine vierseitige PDF-Datei geschrieben, in der ich genau Schritt für Schritt erläutere, wie man aus dem Massenwirkungsgesetz eine quadratische Gleichung erstellt und diese dann auch löst.
Chemische Konsequenzen
Unter chemischen Aspekten ist Folgendes interessant: Durch die Erhöhung der Konzentration der Essigsäure ist die Ausbeute an Ester gestiegen, wenn man den eingesetzten Alkohol betrachtet. Haben vorher nur 67% des Alkohols reagiert, so werden bei doppelter Essigsäurekonzentration fast 85% des Alkohols umgesetzt.
Kann man die Ausbeute noch mehr steigern, wenn man die Essigsäuremenge abermals verdoppelt?
$K=\frac{0,931\frac{mol}{l}*0,931 \frac{mol}{l}}{3,069 \frac{mol}{l}*0,069 \frac{mol}{l}} = 4,12$
Mit Hilfe der Tabellenkalkulation lassen sich die neuen Gleichgewichtskonzentrationen leicht ermitteln. Zwar bleibt von der Essigsäure das meiste unverbraucht über, aber der Alkohol reagiert zu über 93%.
Jetzt wollen wir einmal ausprobieren, was passiert, wenn man nicht die Alkoholkonzentration erhöht, sondern die Essigsäurekonzentration. Mit 4 mol Essigsäure und 1 mol Ethanol erhalten wir das gleiche Ergebnis, nur das jetzt die Konzentration von Essigsäure und Ethanol vertauscht sind: Im Gleichgewicht finden wir nur noch 0,069 mol Essigsäure, dafür aber 3,069 mol Ethanol. Die Ester-Ausbeute liegt immer noch bei 0,931 mol.
Indem man die Konzentration eines Edukts erhöht, kann man das Gleichgewicht der chemischen Reaktion weiter auf die Produktseite verschieben.
Was passiert eigentlich, wenn man beide Edukte in höherer Konzentration reagieren lässt? Probieren wir es aus; wir setzen jetzt 4 mol Essigsäure und 4 mol Ethanol ein.
$K=\frac{2,68\frac{mol}{l}*2,68 \frac{mol}{l}}{1,32 \frac{mol}{l}*1,32 \frac{mol}{l}} = 4,12$
Wir erhalten jetzt zwar mehr Ester, aber die prozentuale Ausbeute bleibt gleich, nämlich 67%. An sich könnte man doch meinen, dass die Hinreaktion wesentlich schneller abläuft als vorher, weil doch die Eduktkonzentrationen so hoch sind. Aber durch die Hinreaktion entsteht jetzt auch wesentlich mehr Produkt, und durch die erhöhte Produktkonzentration verläuft auch die Rückreaktion entsprechend schnell.
Für Computer-Kenner
Am Beispiel der Tabellenkalkulation Numbers (Apple) soll einmal aufgezeigt werden, wie einfach man die Gleichgewichtskonstante K bei gegebenen Gleichgewichtskonzentrationen berechnen kann, wenn man die Gleichung
$A + B \rightarrow C + D$
zu Grunde legt.
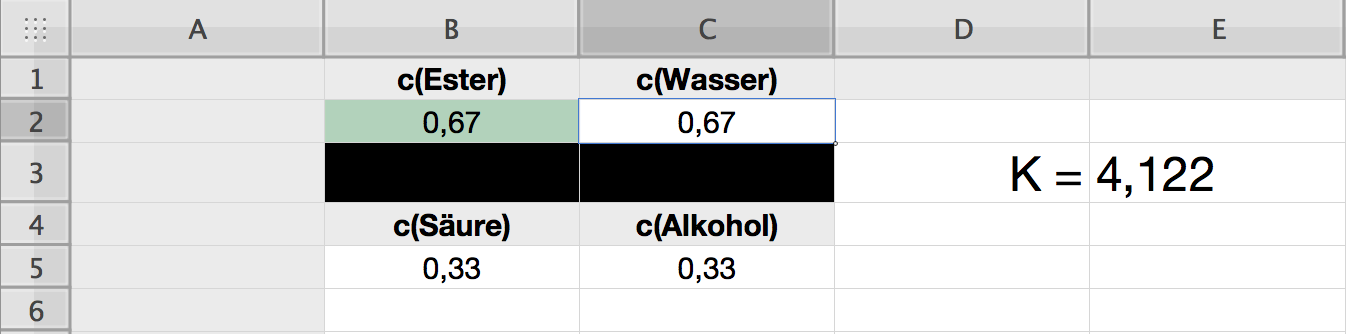
Ein Ausschnitt aus der Tabellenkalkulations-Software Numbers von Apple
In die Zelle B2 tragen wir die Gleichgewichtskonzentration c(Ester) ein, beispielsweise 0,67. Die Einheiten lassen wir hier der Einfachheit wegen weg.
Da laut Reaktionsgleichung immer genau so viel Wasser entsteht wie Ester, tragen wir in die Zelle C2 den gleichen Wert ein. Noch besser: Wir tragen die Formel
$=B2$
in diese Zelle ein. Wenn wir jetzt den Wert von c(Ester) verändern, ändert sich automatisch auch der Wert von c(Wasser).
Die Zellen B3 und C3 wurden hier schwarz gefärbt, um den Bruchstrich in der Gleichung des Massenwirkungsgesetz zu simulieren.
In die Zelle B5 tragen wir den Wert von c(Essigsäure) ein. Wenn wir von 1-molaren Ausgangskonzentrationen ausgehen, können wir auch einfach die Formel
$=1-B2$
in die Zelle B5 eintragen.
In die Zelle C5 können wir entsprechend die Formel
$=B5$
einsetzen. Das gilt natürlich nur für den Fall, dass wir äquimolare Mengen an Säure und Alkohol verwenden. Sollte das nicht der Fall sein, müssen die tatsächlich gemessenen Gleichgewichtskonzentrationen in die Zellen B5 und C5 eingesetzt werden.
In die Zelle E3 kommt nun die etwas komplizierter aussehende Rechenformel:
$=(B2*C2)/(B5*C5)$
Wenn wir nun den Wert des grün hinterlegten Feldes mit der Ester-Konzentration ändern, so ändern sich automatisch auch die Werte der drei anderen Konzentrationen sowie der Wert der Gleichgewichtskonstante K. Hier ein Beispiel:
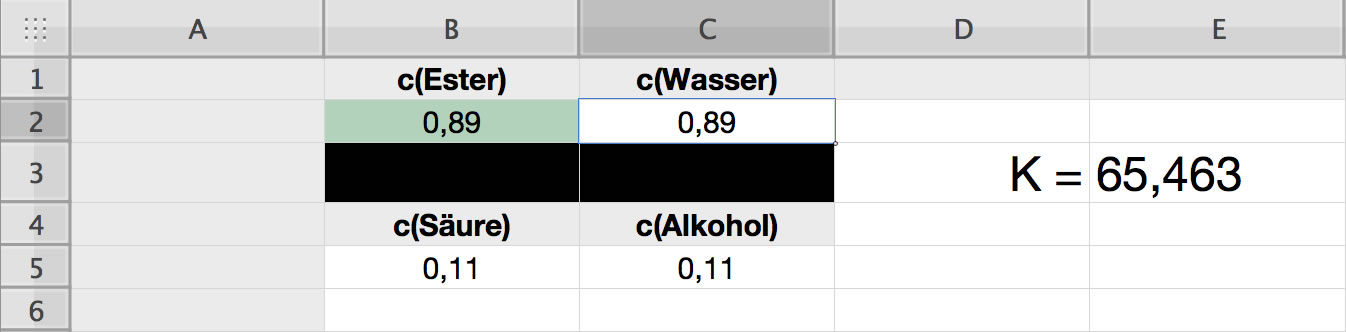
Veränderte Reaktionsbedingungen
Wenn 89% der eingesetzten Säure zum Ester reagieren, steigt die Gleichgewichtskonstante K auf den Wert 65,463 an.
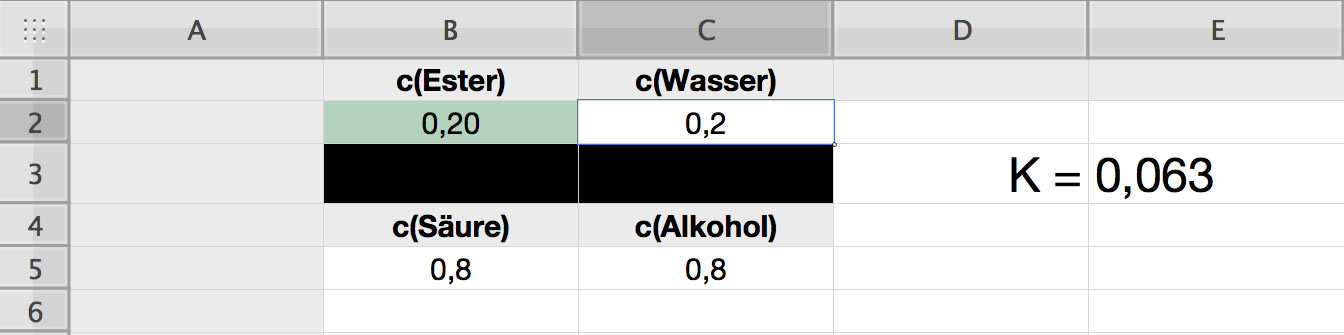
Das chemische Gleichgewicht liegt jetzt auf der linken Seite
Und so würde es aussehen, wenn nur 20% der Säure und des Alkohols zum Ester reagieren würden. Die Gleichgewichtskonstante K hätte dann einen Wert deutlich unter 1.
Aufgabe für Experten:
Machen Sie sich mit Ihrer Tabellenkalkulation vertraut und versuchen Sie, eine ähnliche Simulation zu starten.
Seitenanfang
Weiter mit
dem Prinzip des kleinsten Zwangs...