Hin- und Rückreaktion
Das Massenwirkungsgesetz ist immer wieder ein "Schülerschreck", weil es recht mathematisch ist. Ich versuche jetzt aber mal, das Thema wirklich einfach und eingängig zu erklären, und ich hoffe, dass mir das gelingt.
Bleiben wir bei der Veresterung von Essigsäure mit Ethanol. Hier noch einmal die Reaktionsgleichung:
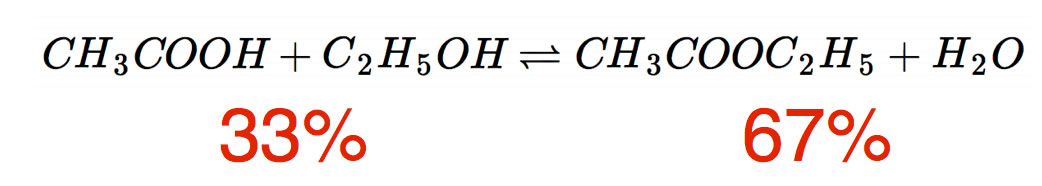
Die roten Zahlen unter den Edukten und Produkten sind so zu lesen: Im Gleichgewichts-Zustand, also wenn sich für den außenstehenden Betrachter nichts mehr ändert, sind 67% der Essigsäure-Moleküle zu Essigsäure-ethylester umgesetzt worden. Das heißt automatisch, dass 33% der Essigsäure-Moleküle und dann natürlich auch 33% der Ethanol-Moleküle nicht an der Reaktion teilgenommen haben.
Bei diesem Gleichgewicht handelt es sich um ein dynamisches Gleichgewicht. Für die außenstehende Betrachterin bleiben die Konzentrationen der beteiligten Edukte und Produkte jetzt konstant. Wenn sie aber genauer hinschauen könnte, würde sie sehen, dass immer noch zahlreiche Essigsäure-Moleküle mit Ethanol-Molekülen zu Ester-Molekülen reagieren, während in der gleichen Zeit genau so viele Ester-Moleküle mit Wasser-Molekülen zusammenstoßen und dabei zu Essigsäure- und Ethanol-Molekülen reagieren.
Vereinfacht kann man dieses dynamische Gleichgewicht auch so formulieren:
$v_{R_{Hin}} = v_{R_{Rueck}}$
wobei $v_{R_{Hin}}$ die Geschwindigkeit der Hinreaktion ist und $v_{R_{Rueck}}$ die Geschwindigkeit der Rückreaktion.
Falls der Browser die Formeln auf dieser Seite nicht richtig darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist der Browser veraltet, oder es besteht im Augenblick keine Internetverbindung.
Die Reaktion von Essigsäure mit Ethanol ist eine sogenannte bimolekulare Reaktion. Es müssen zwei Moleküle zusammenstoßen, damit eine Reaktion stattfindet: Essigsäure-Moleküle müssen mit Ethanol-Molekülen zusammenstoßen.
$Essigsäure + Ethanol \rightarrow Essigsäure-ethylester + Wasser$
Diese Seite habe ich für die Stufe Q1/Q2 geschrieben, die Estersynthese wird hier umfassend in allen Einzelschritten dargestellt. So einfach, wie auf dieser EF-Seite beschrieben, dass nur zwei Moleküle zusammenstoßen müssen, ist es in Wirklichkeit nämlich nicht.
Die Geschwindigkeit einer solchen bimolekularen Reaktion hängt von den Konzentrationen beider Edukte ab. Das ist doch auch irgendwie logisch: Wenn von A nichts vorhanden ist, wenn also c(A) = 0 ist, dann muss vR ebenfalls 0 sein. Genau so ist es mit der Konzentration von B, wenn kein B vorhanden ist, dann muss vR wieder 0 sein. Solche Überlegungen führen dann zu der Gleichung
$v_{R_{Hin}} = k_{Hin} \cdot c(Essigsäure) \cdot c(Ethanol)$
Dabei ist kHin die Geschwindigkeitskonstante der Hinreaktion. Je größer die Geschwindigkeitskonstante kHin ist, desto schneller verläuft die Hinreaktion, in unserem Fall also die Veresterung.
Die Rückreaktion der Estersynthese ist die Esterhydrolyse. Diese Rückreaktion ist ebenfalls eine bimolekulare Reaktion (zumindest bei vereinfachter Betrachtungsweise, die den tatsächlichen Reaktionsmechanismus außer Acht lässt). Wir können diese Rückreaktion allgemein so formulieren:
$Essigsäure-ethylester + Wasser \rightarrow Essigsäure + Ethanol$
Dann gilt für die Reaktionsgeschwindigkeit dieser Rückreaktion:
$v_{R_{Rueck}} = k_{Rueck} \cdot c(Essigsäure-ethylester) \cdot c(Wasser)$
So weit alles klar? Dann kommen wir jetzt mal so langsam zum Massenwirkungsgesetz.
Das Massenwirkungsgesetz
Wir hatten bei der Betrachtung des dynamischen Gleichgewichts der Veresterung festgestellt, dass im Gleichgewichtszustand folgende Beziehung gilt:
$v_{R_{Hin}} = v_{R_{Rueck}}$
Eben haben wir Gleichungen für die Geschwindigkeit der Hin- und die Rückreaktion aufgestellt. Nun verwenden wir diese Gleichungen und setzen sie für vHin und vRück in die obige Formel ein. Dann erhalten wir:
$k_{Hin} \cdot c(A) \cdot c(B) = k_{Rueck} \cdot c(C) \cdot c(D)$
Der bessern Übersicht halber wurde hier mit allgemeinen Abkürzungen gearbeitet. Für unser Beispiel gilt aber: A ist Essigsäure, B ist Ethanol, C ist Essigsäure-ethylester und D ist Wasser.
Bis hierhin sollte eigentlich alles noch verständlich sein; wir haben lediglich vHin und vRück durch die Ausdrücke für die Reaktionsgeschwindigkeit ersetzt.
Nun kommt eine Umformung dieser Gleichung, und zwar wollen wir die beiden Konstanten kHin und kRück auf die linke Seite bringen und alles andere auf die rechte Seite, und dann haben wir eigentlich auch schon das Massenwirkungsgesetz:
$\frac{k_{Hin}}{k_{Rueck}}=\frac{c( C) \cdot c(D)}{c(A) \cdot c(B)}$
Nun stehen auf der linken Seite zwei Konstanten. Wenn man aber eine Konstante durch eine andere dividiert, kommt dabei wieder eine Konstante heraus. Wir können also die Gleichung noch etwas vereinfachen, indem wir eine neue Konstante K einführen und diese dann Gleichgewichtskonstante nennen:
$K=\frac{c( C) \cdot c(D)}{c(A) \cdot c(B)}$
So, das hätten wir geschafft. Viel anfangen können wir mit dem mühsam erarbeiteten Wissen allerdings noch nicht viel. Aber was nicht ist, kann ja noch kommen...
Das Massenwirkungsgesetz und die Estersynthese
Setzen wir nun statt der allgemeinen Symbole A, B, C und D wieder die konkreten Verbindungen ein, die bei der Estersynthese bzw. Esterhydrolyse eine Rolle spielen, dann erhalten wir die Gleichung
$K=\frac{c(Essigsäure-ethylester) \cdot c(Wasser)}{c(Essigsäure) \cdot c(Ethanol)}$
Aus vielen Untersuchungen weiß man, dass bei Zimmertemperatur nur 67% der Essigsäure zum Ester reagiert, dass also 33% der Essigsäure nicht reagiert.
Rechenbeispiel
Wenn man den oben genannten Versuch mit exakt 1 mol Ethanol und 1 mol Essigsäure als Ausgangsstoffe durchführt, dann setzt sich das Stoffgemisch im chemischen Gleichgewichtszustand wie folgt zusammen:
- c(Essigsäure) = 0,33 mol/l
- c(Ethanol) = 0,33 mol/l
- c(Essigsäure-ethylester) = 0,67 mol/l
Auf diese Weise kann man jetzt die Gleichgewichtskonstante K bestimmen:
$K=\frac{0,67 \frac{mol}{l} \cdot 0,67 \frac{mol}{l}}{0,33 \frac{mol}{l} \cdot 0,33 \frac{mol}{l}} = 4,12$
Die Gleichgewichtskonstante $K$ hat hier den Wert 4,12 - ohne eine Einheit. Die Einheiten über und unter dem Bruchstrich kürzen sich hier nämlich gegenseitig heraus. Das muss nicht bei allen Reaktionen so sein, hier ist es aber der Fall.
Wie interpretieren wir nun den Wert 4,2 der Gleichgewichtskonstante $K$?
Ein Wert von $K$ größer als 1 bedeutet doch, dass das Produkt auf dem Bruchstrich größer ist als das Produkt unterhalb des Bruchstrichs. Auf dem Bruchstrich befinden sich die Produkte der Reaktion. Das heißt also, es gibt mehr Produkte als Edukte im Gleichgewicht. Mit anderen Worten: Das chemische Gleichgewicht der Reaktion liegt auf der rechten Seite, der Produktseite. Ein Wert von 4 bedeutet dann, dass das Gleichgewicht schon ziemlich weit auf der rechten Seite liegt. Bei einem Wert von 30 würde das Gleichgewicht noch mehr auf der rechten Seite liegen.
Angenommen, die Gleichgewichtskonzentrationen einer Reaktion
$A + B \rightarrow C + D$
mit den Ausgangskonzentrationen c0(A) = c0(B) = 1 mol/l betragen
- c(A) = c(B) = 0,04 mol/l
- c(C) = c(D) = 0,96 mol/l
Dann hätte die Gleichgewichtskonstante $K$ den Wert
$K=\frac{0,96 \frac{mol}{l} \cdot 0,96 \frac{mol}{l}}{0,04 \frac{mol}{l} \cdot 0,04 \frac{mol}{l}} = 576$
Seitenanfang -
Weiter mit dem Einfluss der Eduktkonzentration...