Schwächen des Kern-Hülle-Modells
Was noch geht...
Kommen wir noch einmal auf die Elektrolyse von Zinkbromid, Magnesiumchlorid oder anderen Salzen zurück, die man an sich gut mit dem THOMSONschen oder dem RUTHERFORDschen Modell erklären kann: An der positiven Elektrode, der Anode, geben die Anionen Elektronen ab, weil
- die Anionen zu viele Elektronen haben und
- an der Anode ein Elektronenmangel herrscht
Die Anionen werden durch die Abgabe der überschüssigen Elektronen wieder zu "normalen" ungeladenen Atomen.
An der negativen Elektrode, der Kathode, nehmen die Kationen Elektronen auf, weil
- die Kationen zu wenige Elektronen haben und
- an der Kathode ein Elektronenüberschuss herrscht
Die Kationen werden durch die Aufnahme der fehlenden Elektronen ebenfalls wieder zu "normalen" ungeladenen Atomen.
All diese Phänomene könnte man gut mit dem Rosinenkuchenmodell von Thomson oder auch dem Kern-Hülle-Modell von Rutherford erklären. Magnesium-Kationen haben zwei Elektronen abgegeben, und sind daher zweifach positiv geladen. Sie werden von einem Minuspol, der Kathode, angezogen. Da dort Elektronenüberschuss herrscht, können die Magnesium-Kationen dort die fehlenden zwei Elektronen aufnehmen und werden wieder zu Magnesium-Atomen.
und was nicht mehr geht...
Was das Kern-Hülle-Modell aber nicht erklären kann, ist die Frage, wieso Magnesium-Ionen überhaupt zweifach positiv geladen sind, während Natrium-Ionen nur einfach positiv geladen sind. Von den dreifach positiv geladenen Aluminium-Ionen ganz zu schweigen.
Auch dass Chlorid-Ionen einfach negativ, Sauerstoff-Ionen aber zweifach negativ geladen sind, kann das Kern-Hülle-Modell nicht erklären.
Auch die Tatsache, dass Edelgase wie Helium oder Neon gar keine Ionen bilden, weder Anionen noch Kationen, ist für das Kern-Hülle-Modell unerklärbar.
Den Begriff der Wertigkeit hatte man damals schon eingeführt. Natrium ist also einwertig, Magnesium zweiwertig, Aluminium dreiwertig, Chlor wieder einwertig, Sauerstoff zweiwertig und so weiter. Mit diesem Wertigkeitskonzept konnte man gut arbeiten und viele quantitative Beobachtungen erklären, zum Beispiel die Summenformeln von Natriumchlorid, Magnesiumchlorid und Aluminiumchlorid NaCl, MgCl2 und AlCl3. Erklären konnte man diese unterschiedlichen Wertigkeiten jedoch nicht mit dem Kern-Hülle-Modell und natürlich erst recht nicht mit dem Rosinenkuchen-Modell oder dem Atommodell von Dalton.
Ein neues, noch besseres Atommodell musste her...
"Beweise" für das Schalenmodell
Betrachten wir einmal ein Schwefel-Atom näher und tun wir so, als stände zufällig eine Apparatur zur Messung von Ionisierungsenergien auf unserem Schreibtisch.
Die Ordnungzahl von Schwefel ist 16; im Atomkern befinden sich also 16 Protonen (und 16 Neutronen), und 16 Elektronen befinden sich in der Elektronenhülle.
Diese Elektronen werden vom Atomkern angezogen. Um ein Elektron aus dem Schwefel-Atom zu entfernen, muss also Energie aufgewandt werden, die sogenannte Ionisierungsenergie.
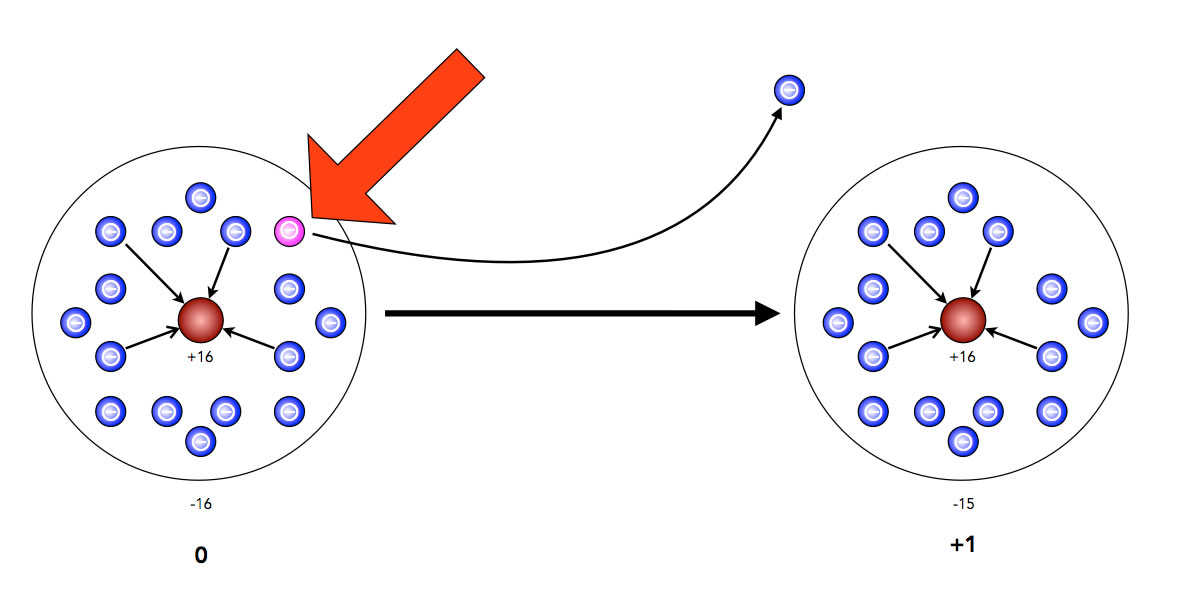
Ionisierung eines Schwefel-Atoms
Autor: Ulrich Helmich 2021, Lizenz: Public domain
Hier sehen wir ein Schwefel-Atom, wie es sich nach dem Kern-Hülle-Modell von Rutherford darstellt. 16 Protonen befinden sich im Atomkern (und 16 Neutronen), und 16 Elektronen halten sich in der Elektronenhülle auf. Nun wird eines der 16 Elektronen durch Energieeinwirkung (roter Pfeil) aus dem Atom herausgeschlagen. Übrig bleiben 15 Elektronen. Da der Atomkern immer noch 16 Protonen besitzt, hat das Atom jetzt eine Gesamtladung von +1 und müsste als Kation bezeichnet werden.
Die für diese Ionisierung erforderliche Energie messen wir jetzt genau, wir haben ja das Gerät zur Messung der Ionisierungsenergie auf unserem Schreibtisch stehen, was für ein Zufall...
Nach der erfolgreichen Versuchsdurchführung überlegen wir, ob wir nicht noch ein zweites Elektron aus dem Schwefel-Atom herausschlagen können. Wir können, es ist tatsächlich möglich. Die dazu erforderliche Energie notieren wir ebenfalls.
Nun werden wir größenwahnsinnig und wollen alle Elektronen auf diese Weise entfernen. Wir führen den Versuch also noch 14 mal durch. Die dazu notwendigen Ionisierungsenergien schreiben wir wieder auf. Und weil wir mit einer Kolonne nackter Zahlen nicht viel anfangen können, stellen wir die Versuchergebnisse, die Messungen der Ionisierungsenergie, einmal graphisch dar:
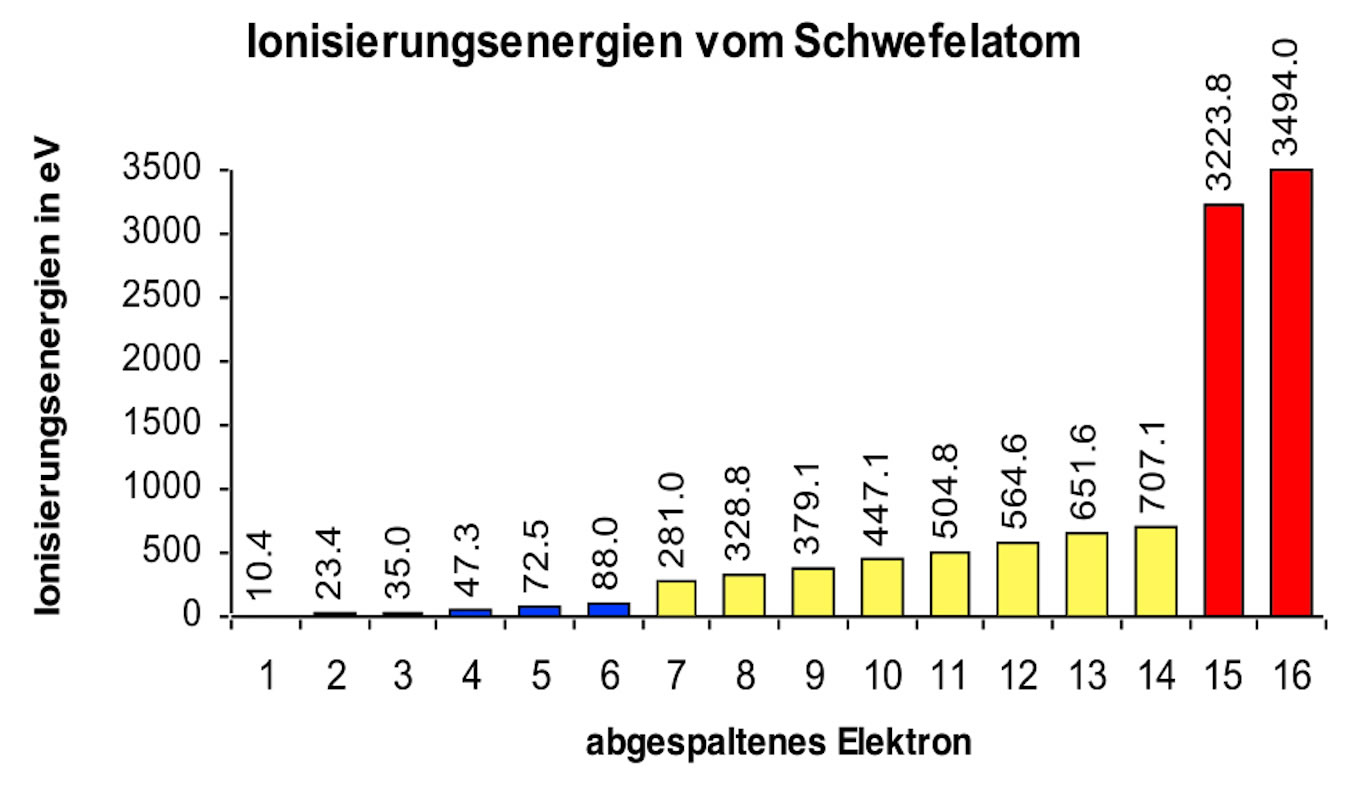
Ionisierungsenergien vom Schwefelatom
Will man nur ein Elektron aus dem Schwefel-Atom entfernen, ist die Ionisierungsenergie noch recht klein (10,4 eV). Das Symbol eV steht übrigens nicht für evangelisch oder eventuell, sondern für Elektronenvolt. Das ist eine Energieeinheit für extrem kleine Energiebeträge, die man mit der Einheit Joule gar nicht mehr vernünftig ausdrücken könnte, weil man dafür zu viele Nullen nach dem Komma bräuchte.
Elektronenvolt
Energieeinheit, die in der Kernphysik bzw. Kernchemie häufig benutzt wird.
Ein Elektronenvolt (1 eV) ist die Energie, die ein Elektron gewinnt, die es beim Durchlaufen einer Beschleunigungsspannung von 1 Volt gewinnt. Dabei gilt:
1 eV = 1,602 * 10-19 J.
Auch für das zweite Elektron braucht man nicht viel mehr Energie (23,4 eV). Genauso für das dritte (35,0 eV), vierte (47,3 eV), fünfte (72,5 eV) und sechste Elektron (88,0 eV). Allerdings steigt der erforderliche Energiebetrag mit jedem Elektron an, das bereits entfernt wurde. Aber dieser Anstieg ist kaum der Rede wert.
Will man jedoch das siebte Elektron entfernen, muss plötzlich sehr viel mehr Ionisierungsenergie aufgewandt werden, nämlich 281,0 eV. Die Elektronen Nr. 8, 9, 10, 11, 12, 13 und 14 erfordern ähnlich viel Energie (bis 707,1 eV); auch hier steigt die Ionisierungsenergie mit jedem entfernten Elektron leicht - aber wirklich nur leicht - an.
Man hat jetzt 14 Elektronen aus dem Schwefel-Atom entfernt. Nun will man das 15. Elektron vom Atom abtrennen. Und der Energiebetrag, der hierfür notwendig ist, ist mit 3223,8 eV noch viel höher als der Betrag für das 14. Elektron. Auch für das letzte Elektron muss man extrem viel Ionisierungsenergie aufwenden (3494,0 eV).
Wie kann man diesen Befund erklären?
Sie haben es schon geahnt: Mit dem Schalenmodell natürlich.
Die Elektronen bewegen sich nicht mehr in einer einheitlichen Kernhülle, sondern auf verschiedenen Bahnen in verschiedenen Abständen vom Atomkern. Die innerste Bahn oder Schale mit dem geringsten Abstand fasst zwei Elektronen. Diese Schale wird als K-Schale bezeichnet. Die nächste Schale, die L-Schale, hat schon einen größeren Abstand zum Atomkern. Auf dieser Schale können acht Elektronen untergebracht werden. Auf der nächsten Schale, der M-Schale, können wieder acht Elektronen untergebracht werden. Diese Schale ist noch weiter vom Atomkern entfernt.
Das Schwefel-Atom sieht nach dem Schalenmodell so aus:
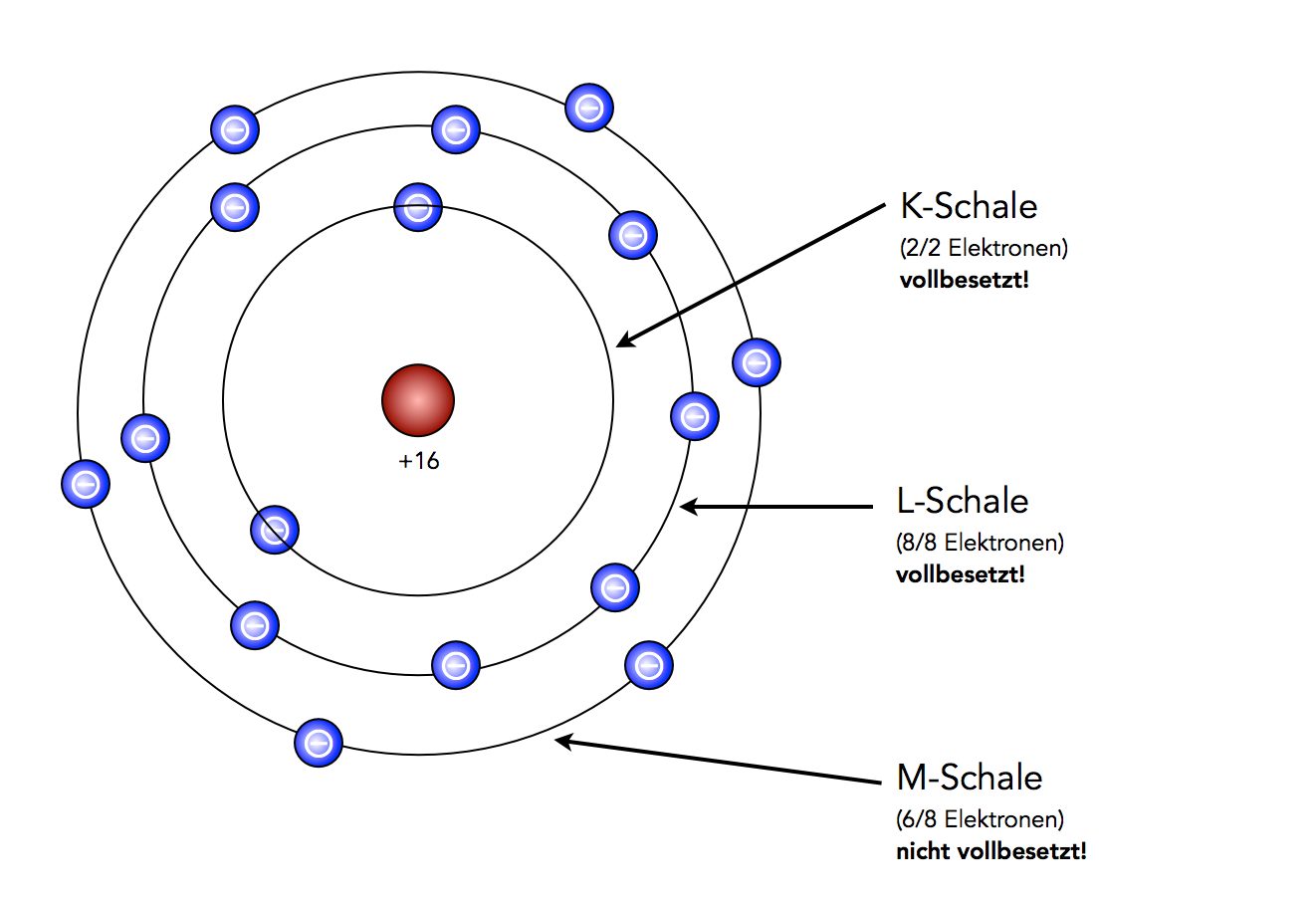
Ein Schwefel-Atom nach dem Schalenmodell
Auf der Skizze sieht man das Schwefel-Atom, wie es sich nach dem Schalenmodell darstellt. Allerdings muss man sich die Schalen räumlich vorstellen, als Kugeln also. Nur lässt sich das nicht so leicht zeichnen, daher die einfachere (und gebräuchlichere) Darstellung.
Auf der äußeren Schale, der M-Schale, befinden sich sechs Elektronen (acht hätten hier Platz). Um diese sechs Elektronen zu entfernen, benötigt man nur eine geringe Ionisierungsenergie. Die Elektronen sind recht weit vom Atomkern entfernt und können daher einigermaßen leicht abgetrennt werden.
Auf der mittleren Schale, der L-Schale, befinden sich acht Elektronen (von maximal acht). Zur Abtrennung dieser acht Elektronen ist schon eine deutlich höhere Ionisierungsenergie erforderlich, da die Anziehungskraft zwischen Atomkern und Elektronen wegen der geringeren Entfernung deutlich größer ist als bei den Elektronen der M-Schale.
Auf der inneren Schale, der K-Schale, befinden sich nur zwei Elektronen. Mehr können auf der K-Schale nicht untergebracht werden. Will man diese beiden Elektronen vom Atom abtrennen, muss man schon sehr viel Ionisierungsenergie aufwenden. Diese beiden Elektronen befinden sich sehr nahe am Atomkern, darum ist die zu überwindende Anziehungskraft sehr groß.
Das Schalen-Modell von Nils Bohr
Das Schalenmodell des Atoms hat der dänische Chemiker Nils Bohr (1885 - 1962) im Jahre 1913 entwickelt hat. Danach besteht ein Atom - genau wie im Kern-Hülle-Modell - aus einer Atomhülle mit den Elektronen und einem Atomkern mit den Protonen (und Neutronen). Allerdings untergliedert sich die Hülle in mehrere Kugelschalen, die eine bestimmte Anzahl von Elektronen aufnehmen können. Die innerste Kugelschale, die K-Schale, kann genau zwei Elektronen aufnehmen, die zweitinnerste Schale, die L-Schale, fasst schon acht Elektronen, die dritte Schale, die M-Schale, bietet 8 Elektronen Platz (und 10 weiteren, aber das ist jetzt zu kompliziert zu erklären) und so weiter.
Das Schalen-Modell
- Alle Aussagen des Kern-Hülle-Modells werden übernommen, allerdings
- besteht die Elektronenhülle aus mehreren Schalen; jede Schale fasst eine bestimmte maximale Anzahl von Elektronen: K-Schale 2, L-Schale 8, M-Schale 18 etc.
- Die äußere Schale enthält die Valenzelektronen, diese können relativ leicht abgegeben werden. So entstehen Kationen.
- Die äußere Schale ist - abgesehen von den Edelgasen - nicht vollständig mit Elektronen besetzt und kann daher weitere Elektronen aufnehmen. So entstehen Anionen.
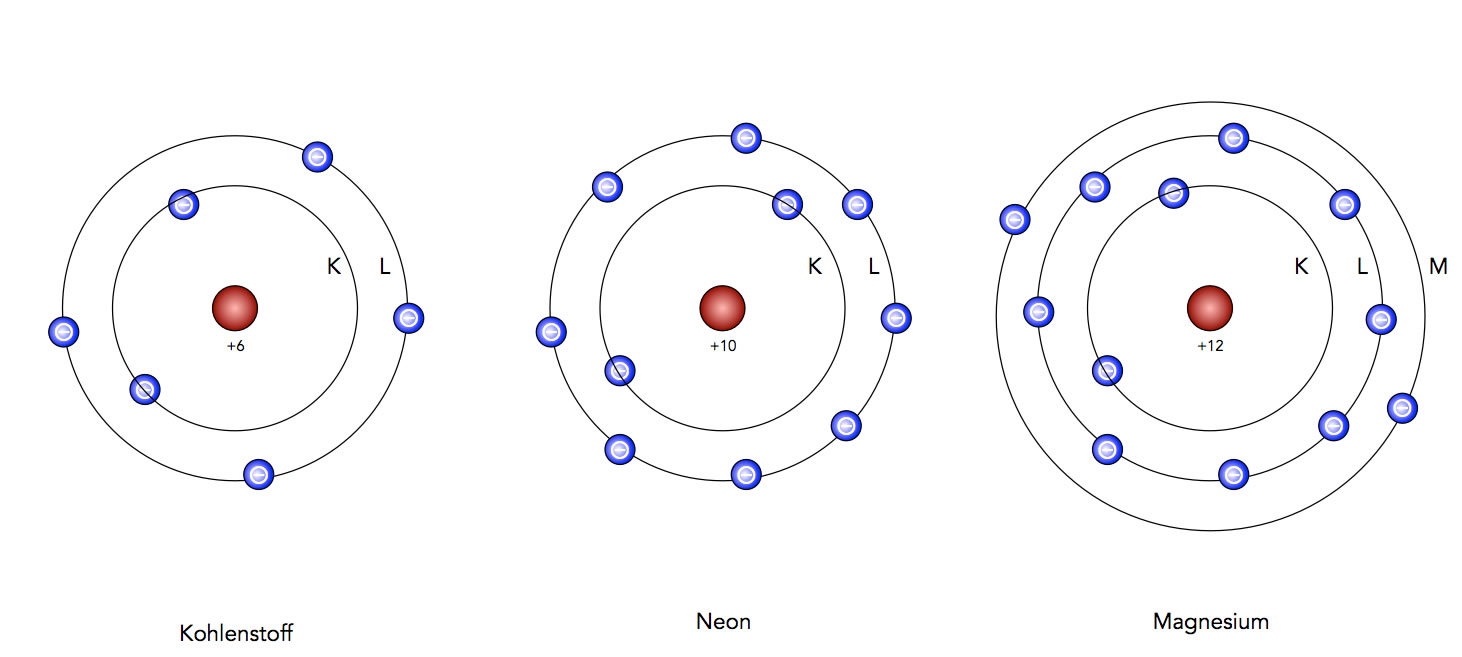
Neon, Magnesium und Chlor nach dem Schalenmodell
Links sehen wir das Modell des Kohlenstoff-Atoms, vereinfacht gezeichnet nach dem Schalen-Modell. Die Vereinfachung besteht darin, dass die Schalen eigentlich nicht kreisförmig sind, sondern kugelförmig, also dreidimensional. Man sieht den Atomkern (die Protonen und Neutronen wurden nicht eingezeichnet) und zwei Schalen. Die K-Schale enthält zwei Elektronen, die L-Schale vier Elektronen. Damit kann man die Vierwertigkeit des C-Atoms leicht erklären: Kohlenstoff kann theoretisch vier Valenzelektronen abgeben, oder Kohlenstoff kann - ebenfalls theoretisch - bis zu vier weitere Elektronen aufnehmen. In Wirklichkeit gibt Kohlenstoff keine Elektronen ab oder nimmt Elektronen auf, aber das wird später erklärt, wenn wir die chemische Bindung behandeln.
In der Mitte sieht man das Neon-Atom. Die beiden Schalen sind voll besetzt. Theoretisch könnte Neon die acht Valenzelektronen abgeben, das wäre aber viel zu energieaufwändig (siehe nächste Abbildung). Weitere Elektronen kann das Neon-Atom nicht aufnehmen. Da Neon Elektronen weder abgeben noch aufnehmen kann, hat es die Wertigkeit 0. Neon kann keine chemischen Verbindungen eingehen (bis auf ganz wenige extreme Ausnahmen).
Ganz rechts ist das Magnesium-Atom nach dem Schalenmodell dargestellt. Die dritte Schale besitzt beim zwei Elektronen, die leicht abgegeben werden können. Daher ist Magnesium zweiwertig. Alternativ könnte Magnesium auch noch sechs weitere Elektronen aufnehmen, das ist aber energetisch sehr ungünstig und damit extrem unwahrscheinlich.
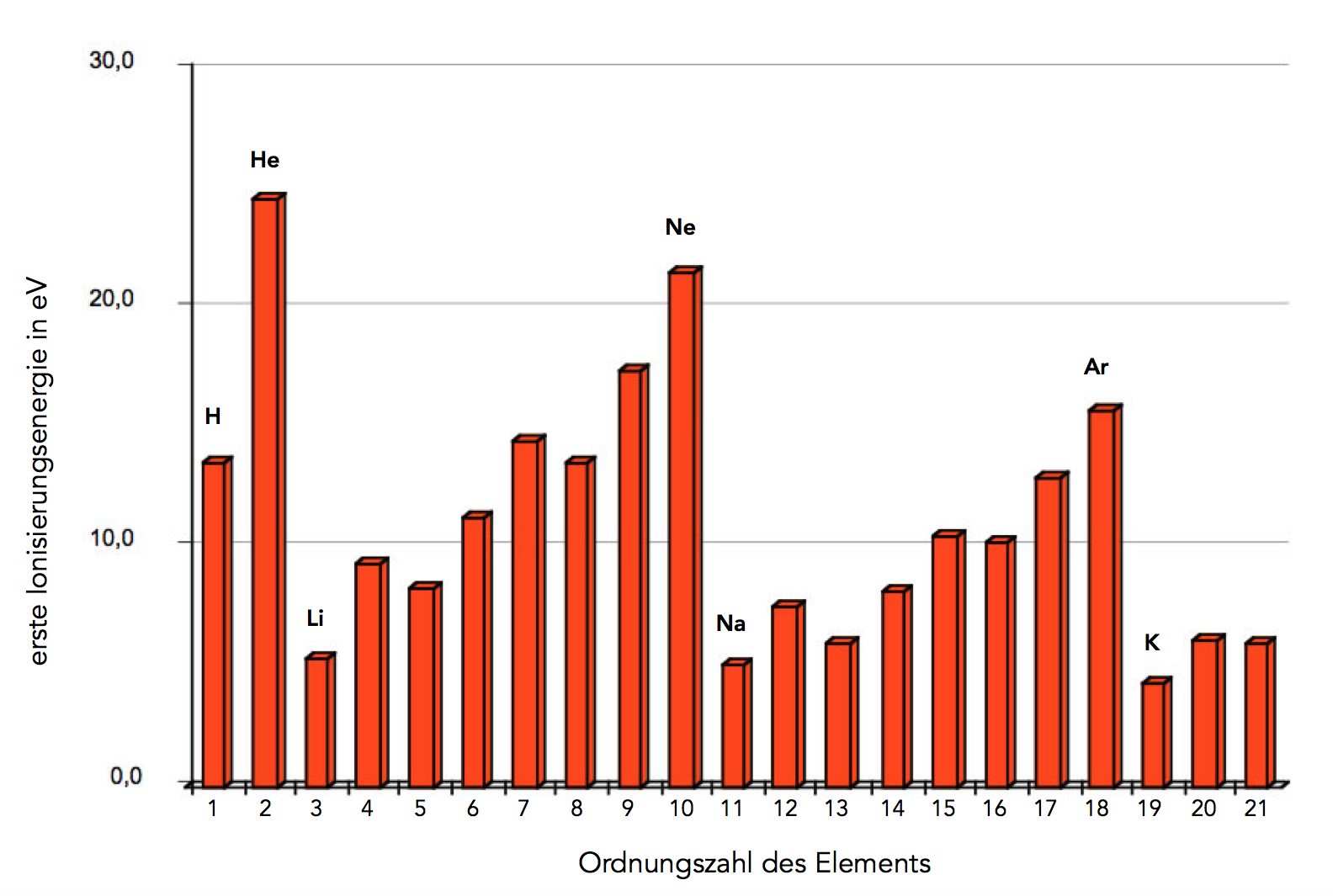
Die Ionisierungsenergien der ersten 21 Elemente
Auf diesem Bild sehen wir die jeweils ersten Ionisierungsenergien für die ersten 21 Elemente, vom Wasserstoff (1) bis zum Scandium (21).
Was sofort auffällt, ist die extrem hohe Ionisierungsenergie der Edelgase (He, Ne, Ar) und die sehr niedrige Ionisierungsenergie der Alkalimetalle (Li, Na, K).
Betrachten wir die Reihe vom Lithium bis zum Neon. Hier steigt die Ionisierungsenergie an, weil die Kernladung immer größer wird. Je größer die Kernladungszahl, desto größer die Kraft, mit der die Elektronen vom Kern angezogen werden, und desto größer der Energieaufwand, um die Elektronen zu entfernen.
Vom Neon zum Natrium beobachten wir einen starken Abfall der Ionisierungsenergie. Das kann man mit dem Schalenmodell gut erklären: Das äußerste Elektron von Natrium-Atomen befindet sich auf der M-Schale, das äußerste Elektron von Neon dagegen auf der weiter innen liegenden L-Schale. Das Neon-Elektron befindet sich also viel näher am Kern als das Natrium-Elektron, daher ist die Anziehungskraft wesentlich geringer. Die Anziehungskraft wird mit dem Quadrat des Abstandes kleiner: Doppelter Abstand = ein Viertel Anziehungskraft, dreifacher Abstand = ein Neuntel Anziehungskraft.
Was man nicht so leicht erklären kann - jedenfalls nicht mit dem Schalenmodell - ist der geringe Abfall der Ionisierungsenergie von Element 4 zu Element 5, von 7 nach 8, von 12 nach 13 und von 15 nach 16. Mit dem Schalenmodell kann man diese Phänomene nicht erklären, mit dem folgenden Modell, dem Kugelwolkenmodell, vielleicht schon etwas besser. Am besten kann man diese Erscheinungen mit dem Orbitalmodell erklären, aber das besprechen wir erst später.
Seitenanfang -
Weiter mit dem Orbitalmodell ...