Auf das Orbitalmodell möchte ich an dieser Stelle noch nicht eingehen, schließlich sind diese Webseiten für Schüler(innen) der Jahrgangsstufe EF bzw. 10 geschrieben. Allerdings werden wir das Orbitalmodell spätestens in der Jahrgangsstufe Q2 bzw. 12 benötigen, wenn Sie das Thema Farbstoffchemie behandeln.
Viele einfache Alltagsphänomene kann man aber nur mit Hilfe des Orbitalmodells erklären, das hätten Sie jetzt nicht gedacht, oder?
Nehmen Sie als Beispiel den Indikator Phenolphthalein. In neutraler Umgebung farblos, wird er in alkalischer Lösung tiefviolett. Diesen Farbumschlag kann keines der bisher bekannten Atommodelle erklären. Das Orbitalmodell dagegen liefert eine Erklärung für dieses Phänomen.
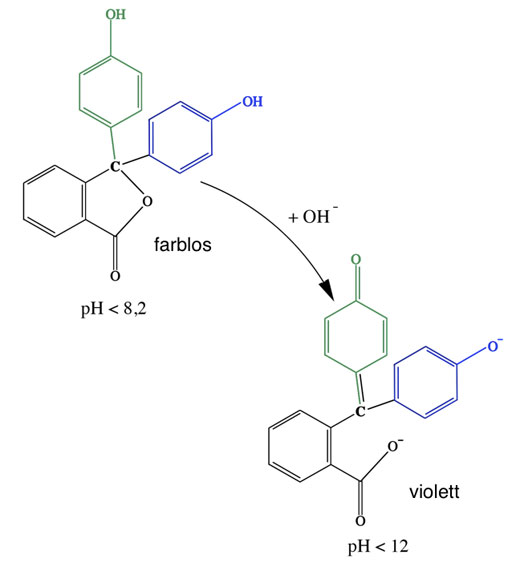
Farbumschlag von Phenolphthalein bei pH >= 8,2
Das mittlere C-Atom des Farbstoffs geht nämlich vom sp3-hybridisierten tetraedrischen Zustand in den sp2-hybridisierten planaren Zustand über, so dass sich die drei aromatischen Ringe des Moleküls zu einem großen aromatischen System zusammenschließen können, in dem der Abstand zwischen bestimmten Molekülorbitalen so klein geworden ist, dass bereits energiearmes sichtbares Licht ausreicht, um die Elektronen anzuregen.
Wenn Sie von dem Gesagten nichts verstanden haben - dann sind Sie hier genau richtig. Solche Sachen sollten Sie auch erst in zwei Jahren verstehen.
Der Vollständigkeit halber möchte ich aber trotzdem einen kurzen Überblick über das Orbitalmodell geben.
Das Orbital-Modell
- Die Aussagen des Schalenmodells werden komplett übernommen, allerdings
- enthält jede Schale jetzt eine bestimmte Anzahl von Orbitalen, die jeweils zwei Elektronen fassen.
K-Schale: 1 x s-Orbital;
L-Schale: 1 x s-Orbital, 3 x p-Orbitale;
M-Schale: 1 x s-Orbital, 3 x p-Orbitale, 5 x d-Orbitale. - Die s-Orbitale sind kugelförmig, die p-Orbitale hantelförmig, die d-Orbitale recht komplex.
Seitenanfang -
Weiter mit dem Kugelwolkenmodell
...