Das Schalenmodell

Das Kern-Hülle-Modell ist recht beschränkt

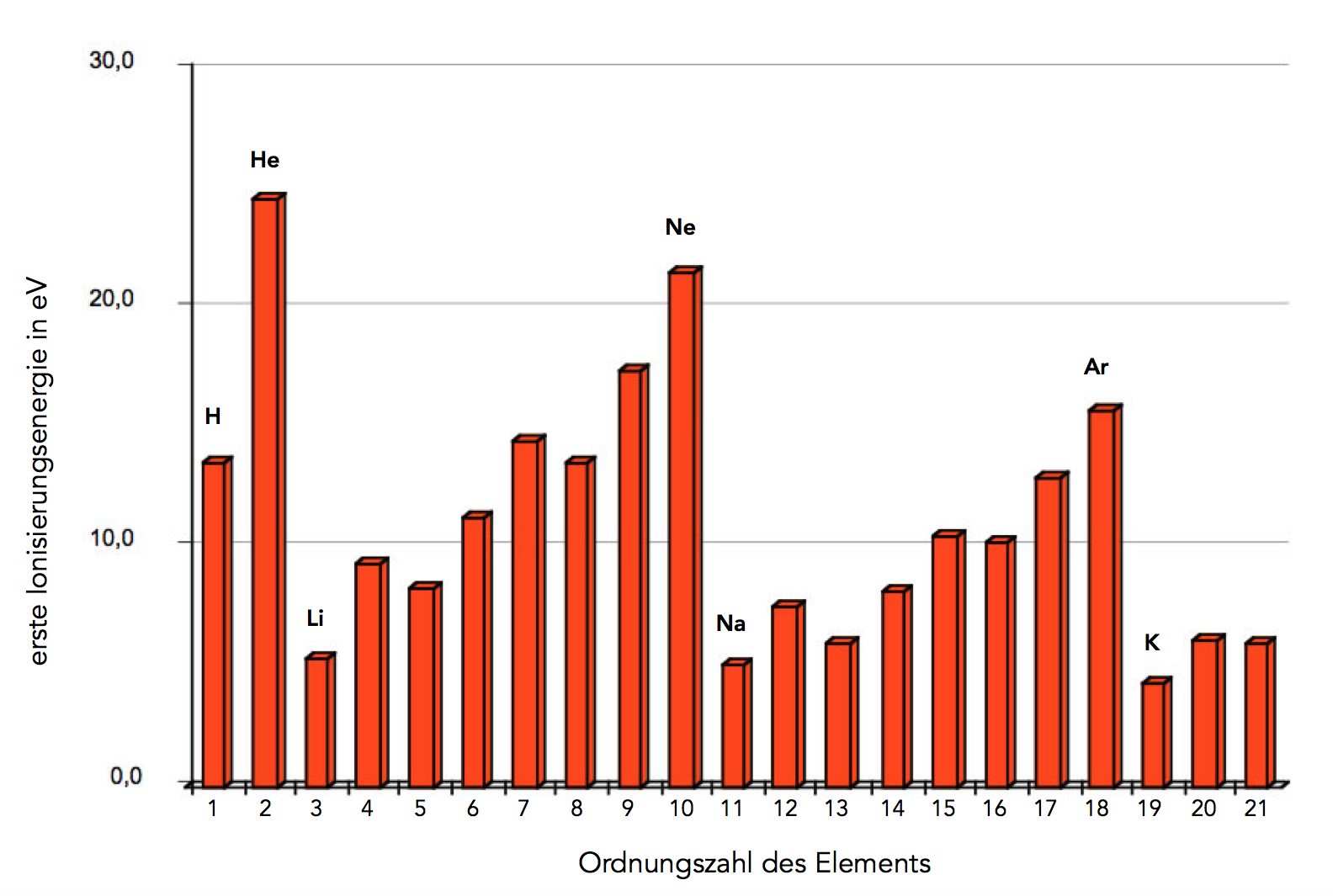
Die Ionisierungsenergien der ersten 21 Elemente

Mit dem Kern-Hülle-Modell können wir schon einige Phänomene erklären, aber längst noch nicht alle. Vor allem kann das Kern-Hülle-Modell von Rutherford nicht das chemische Verhalten der Elemente erklären: Warum sind Natrium und Kalium so äußerst reaktionsfreudig, und warum reagieren die Edelgase überhaupt nicht mit anderen Elementen oder Stoffen?

Was macht ein Chemiker, wenn er mit seinem Atommodell wichtige Phänomene aus Alltag oder Experimente nicht erklären kann? Er fragt eine Chemikerin! Nein, Spaß beiseite: Er oder sie erweitert das Atommodell. Genau das werden wir jetzt mit dem Kern-Hülle-Modell machen, es erweitern.

Ionen und Ionisierungsenergie

Ionen haben wir bereits kennengelernt, nämlich bei der Elektrolyse von Zinkbromid. Mit dem Rosinenkuchenmodell konnten wir die Existenz von Ionen leicht erklären: positive Ionen haben Elektronen abgegeben, negative Ionen haben Elektronen aufgenommen.

Nun geben Atome ihre Elektronen aber nicht einfach so ab. Die Hauptmasse des Atoms, der Atomkern, ist nach dem Kern-Hülle-Modell positiv geladen, während die Elektronen eine negative Ladung tragen. Positive und negative Teilchen ziehen sich aber gegenseitig an. Diese Anziehungskraft muss erst überwunden werden, wenn man ein Elektron von dem Atom abtrennen möchte. Damit wären wir bei einer wichtigen Definition:

Wenn man die ersten 21 Elemente des Periodensystems untersucht und die ermittelten ersten Ionisierungsenergien gegen die Ordnungszahl aufträgt, so erhält man folgende Graphik:

Die Ionisierungsenergien der ersten 21 Elemente

Auf die Maßeinheit, die auf der senkrechten Achse steht, wollen wir hier nicht weiter eingehen. Interessant ist schon die erste Beobachtung: Die Ionisierungsenergie für Helium ist ungefähr doppelt so groß wie die Ionisierungsenergie für Wasserstoff. Das kann man mit der oben dargestellten Formel leicht erklären: Helium-Atome haben einen zweifach positiv geladenen Atomkern, Wasserstoff-Atome nur einen einfach positiv geladenen.

Die Ionisierungsenergie für das Lithium sollte jetzt dreimal so groß sein wie die für Wasserstoff. Diese Erwartung wird aber nicht erfüllt. Im Gegenteil, die Ionisierungsenergie ist nur noch ca. 1/3 so groß wie die von Wasserstoff.

Wie kann man diese wichtige Beobachtung erklären? Dazu müssen wir uns noch einmal die Formel anschauen (die übrigens Coulomb-Formel genannt wird).

$F = k \cdot \frac{L}{r^{2}}$

Offensichtlich spielt hier der Abstand Atomkern - Elektron eine entscheidende Rolle. Es sieht so aus, als ob das erste Elektron, das aus dem Lithium-Atom entfernt wird, einen viel größeren Abstand zum Atomkern hat als das erste (und einzige) Elektron des Wasserstoffs.

Grenzen des Kern-Hülle-Modells

Nach dem Kern-Hülle-Modell befinden sich die Elektronen eines Atoms in der Elektronenhülle. Alle Elektronen sind nach diesem Modell gleichwertig, sie haben den gleichen Abstand zum Atomkern, und sie haben auch den gleichen Energiegehalt.

Diese Behauptung ist nun nicht mehr haltbar. Offensichtlich ist das Elektron des Li-Atoms, das bei der ersten Ionisierung entfernt wird, viel weiter vom Atomkern entfernt als das erste Elektron des Heliums und das einzige Elektron des Wasserstoffs. Das ist aber mit dem Kern-Hülle-Modell nicht mehr vereinbar.

Das Kern-Hülle-Modell hat uns bisher gute Dienste geleistet und reicht auch zur Erklärung vieler Phänomene vollkommen aus. Die unterschiedlichen Ionisierungsenergien kann das Kern-Hülle-Modell allerdings nicht erklären. Das heißt aber nicht, dass dieses Modell falsch ist. Es ist nur unvollkommen. Das ist aber jedes Modell; ein Modell ist immer unvollkommen! Wäre ein Modell nicht unvollkommen, dann wäre es kein Modell mehr, sondern mit dem Original identisch oder zumindest eine exakte Kopie des Originals.

Wie kann man nun das Kern-Hülle-Modell so erweitern, dass die ersten Ionisierungsenergien damit erklärt werden können?

Die Elektronen dürfen nicht mehr alle den gleichen Abstand zum Atomkern haben! Und damit wären wir auch schon beim Schalenmodell angekommen.

Das Schalenmodell

Das Schalenmodell erweitert das Kern-Hülle-Modell um eine wichtige Aussage:

Betrachten wir dazu noch einmal die Abbildung von oben, allerdings leicht ergänzt:

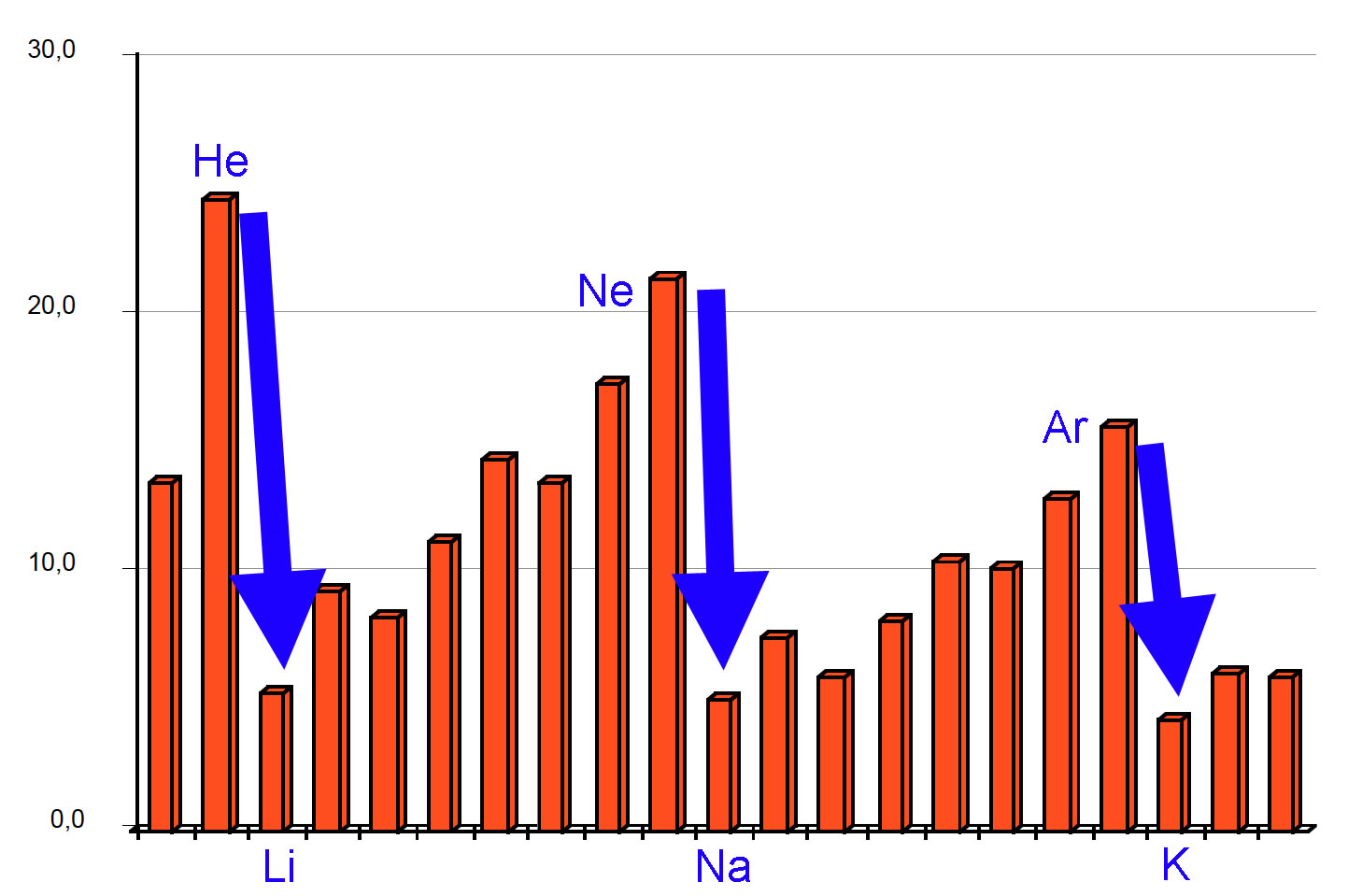
Schlagartige Abnahme der Ionisierungsenergie beim Wechsel der Perioden

Kann man aus dieser Abbildung schon entnehmen, wie viele Elektronen sich auf der K-Schale befinden? Entfernen wir das erste Elektron des H-Atoms, so müssen ca. 13 Energieeinheiten aufgebracht werden. Für das erste Elektron des Heliums ist ungefähr doppelt so viel Energie notwendig, weil der Atomkern die doppelte Ladung trägt.

Dann aber kommt ein großer Sprung in den Ionisierungsenergien. Offensichtlich wird nach dem Helium eine neue Schale "aufgemacht". Die K-Schale fasst also genau zwei Elektronen.

Das Lithium-Atom ist so aufgebaut: Auf der K-Schale befinden sich zwei Elektronen, auf der L-Schale ist dann das dritte Elektron. Bei der Ionisierung wird immer das Elektron entfernt, das am leichtesten zu isolieren ist (Prinzip des geringsten Widerstandes). Wenn also Lithium ionisiert wird, wird nicht eines der beiden K-Elektronen entfernt, sondern das einzige Elektron der L-Schale. Das geht besonders leicht, weil der Abstand zum Atomkern hier besonders groß ist.

Wie viele Elektronen können sich nun maximal auf der L-Schale befinden?

Hier müssen wir einfach nur die Graphik ansehen und schauen, wo der nächste Sprung in den Ionisierungsenergien ist. Der Sprung befindet sich zwischen dem Neon und dem Natrium. Um ein Elektron aus einem Ne-Atom zu entfernen, werden ca. 22 Energieeinheiten benötigt. Wenn man das selbe beim Na-Atom macht, werden nur ca. 5 Energieeinheiten gebraucht. Die L-Schale fasst also 8 Elektronen.

Beim Neon sind die K-Schale mit 2 und die L-Schale mit 8 Elektronen voll besetzt. Beim Natrium kommt noch ein Elektron dazu, das nicht mehr auf die L-Schale passt. Also wird eine neue Schale "aufgemacht", die M-Schale. Das 11. Elektron des Natriums kommt dann auf die M-Schale. Weil hier der Abstand zum Atomkern noch größer ist, kann dieses 11. Elektron jetzt sehr leicht entfernt werden.

Wie viele Elektronen passen auf die M-Schale?

Auch diese Frage können wir jetzt leicht beantworten. Der nächste Sprung in den Ionisierungsenergien taucht vor dem Element Kalium auf. Vom Natrium bis zum Argon sind es wieder 8 Schritte. Die M-Schale fasst also ebenfalls 8 Elektronen. Beim Kalium wird dann eine neue Schale "aufgemacht", die N-Schale.

Ein anderer wichtiger Versuch

Schauen wir uns noch einen weiteren Versuch an:

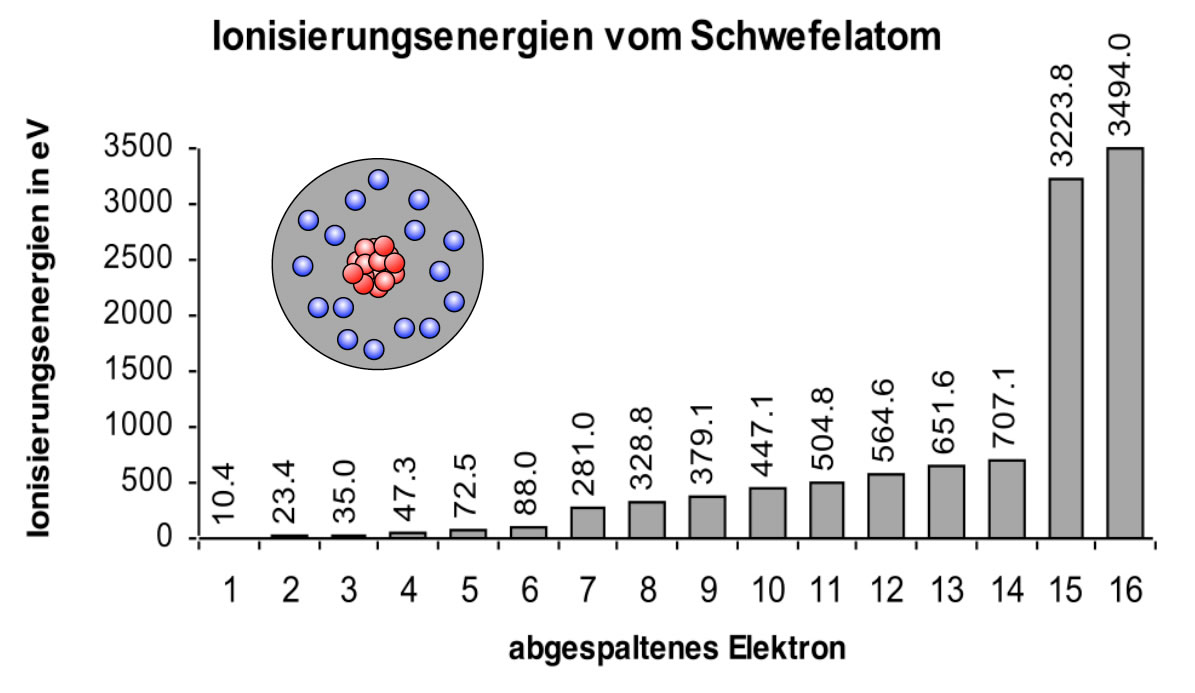
Einem Schwefel-Atom werden nach und nach alle Elektronen entzogen

Was hat man hier gemacht? Ein Schwefel-Atom (16 Elektronen) wurde nach und nach komplett ionisiert. Das Entfernen des ersten Elektrons hat noch nicht besonders viel Energie gekostet. Auch das zweite Elektron lies sich noch recht leicht entfernen, das Gleiche gilt für das 3. bis 6. Elektron. Zwischen dem 6. und dem 7. Elektron gibt es einen deutlichen Sprung, dann steigt die Ionisierungsenergie wieder nur leicht an. Einen noch deutlicheren Sprung gibt es zwischen dem 14. und dem 15. Elektron.

Die Erklärung:

Zuerst werden die Elektronen auf der äußersten Schale des Schwefel-Atoms entfernt. Das geht noch relativ leicht. Bei der Entfernung des 7. Elektrons nimmt die Ionisierungsenergie aber schlagartig zu. Offensichtlich enthält die Außenschale des S-Atoms sechs Elektronen.

Dann werden die Elektronen Nr. 7 bis 14 nach und nach entfernt. Das sind genau acht Elektronen. Also fasst die nächst innere Schale des Schwefel-Atoms genau 8 Elektronen.

Die beiden letzten Elektronen zu entfernen ist sehr energieaufwendig. Nach dem Schalen-Modell, das wir eben kennengelernt haben, handelt es sich hier um die beiden innersten Elektronen auf der K-Schale. Diese beiden Elektronen sind besonders nahe am Kern, darum ist die Anziehungskraft hier extrem hoch.

Damit ist der Aufbau des Schwefel-Atoms klar:

• K-Schale: 2 Elektronen
• L-Schale: 8 Elektronen
• M-Schale: 6 Elektronen

Das Schalenmodell des Atoms, zum zweiten

Nach dem Schalenmodell besteht das Atom aus einem positiv geladenem Atomkern und einer negativen Elektronenhülle. Dabei ist die Elektronenhülle in mehrere Schalen unterteilt. Die drei innersten Schalen sind die K-, die L- und die M-Schale.

1. Auf der K-Schale, der innersten Schale, befinden sich maximal zwei Elektronen.
2. Auf der L-Schale, der zweit innersten Schale, finden maximal acht Elektronen Platz.
3. Auf der M-Schale, der dritten Schale von innen gezählt, haben ebenfalls bis zu acht Elektronen Platz.

Elemente der vierten Periode haben vier Schalen, Element der fünften Periode fünf Schalen und so weiter. Schauen wir uns einfach mal ein paar Atome an, wie man sie nach diesem Schalenmodell zeichnen müsste.

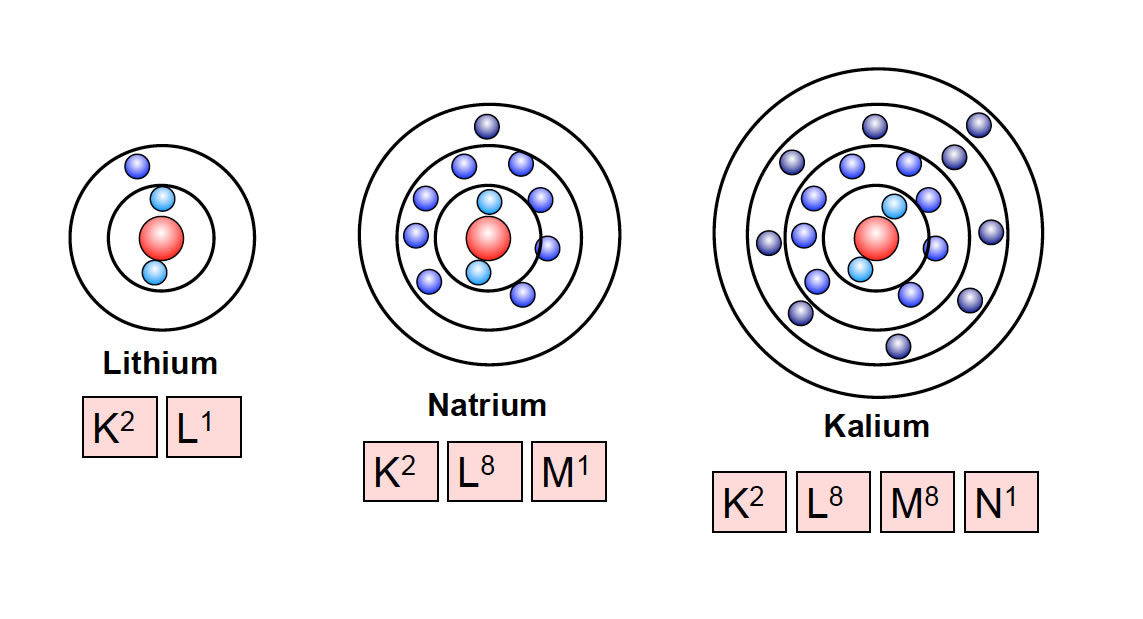
Drei Atome, dargestellt nach dem Schalenmodell">

Auf dieser Abbildung sehen wie die ersten drei Alkalimetalle Lithium, Natrium und Kalium nach dem Schalenmodell. Das Kalium-Atom hat 2 Elektronen auf der K-Schale, 8 Elektronen auf der L-Schale, 8 Elektronen auf der M-Schale und 1 Elektron auf der N-Schale. Wenn man das immer so aufschreiben wollte, wie ich es hier gerade gemacht habe, würde man zu sonst nichts mehr kommen. Daher gibt es eine Kurzfassung dieser Schreibweise, die unter den jeweiligen Atomen zu sehen ist. Diese Kurzfassung wird auch als Elektronenkonfiguration bezeichnet.

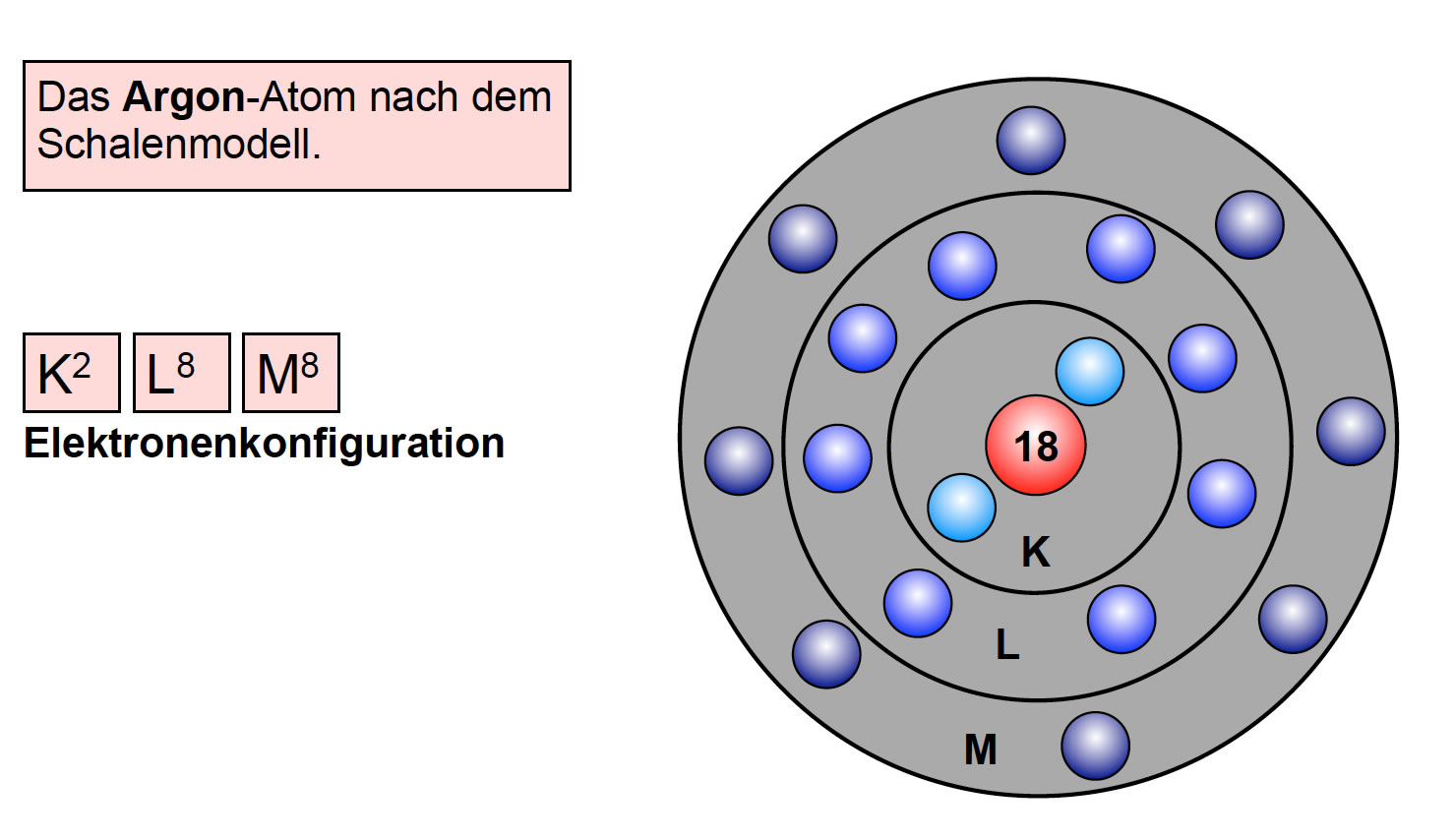
Wie man auf dieser Abbildung gut sehen kann, hat das Argon-Atom 8 Elektronen auf der Außenschale, es hat eine vollbesetzte Außenschale! Das gilt übrigens für alle Edelgase. Auch Helium hat eine vollbesetzte Außenschale. Allerdings hat das Helium-Atom nur zwei Elektronen insgesamt, aber diese befinden sich auf der K-Schale, und die K-Schale fasst maximal 2 Elektronen. Also kann man mit Recht sagen, dass Helium eine vollbesetzte Außenschale hat.

Das Neon-Atom hat die Elektronenkonfiguration K² L⁸ und besitzt damit ebenfalls eine vollbesetzte Außenschale. Und das Krypton-Atom hat die Elektronenkonfiguration K² L⁸ M¹⁸ N⁸ und wieder eine vollbesetzte Außenschale. Die 18 Elektronen auf der M-Schale können wir jetzt noch nicht vernünftig erklären, das geht erst mit dem Orbitalmodell, das in der Jahrgangsstufe 12 (Q2) eingeführt wird.

Grenzen des Schalenmodells

Betrachten wir noch einmal die 1. Ionisierungsenergien der Elemente, achtet jetzt bitte auf die violett markierten Elemente:

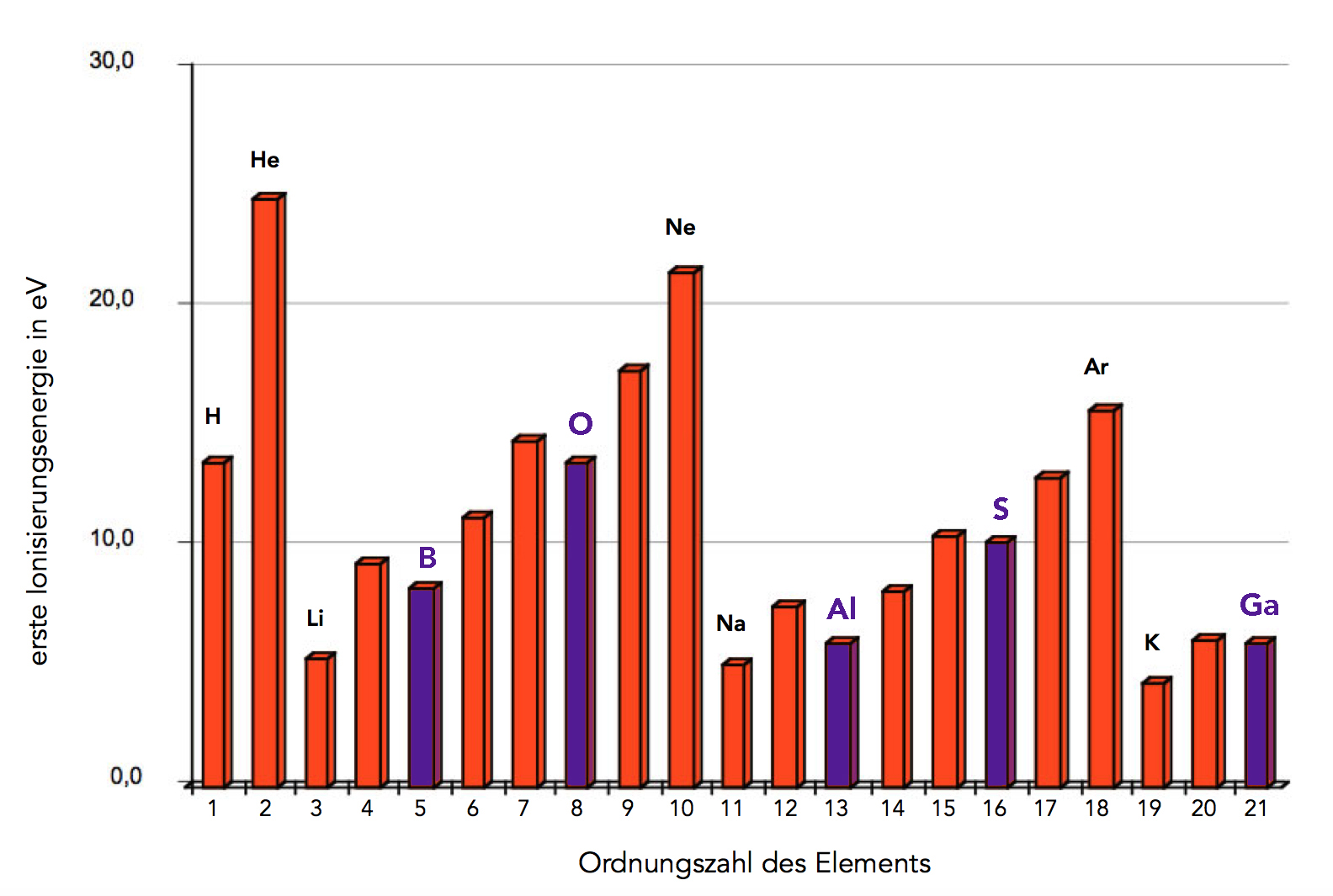
Nicht leicht erklärbare Phänomene bei den Ionisierungsenergien

Bor (Element Nr. 5) hat eine niedrigere 1. Ionisierungsenergie als Beryllium (Element Nr. 4), obwohl doch der Bor-Atomkern fünf Protonen besitzt, der Beryllium-Atomkern aber nur vier. Eigentlich müsste die 1. Ionisierungsenergie von Bor größer sein als die von Beryllium.

Das Gleiche beobachten wir bei Aluminium (Element Nr. 13) und Magnesium (Element Nr. 12). Auch das Gallium (Element Nr. 21) sollte eine höhere 1. Ionisierungsenergie haben als das Calcium (Nr. 20).

Mit dem Schalenmodell kann man diese Unstimmigkeiten nicht erklären. Das heißt aber nicht, dass das Schalenmodell grundsätzlich falsch ist, nur - bedingt durch den Modellcharakter - hat es auch Schwächen und Grenzen, so wie jedes Atommodell, und sei es noch so ausgeklügelt.

Eine Erweiterung des Schalenmodells, mit der man solche Phänomene wie die eben angesprochenen erklären kann, ist das Orbitalmodell. Das ist aber so komplex, dass es erst in der Jahrgangsstufe 12 angesprochen wird (wenn überhaupt). Für das Chemie-Studium sollte man das Orbitalmodell allerdings gut kennen, aber bis dahin sind ja noch ein paar Jahre Zeit.