Gesetz von der Erhaltung der Masse
Mit recht einfachen Versuchen kann man in der Schule nachweisen, dass bei chemischen Reaktionen die Gesamtmasse der beteiligten Stoffe erhalten bleibt. Ganz besonders raffinierte Lehrer zeigen den Schülern zunächst zwei sich widersprechende Versuche:
1. Brennende Kerze:
Eine brennende Kerze wird auf eine hochempfindliche Waage gestellt - und siehe da: die Kerze wird immer leichter.
2. Eisenwolle:
Ein großer Bausch Eisenwolle wird an die linke Seite einer Balkenwaage gehängt, und ein gleich schwerer Bausch Eisenwolle an die rechte, so dass sich die Waage im Gleichgewicht befindet.
Mit dem Bunsenbrenner wird nun der eine Bausch entzündet. Es setzt eine recht heftige Reaktion ein, und man kann sehen, dass der brennende Bausch immer schwerer wird.
Dann wird meistens ein angeregtes Unterrichtsgespräch geführt, in dem die Schüler idealerweise von selbst darauf kommen, dass in dem ersten Versuch ein Stoff entweicht, nämlich Kohlendioxid, während in dem zweiten Versuch etwas aus der Luft aufgenommen wird, nämlich Sauerstoff, und dass man eigentlich die Versuche unter abgeschlossenen Bedingungen durchführen müsste.
Ganz zufällig hat dann der Lehrer schon einen entsprechenden Versuch vorbereitet, und tatsächlich - die Masse der reagierenden Stoffe bleibt erhalten.
Hier sind zwei solcher Versuche:
3. Kupferblech und Schwefel:
In ein Reagenzglas gibt man etwas Kupferblech und ein wenig Schwefel, dann zieht man einen Luftballon über die Reagenzglasöffnung. Als nächstes wird das Reagenzglas inklusive Luftballon gewogen.
Nun erhitzt man das Reagenzglas kräftig, und es kommt zur Reaktion.
Nach erfolgter Reaktion und Abkühlung des Reagenzglases wird erneut gewogen.
4. Salzsäure und Natronlauge:
In einen Erlenmeyerkolben geben wir 100 ml 20%ige Salzsäure. Dann wird der Kolben mit einem Stopfen verschlossen und gewogen. Gleichzeitig wiegt ein anderer Schüler exakt 100g 20%ige Natronlauge ab (100 Gramm und nicht 100 ml; da 20%ige Natronlauge eine etwas höhere Dichte hat als Wasser, ist dieser Unterschied wichtig). Das Gesamtgewicht (Kolben + Salzsäure + Stopfen + 100g Natronlauge) wird notiert.
Dann nimmt man den Stopfen ab, und gibt schnell die 100g Natronlauge in den Erlenmeyerkolben. Sofort wieder den Kolben verschließen und auf die Waage stellen. Es setzt eine Reaktion ein, was man leicht an der Erwärmung des Kolbens merkt. Aber die Masse, die die Waage anzeigt, bleibt konstant.
Es gibt sicherlich noch viele andere Versuche, mit dem man den Massenerhalt zeigen kann; sie alle hier aufzuführen ist sicherlich nicht nötig.
Gesetz von den konstanten Proportionen
Auch hierzu gibt es viele gute Schülerversuche, auf die hier nicht eingegangen werden soll. Stellvertretend soll nur der folgende Versuch beschrieben werden:
5. Kupferblech und Schwefel:
Aus einem dünnen Kupferblech wird ein ca. 5-7 cm langer und 1 cm breiter Streifen geschnitten und so präpariert, dass er in ein Reagenzglas passt. Man kann ihn z.B. zickzackförmig knicken oder zu einer Spirale aufwickeln. Es gibt hier verschiedene Versuchsvorschriften. Wichtig ist, dass der Kupferstreifen genau gewogen wird, bevor er im Reagenzglas verschwindet.
Außerdem gibt man eine Portion Schwefelpulver oder -kristalle in das Reagenzglas. Dann wird kräftig erhitzt, so dass eine Reaktion einsetzt, bei der sich Kupfersulfid bildet. Die Schwefelportion muss natürlich so groß sein, dass das gesamte Kupferblech reagiert.
Nun kommt der schwierigste Teil des Versuchs. Man muss das Reaktionsprodukt aus dem Reagenzglas herausbekommen, ohne dass Teile abbröckeln. Das Kupfersulfid ist nämlich sehr spröde - im Gegensatz zum Kupferblech. Sollten sich noch Reste von Schwefel am Reaktionsprodukt befinden, so sind diese mit einer schwachen Bunsenflamme im Abzug zu verdampfen. Es darf auf keinen Fall zu einer Reaktion des Kupfersulfids mit dem Sauerstoff der Luft kommen.
Nun endlich wird das Reaktionsprodukt gewogen. Jetzt fängt eine mühsame Rechenarbeit an: um wieviel Prozent hat die Masse des Kupferblechs während der Reaktion zugenommen?
Der Versuch wird am besten in Gruppen durchgeführt, so dass man die Ergebnisse der einzelnen Gruppen vergleichen und eventuell einen Durchschnittswert berechnen kann. Im Idealfall (der natürlich nie eintritt) haben alle Gruppen die gleiche Massenzunahme berechnet, und schon kann man im Unterricht das Gesetz der konstanten Proportionen oder Massenverhältnisse an die Tafel schreiben.
Erklärung im Modell
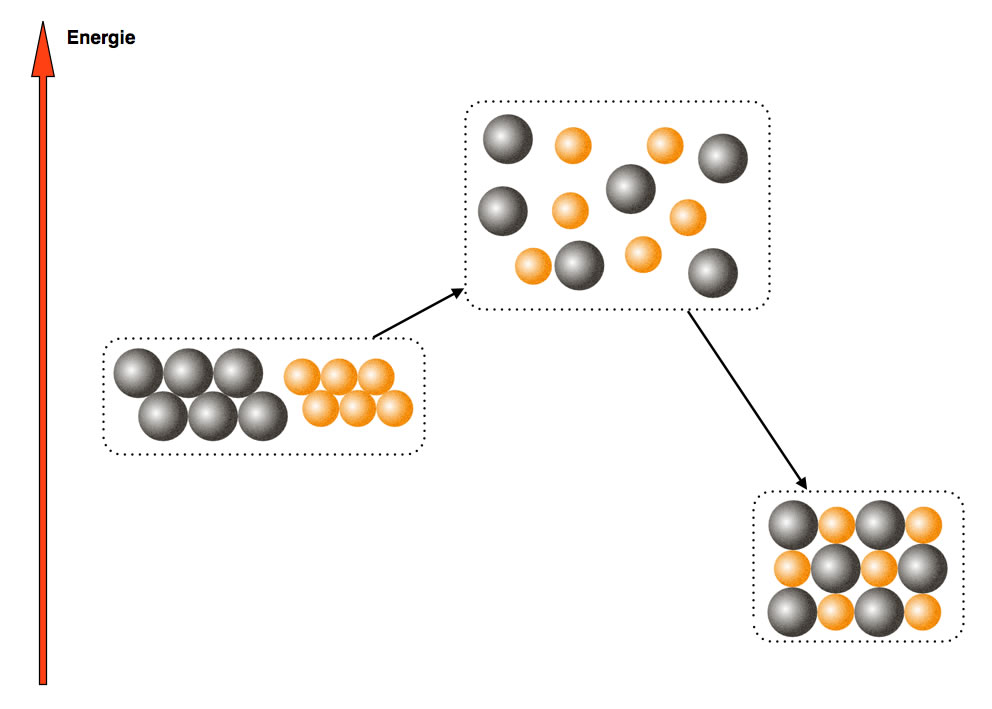
Hier muss man die Atome zählen!
Hier sehen wir noch einmal ein Energiediagramm für die Umsetzung von Eisen mit Schwefel. Dieses Mal liegt der Schwerpunkt aber nicht auf der Energieumsetzung, sondern auf dem Teilchenaspekt.
Wir sehen in der Abbildung sechs Eisen-Atome und sechs Schwefel-Atome. Durch die Zufuhr der Aktivierungsenergie (Erhitzen im Reagenzglas) lösen sich die Atome voneinander und "schwirren durcheinander". Einen solchen Zustand nennt man übrigens Übergangszustand.
Wenn die Teilchen der Ausgangsstoffe den Übergangszustand erreicht haben, vereinigen sie sich auf neue Weise, die neue Verbindung Eisensulfid entsteht. Die Eisen- und Schwefel-Atome gruppieren sich völlig neu, jedes Eisen-Atom ist von mehreren Schwefel-Atomen umgeben, und jedes Schwefel-Atom gleichzeitig von vielen Eisen-Atomen.
Für Experten: Im Eisensulfid liegen Eisen und Schwefel nicht als Atome vor, sondern in Form elektrisch geladener Ionen. Die Eisen-Ionen sind positiv, die Schwefel-Ionen negativ. Das ist der Grund, warum sich die Eisen- und Schwefel-Teilchen im Eisensulfid überhaupt gegenseitig anziehen.
Um die beiden Massengesetze zu erklären, müssen wir uns die Energieveränderungen gar nicht anschauen. Es reicht, wenn wir die Teilchen zählen, also die Atome. Dann merken wir, dass sich die Anzahl der Atome während der Reaktion überhaupt nicht verändert hat. Vor der Reaktion hatten wir sechs Eisen- und sechs-Schwefel-Atome, und nach erfolgter Reaktion zählen wir wieder sechs Eisen- und sechs Schwefel-Atome. Das liegt natürliich daran, dass Atome mit chemischen Mitteln unzerstörbar sind. Es können in einem chemischen Versuch keine neuen Atome entstehen, noch können Atome vernichtet werden. Dazu bedarf es "härterer" Maßnahmen (zum Beispiel Teilchenbeschleuniger, Kernkraftwerk etc.).
Jedes Atom hat eine bestimmte Masse, das hatte man schon im 19. Jahrhunder herausgefunden. Eisen-Atome haben zum Beispiel die Masse 55,8 u. Das Zeichen "u" steht dabei für "unit", das englische Wort für "Einheit" (da hat man es sich aber wirklich leicht gemacht). Schwefel-Atome haben die Masse 32 u, sind also fast halb so leicht wie Eisen-Atome.
Erklärung des ersten Massengesetzes
Wie erklärt man nun das Gesetz von der Erhaltung der Masse? Ganz einfach. Zu Beginn des Versuchs hatten wir sechs Eisen-Atome, jedes davon hat eine Masse von 55,8 u - das runden wir der Einfachheit halber mal auf 56 u auf. Die sechs Atome haben also zusammen eine Masse von 6 * 56 u = 336 u.
Die sechs Schwefel-Atome haben zusammen eine Masse von 6 * 32 = 192 u.
Addieren wir nun die Massen der Eisen- und Schwefel-Atome kommen wir auf 336 u + 192 u = 528 u.
Da sich während der Reaktion die Anzahl der Eisen- und Schwefel-Atome nicht verändert hat und da auch die Atome sich nicht verändert haben, bleibt die Gesamtmasse von 525 u konstant.
Erklärung des zweiten Massengesetzes
Jedes Eisen-Atom verbindet sich während der Reaktion mit genau einem Schwefel-Atom. Schüler, die gut aufgepasst haben, werden jetzt vielleicht sagen: "Moment mal, war es denn nicht so, dass im Eisensulfid jedes Eisen-Atom von vielen Schwefel-Atomen umgeben ist und jedes Schwefel-Atom von vielen Eisen-Atomen?". Dieser Einwand ist völlig richtig, führt aber leider nicht weiter. Denn entscheidend ist das Verhältnis "Zahl der Eisen-Atome" zu "Zahl der Schwefel-Atome". Und dieses Atomzahl-Verhältnis Fe : S ist im Eisensulfid immer 1 : 1.
Da ein Eisen-Atom die Masse von 56 u hat und ein Schwefel-Atom die Masse von 32 u, folgt daraus, dass es eigentlich egal ist, ob sich sechs Eisen-Atome mit sechs Schwefel-Atomen verbinden oder 6000 Eisen-Atome mit 6000 Schwefel-Atomen. Das Verhältnis der Massen bei dieser Reaktion ist immer m(Fe) : m(S) = 56 : 32.
Bei jeder chemischen Reaktion reagieren die Atome der Ausgangsstoffe in einem konstanten Atomzahlverhältnis miteinander (Beispiel Fe : S = 1 : 1). Da jede Atomsorte eine bestimmte Masse hat, resultiert daraus ein konstantes Massenverhältnis (Beispiel Fe : S = 56 : 32).