Aktivierungsenergie
Schauen wir uns mal folgendes Bild an, es zeigt sowohl die Teilchenumsetzungen wie auch gleichzeitig die Energieumsetzungen, die mit der Reaktion von Eisen und Schwefel verbunden sind. Eigentlich kann man diese beiden Aspekte auch nicht voneinander trennen oder sie isoliert betrachten. Beides gehört zusammen.
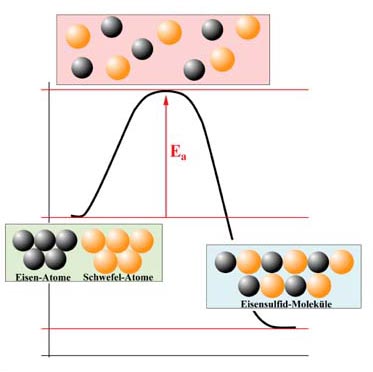
Energiediagramm der Eisensulfid-Bildung
Anmerkung für aufmerksame Leser(innen):
Wie meine nette Kollegin Frau R. Kühn richtig festgestellt hat, ist der Begriff "Eisensulfid-Moleküle" nicht ganz korrekt, aber in der 7. Klasse haben die Schüler nur die Begriffe "Atom" und "Molekül" kennengelernt, der Begriff "Ionenverbindung" ist noch unbekannt.
In Wirklichkeit besteht Eisensulfid aus lauter positiv geladenen Eisen-Ionen und negativ geladenen Sulfid-Ionen, die sich gegenseitig anziehen. Jedes Eisen-Ion zieht mehrere Sulfid-Ionen an, und jedes Sulfid-Ion mehrere Eisen-Ionen. Moleküle in diesem Sinne gibt es also im Eisensulfid nicht.
Eisen und Schwefel befinden sich bei Zimmertemperatur in festem Zustand. Die Atome dieser beiden Elemente ziehen sich also gegenseitig sehr stark an und bilden "dichteste Packungen", wie es für den festen Zustand üblich ist.
Damit Eisen-Atome aber mit Schwefel-Atomen reagieren können, müssen sich alle Atome im Gaszustand befinden, sonst können sie nicht "durcheinanderwirbeln" und miteinander neue Bindungen eingehen.
Die Anziehungskräfte zwischen den Eisen-Atomen einerseits und die Anziehungskräfte zwischen den Schwefel-Atomen andererseits müssen also überwunden werden. Dazu ist Energie notwendig - die Aktivierungsenergie, die oft mit Ea oder EA abgekürzt wird.
Aktivierungsenergie = die Energie, die zugeführt werden muss, damit sich die Teilchen der Ausgangsstoffe voneinander trennen, so dass sie miteinander reagieren können.
Reaktionsenergie
Wir hatten oben gesagt, dass sich die Eisenteilchen im festen Zustand gegenseitig anziehen. Geben wir dieser "Anziehungsenergie" doch einfach mal eine Zahl, zum Beispiel 42. Das heißt, zwei Eisen-Atome ziehen sich mit der Stärke 42 gegenseitig an.
Für Experten: Die Energie, mit der sich zwei Atome eines Moleküls gegenseitig anziehen, wird als Bindungsenergie bezeichnet und in Kilojoule pro Mol gemessen. Ein Mol ist dabei eine bestimmte Anzahl von kleinsten Teilchen, nämlich ungefähr 6 * 1023, eine unvorstellbar große Zahl. Allerdings bildet Eisen keine Moleküle, sondern die Atome eines Metalls sind völlig anderes organisiert, so dass der Begriff Bindungsenergie hier eigentlich nicht zutrifft.
Damit die Eisen-Atome an der Reaktion teilnehmen können, muss die "Bindungsenergie" zwischen den Fe-Atomen also überwunden werden. Dazu muss das Eisenpulver erhitzt werden, damit das Eisen aus dem festen Zustand in den gasförmigen Zustand übergeht.
Für Experten: Die Energie, die einem festen Stoff zugeführt werden muss, damit er gasförmig wird, nennt man Sublimationsenergie.
Das Gleiche gilt für den Schwefel. Auch dieser feste Stoff muss in den gasförmigen Zustand überführt werden, damit die Atome überhaupt reagieren können. Um das Ganze anschaulicher zu gestalten, wählen wir uns wieder irgendeine Zahl aus, die dann die Sublimationsenergie des Schwefels (siehe oben) darstellen soll. Nehmen wir mal... die Zahl 19.
Wir müssen also 42 Einheiten Energie zuführen, um zwei Eisen-Atome zu trennen, und zusätzlich 19 Einheiten Energie, um zwei Schwefel-Atome zu trennen. Das ist ganz schön viel Energie, zusammen also 61 Einheiten.
Zum Trennen von chemischen Bindungen muss immer ein gewisser Energiebetrag aufgewandt werden. Diese "Bindungstrennungsenergie" der Ausgangsstoffe ist hauptverantwortlich für die Aktivierungsenergie einer chemischen Reaktion.
Jetzt wollen wir einmal ein Prinzip anwenden, das ich immer als "Gegenteil-Prinzip" bezeichne: Wenn ich zum Trennen einer chemischen Bindung Energie zuführen muss, was passiert dann, wenn sich eine neue chemische Bindung bildet. Wenn sich also ein Eisen-Atom mit einem Schwefel-Atom verbindet?
Genau: Wenn zum Trennen einer chemischen Bindung Energie verbraucht wird, so müsste nach dem Gegenteil-Prinzip bei der Herstellung einer neuen chemischen Bindung Energie freigesetzt werden.
Jetzt denken wir uns wieder eine Zahl aus, nämlich 38. Fragt bitte nicht, wie ich auf diese Zahl komme, ich habe sie mir gerade eben ausgedacht. Diese Zahl hat absolut nichts mit dem tatsächlichen Energiebetrag zu tun, der bei der Bildung einer Fe-S-Bindung freigesetzt wird.
Bei der Reaktion
$2 Fe_{(s)} + 2 S_{(s)} \to 2 FeS_{(s)}$
werden zwei Eisen-Atome getrennt, dazu ist ein Energiebetrag von 42 erforderlich (die erste ausgedachte Zahl). Außerdem werden zwei Schwefel-Atome getrennt, dazu sind 19 Energieeinheiten erforderlich (die zweite ausgedachte Zahl). Die Aktivierungsenergie für diese Reaktion beträgt demnach 61 Einheiten.
Jetzt bilden sich aber zwei Einheiten Eisensulfid FeS. Als Bindungsenergie für FeS hatte ich mir die Zahl 38 ausgedacht. Da zwei FeS-Einheiten entstehen, werden also insgesamt 76 Energieeinheiten freigesetzt, wenn sich die beiden FeS-Einheiten bilden.
Für Experten: Ich verwende hier nicht den Begriff "FeS-Moleküle", denn das wäre sachlich falsch. Im Eisensulfid-Kristall zieht jedes Eisen-Teilchen mehrere Schwefel-Teilchen an, und umgekehrt zieht jedes Schwefel-Teilchen mehrere Eisen-Teilchen an. Der Begriff "Molekül" würde den falschen Sachverhalt vortäuschen, dass immer genau ein Fe-Atom mit einem S-Atom verbunden ist.
Fassen wir zusammen: Zur Trennung der Fe- und S-Atome mussten wir 61 Energieeinheiten aufwänden, bei der Bildung der FeS-Einheiten werden dagegen 76 Energieeinheiten freigesetzt. Das sind 15 Energieeinheiten mehr, als wir in die Ausgangsstoffe hineinstecken mussten. Das Endprodukt Eisensulfid hat also eine "innere Energie", die 15 Einheiten unter der "inneren Energie" der Ausgangstoffe liegt.
Diesen Energieunterschied zwischen Ausgangsstoffen und Endprodukten bezeichnet man auch als Reaktionsenergie. Mathematisch gesehen ist die Reaktionsenergie die Differenz
Energie der Reaktionsprodukte - Energie der Ausgangsstoffe
Da die Endprodukte energiemäßig 15 Einheiten unter den Ausgangsstoffen liegen, werden bei der Reaktion diese 15 Einheiten an die Umgebung abgegeben. Die Reaktionsenergie dieser Reaktion beträgt also -15 Einheiten.
Die Reaktionsenergie ist der Energieunterschied zwischen der Energie der Endprodukte und der Energie der Ausgangsstoffe. Bei exothermen Reaktionen hat die Reaktionsenergie ein negatives Vorzeichen, bei endothermen Reaktionen dagegen ein positives Vorzeichen. Das liegt daran, dass die Energie der Ausgangsstoffe von der Energie der Endprokte abgezogen wird und nicht umgekehrt.
Anschauliche Darstellung
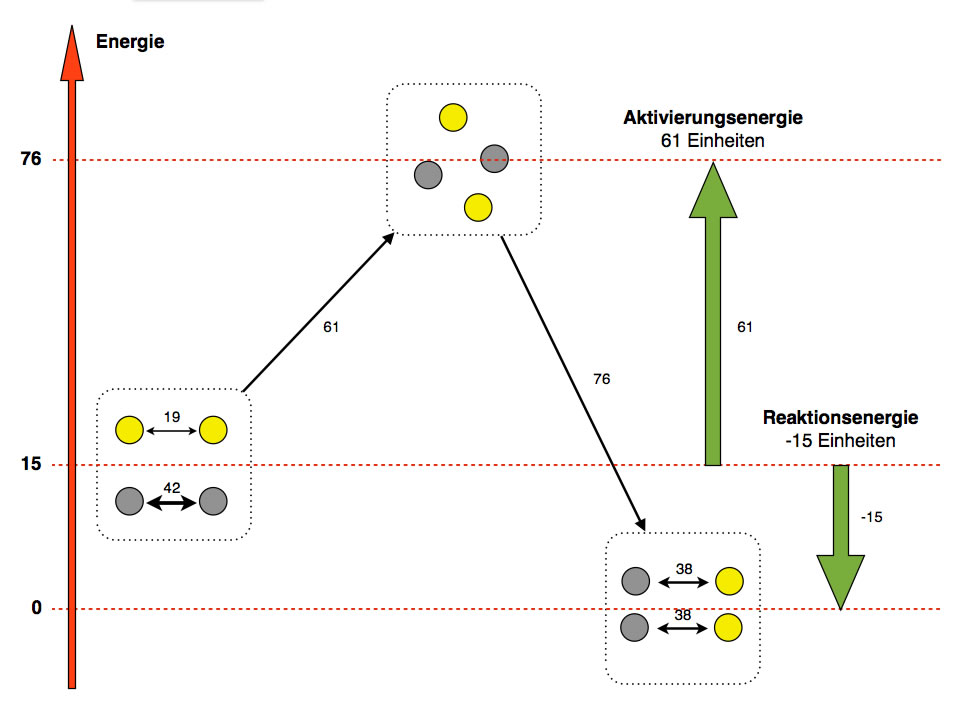
Energiediagramm für die Umsetzung von Eisen mit Schwefel. Willkürlich ausgedachte Zahlen!
Ich habe mal das, was oben im Abschnitt gesagt wurde, anschaulich dargestellt. Zumindest hoffe ich, dass die Abbildung anschaulich ist.
Fangen wir mit der Besprechung der Abbildung links an. Hier sieht man zwei Eisen-Atome (grau), zu deren Trennung 42 Energieeinheiten notwendig sind. Im selben Kasten (Ausgangsstoffe) befinden sich noch zwei Schwefel-Atome (gelb), für deren Trennung nur 19 Einheiten Energie notwendig sind.
Der schräge schwarze Pfeil mit der Zahl 61 verdeutlicht, dass jetzt insgesamt 61 Energieeinheiten in die Ausgangsstoffe hineingesteckt werden müssen, um die Atome voneinander zu trennen. In dem Kasten oben sieht man dann auch die vier Atome, wie sie frei umherschwirren. Der dicke grüne Pfeil rechts veranschaulicht die Aktivierungsenergie für diese Reaktion.
Wenn sich jetzt die Eisen-Atome und die Schwefel-Atome zu Eisensulfid-Einheiten verbinden, entstehen neue Bindungen, und es werden zweimal 38 Einheiten Energie freigesetzt, insgesamt also 76 Einheiten. Das wird durch den schrägen schwarzen Pfeil rechts symbolisiert.
Der rote Pfeil ganz links soll die "innere Energie" der Ausgangsstoffe und der Reaktionsprodukte symbolisieren. Wenn die Ausgangsstoffe eine "innere Energie" von 15 Einheiten haben, dann hat der sogenannte Übergangszustand (Kasten oben) eine "innere Energie" von 15 + 61 = 76 Einheiten, denn zu den 15 Einheiten sind ja noch einmal 61 Einheiten dazugekommen.
Jetzt sind die Ausgangsstoffe "aktiviert" und die Atome können sich neu verbinden. Dabei werden 76 Energieeinheiten freigesetzt. Die "innere Energie" der Reaktionsprodukte liegt also 76 Einheiten unter der Energie des Übergangszustandes und 15 Einheiten unter der Energie der Ausgangsstoffe. Für die "innere Energie" der Produkte habe ich in dieser Graphik einfach mal willkürlich den Wert 0 gewählt, das sieht irgendwie besser aus als ein "krummer" Wert wie 45 oder so.
Frage für Experten: Angenommen, man könnte die "innere Energie" der Produkte tatsächlich messen und käme auf einen Wert von 45. Welche "innere Energie" hätten dann die Ausgangsstoffe? Ganz einfach: 45 + 15 = 60. Und welche "innere Energie" hätte dann der Übergangszustand? Auch wieder ganz einfach, nämlich 60 + 61 = 121.
Kommen wir jetzt noch einmal zum Begriff der Reaktionsenergie. Das ist ja die Differenz zwischen der Energie der Endprodukte und der Energie der Ausgangsstoffe. Mit Hilfe der Abbildung ist es jetzt gar kein Problem, diesen Wert für die Reaktionsenergie zu berechnen. Die Energie der Endprodukte beträgt 0 Einheiten, die der Ausgangsstoffe 15 Einheiten. Wir müssen also 0 - 15 rechnen und kommen auf die negative Zahl -15. Die Reaktionsenergie beträgt also -15 Einheiten.
Für Experten: Diese Zahlen sind alle willkürlich ausgedacht. In Wirklichkeit kann man die "innere Energie" eines Stoffes nicht messen. Was man messen kann, sind Energieunterschiede. Man kann also feststellen, wie hoch die Aktivierungenergie für eine Reaktion ist, und man kann messen, wie viel Energie bei einer Reaktion insgesamt freigesetzt wird, so dass man die Reaktionsenergie berechnen kann. Man könnte natürlich ein künstliches Bezugssystem erfinden und zum Beispiel sagen: Wir setzen die innere Energie von flüssigem Wasser einfach auf den willkürlichen Wert 0, dann kann man leicht die inneren Energien anderer Stoffe wie Eisen oder Schwefel angeben. Das wäre natürlich eine Möglichkeit, die aber, so weit ich weiß, (noch) nicht realisiert worden ist.