Grundlegendes
Ein Baum kann theoretisch völlig ungeordnet, sogar chaotisch aufgebaut sein. Solange jeder Knoten mindestens zwei Nachfolger hat, handelt es sich um einen Baum. In der Definition des Begriffs "Baum" steht nicht, wie diese Nachfolger angeordnet sein müssen oder dass sie überhaupt geordnet sein müssen.
In der Informatik sind solche ungeordneten Bäume in der Regel nutzlos. Bäume dienen meistens zum Speichern von Daten, und Daten will man möglichst schnell wiederfinden. Daher muss ein Baum geordnet sein. Das erreicht man mit Hilfe einer bestimmten Klasse von Bäumen, den sogenannten Suchbäumen.
Im Informatik-Abitur (NRW) spielen vor allem binäre Suchbäume eine wichtige Rolle. Ein binärer Suchbaum ist ein Suchbaum, bei dem jeder Knoten exakt zwei Nachfolger hat (die aber beide leer sein können).
Die folgende Abbildung zeigt einen solchen binären Suchbaum:
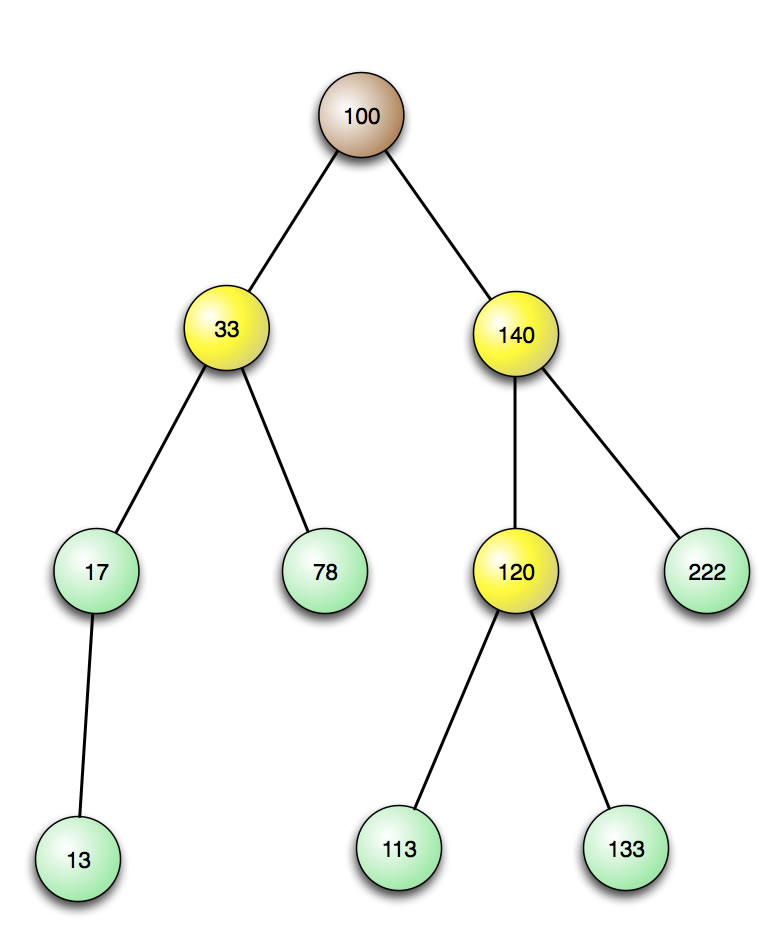
Ein binärer Suchbaum
Autor: Ulrich Helmich 2018, Lizenz: CC BY-NC-SA 4.0
Die Wurzel enthält als Inhalt die Zahl 100. Alle Knoten links von der Wurzel haben kleinere Zahlen als Inhalt, alle Knoten rechts der Wurzel dagegen Zahlen, die nicht kleiner sind (also gleich oder größer). Diese Regel gilt auch für jeden der inneren Knoten. Schauen wir uns beispielsweise den Knoten 33 an. Der linke Nachfolger hat einen kleineren Wert (17), der rechte Nachfolger einen größeren Wert (78).
Nach dieser Vorbetrachtung sollte die Definition des Begriffs "binärer Suchbaum" eigentlich kein Problem mehr sein:
binärer Suchbaum
Ein binärer Suchbaum ist ein Binärbaum, bei dem für alle Unterbäume gilt:
- der linke Unterbaum eines Knotens enthält nur Elemente, deren Wert kleiner als der Wert des Knotens ist.
- der rechte Unterbaum eines Knotens enthält nur Elemente, deren Wert nicht kleiner als der Wert des Knotens ist.
Binäre Suchbäume als ADTs
Übrigens ist ein binärer Baum ein Abstrakter Datentyp (ADT), denn er kann allein durch Angabe seiner Operationen definiert werden. Hier ein mögliches Beispiel für eine Definition des ADT "Binärer Suchbaum":
Der ADT Binary Tree
Der Abstrakte Datentyp binärer Suchbaum wird durch folgende Operationen definiert:
- Init(): Erzeugt einen leeren Suchbaum.
- Insert(x): Das Element x wird hinzugefügt, und zwar in den linken Unterbaum, wenn es kleiner ist als die Wurzel, ansonsten in den rechten Unterbaum.
- Remove(x): Das Element x wird entfernt, falls es vorhanden ist.
- Member(x): Falls das Element x im Baum vorhanden ist, wird TRUE zurückgeliefert, ansonsten FALSE.
- Empty(): Falls der Binärbaum leer ist, wird TRUE zurückgeliefert, sonst FALSE.
Natürlich kann man weitere Operationen in diese Definition aufnehmen, zum Beispiel könnte man Operationen entwerfen, die den linken bzw. rechten Teilbaum der Wurzel als Wert zurückliefern und so weiter.
Im Informatik-Abitur (NRW) werden binäre Suchbäume meistens nicht als ADT behandelt, sondern als eine konkrete Java-Klasse BinarySearchTree.
Vorteil binärer Suchbäume
Welche Vorteile hat nun ein solcher binärer Suchbaum gegenüber einer doppelt verketteten sortierten Liste von Elementen? Schauen wir uns dazu eine konkrete Liste an. Auf die Wiedergabe der Zeiger wurde hier aus Übersichtsgründen verzichtet.

Eine sortierte Liste von Zahlen
Autor: Ulrich Helmich 2018, Lizenz: CC BY-NC-SA 4.0
Das Element 78 soll durch eine lineare Suche gefunden werden. Dazu sind vier Vergleiche notwendig, wie man unschwer erkennen kann. Die gleiche Suche in unserem binären Suchbaum aus der Abbildung oben würde nur drei Vergleiche kosten. Um das Element 100 in der Liste zu finden, wären bei einer linearen Suche fünf Vergleiche notwendig. In dem Suchbaum finden wir die 100 bereits nach einem Vergleich, denn die 100 ist ja die Wurzel des Baums.
Man erkennt sofort, dass das Suchen in dem Binärbaum im Durchschnitt viel schneller geht als in einer sortierten Liste.
Für Experten
Hier könnte man natürlich einwenden: Würde man die sortierte Liste mit einem binären Verfahren durchsuchen, so ginge das genau so schnell wie das Durchsuchen eines Binärbaums.
Dieser Einwand ist berechtigt, allerdings ist das binäre Suchen ja auch eine Methode, bei der man eine sortierte Liste quasi vorübergehend in einen binären Suchbaum verwandelt. Man macht sich also die gleiche Technik zu Nutze, die auch in einem binären Suchbaum steckt.
Schauen wir uns nun folgenden Binärbaum an:
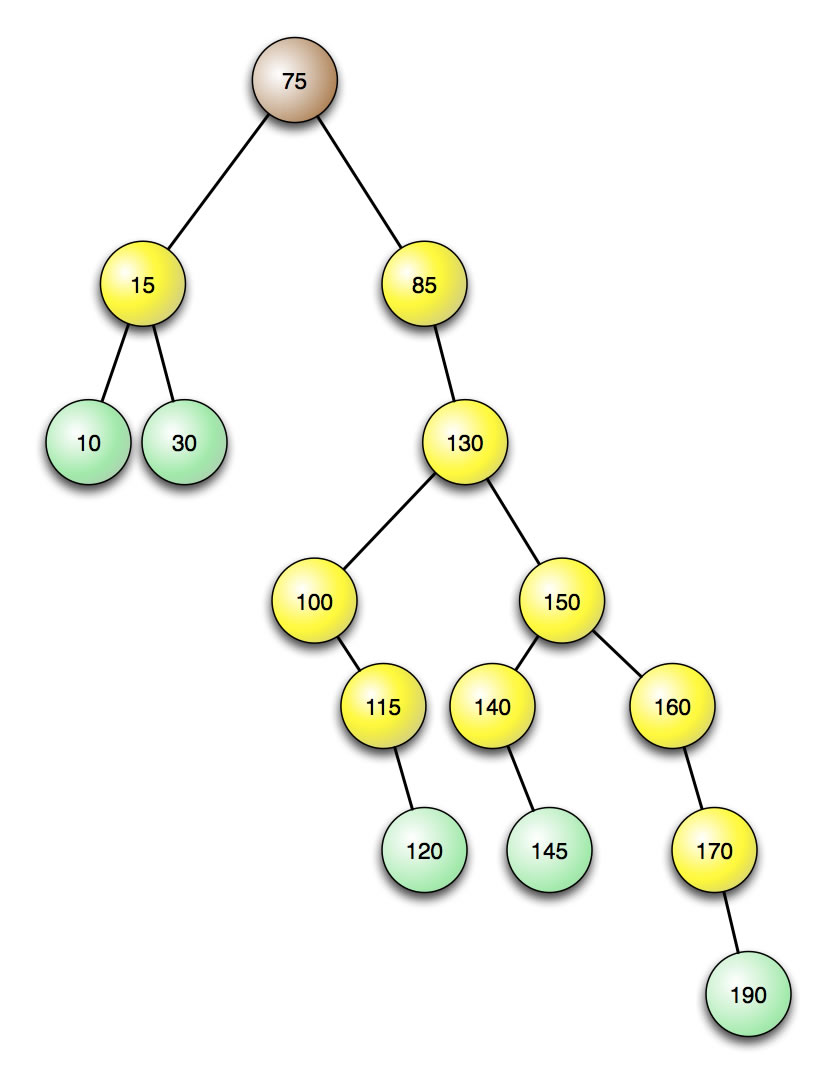
Ein sehr rechtslastiger Binärbaum
Autor: Ulrich Helmich 2018, Lizenz: CC BY-NC-SA 4.0
Die 15 Zahlen sind geordnet untergebracht; alle Zahlen des jeweils linken Teilbaums sind kleiner als die Zahl in der Wurzel, und die nicht-kleineren Zahlen befinden sich jeweils im rechten Teilbaum. Jeder Knoten hat maximal zwei Nachfolger, und damit sind alle Bedingungen für einen binären Suchbaum erfüllt. Allerdings ist dieser Baum nicht optimal aufgebaut. Zum Finden der Zahl 190 beispielsweise benötigt man 7 Vergleiche, weil sich die 190 in der 7. Ebene des Baumes befindet. Zum Finden der 10 dagegen werden nur 3 Vergleiche benötigt. Rechnet man alles zusammen:
1x1 + 2x2 + 3x3 + 2x4 + 3x5 + 3x6 + 1x7 = 62
und teilt die Summe der benötigten Vergleiche, um alle Zahlen zu finden, durch die Anzahl der Zahlen, also 14, so erhält man 62/15 = 4,13 Vergleiche im Schnitt. Um eine (vorhandene) Zahl in diesem Baum zu finden, sind also im Schnitt 4,13 Vergleiche notwendig.
Der folgende binäre Suchbaum
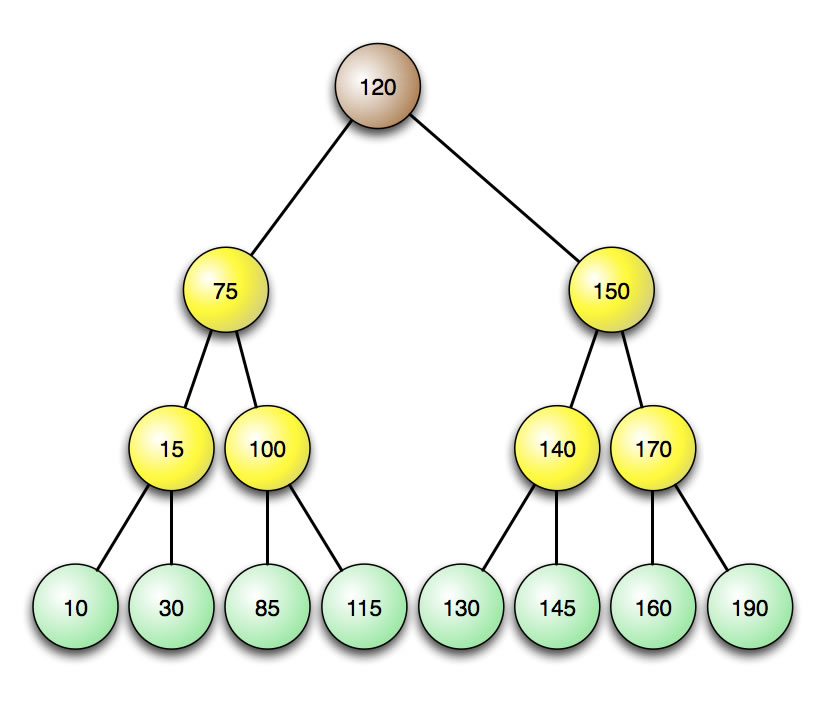
Ein vollständig ausgeglichener Binärbaum
Autor: Ulrich Helmich 2018, Lizenz: CC BY-NC-SA 4.0
enthält die gleichen 15 Zahlen. Allerdings ist dieser binäre Suchbaum optimal aufgebaut, er ist vollständig ausgeglichen. Maximal 4 Vergleiche sind zum Auffinden einer Zahl notwendig. Die genaue Berechnung liefert
1x1 + 2x2 + 4x3 + 8x4 = 49
Um hier eine Zahl zu finden, sind also 49/15 = 3,27 Vergleiche notwendig. Das ist schon ein großer Fortschritt gegenüber dem nicht-ausgeglichenen Baum, und ein riesengroßer Fortschritt gegenüber einer sortierten linearen Liste; hierfür wären bei 15 Zahlen ca. 7,5 Vergleiche im Schnitt notwendig.
Für Experten:
Das Zeitverhalten des Suchens in einem binären Suchbaum kann durch die Formel
O(N) = log N
charakterisiert werden.
Begründung:
Ein vollbesetzter binärer Suchbaum mit zwei Ebenen hat drei Knoten:
20 + 21 = 3
Ein vollbesetzter binärer Suchbaum mit drei Ebenen hat sieben Knoten:
20 + 21 + 22= 7
Um die sieben Zahlen in dem vollbesetzten Baum mit drei Ebenen zu finden, sind maximal 3 Vergleiche notwendig. Nun ist log2(8) = 3 bzw. log2(7) < 3. Und für die drei Zahlen in den Ebenen 1 und 2 sind sogar noch weniger Vergleiche notwendig. Also trifft die Behauptung O(N) = log N durchaus zu.
Seitenanfang -
Weiter mit der Implementation eines binären Suchbaums...