Populationswachstum der Beute
Bereits im Abschnitt "Demökologie" haben wir die Differentialgleichung für das Wachstum einer Population kennengelernt. Schauen wir uns diese Gleichung für eine Beutepopulation noch einmal näher an:
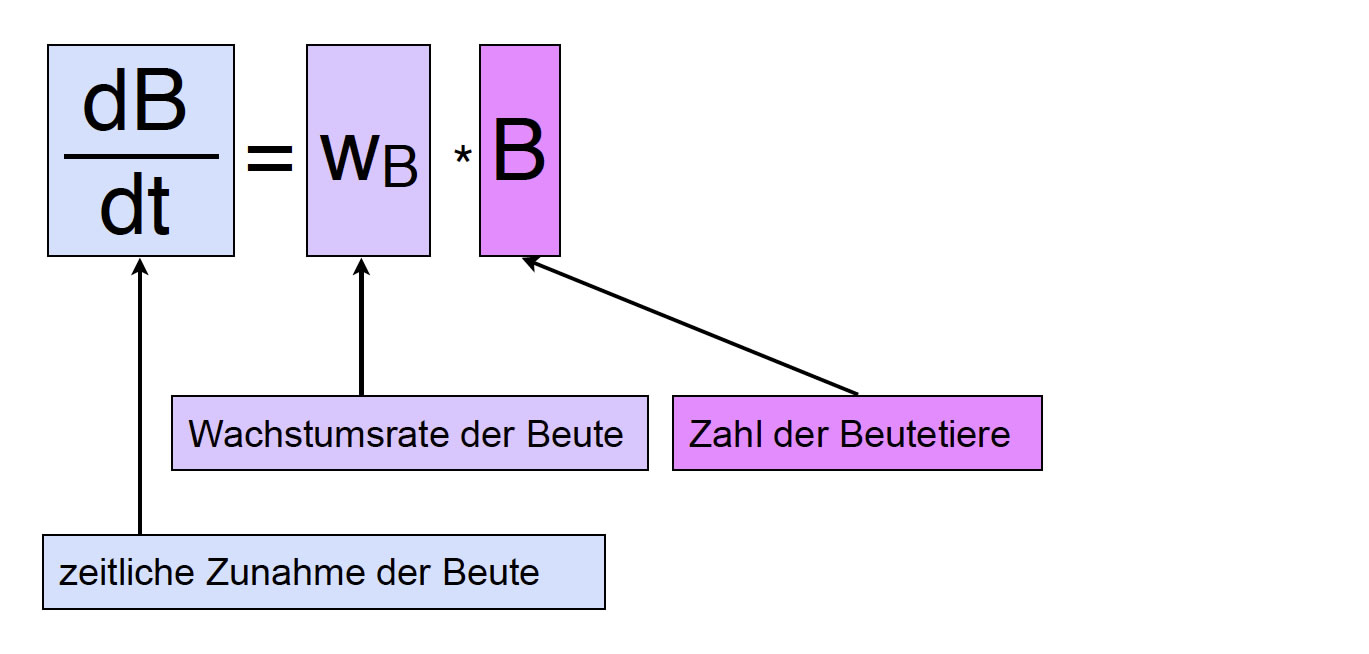
Differentialgleichung für das Wachstum der Beutepopulation
Die zeitliche Zunahme der Beute dB/dt hängt einmal von der Wachstumsrate wB der Beute ab und dann von der Anzahl B der bereits vorhandenen Beutetiere (oder -pflanzen). Simuliert man ein entsprechendes Wachstum mit einem Java-Programm oder mit einer Tabellenkalkulation, so erhält man stets eine exponentielle Wachstumskurve.
Populationswachstum der Beute in Anwesenheit von Räubern
Wie beeinflusst nun die Anwesenheit von Räubern dieses Populationswachstum der Beute. Rein anschaulich gesehen ist die Sache klar: Die Räuber fressen einen Teil der Beute, und daher wird das Populationswachstum der Beute gehemmt bzw. verlangsamt, es sei denn, die Beute reagiert mit einer erhöhten Wachstumsrate auf die Anwesenheit der Räuber. So legen manche Fischarten hunderttausende von Eiern, damit wenigsten ein paar von ihnen die Fressattacken der Räuber überleben. Aber auf dieser Seite wollen wir das Problem ja mathematisch angehen. Daher müssen wir die Differentialgleichung um einen Räuber-Faktor erweitern:
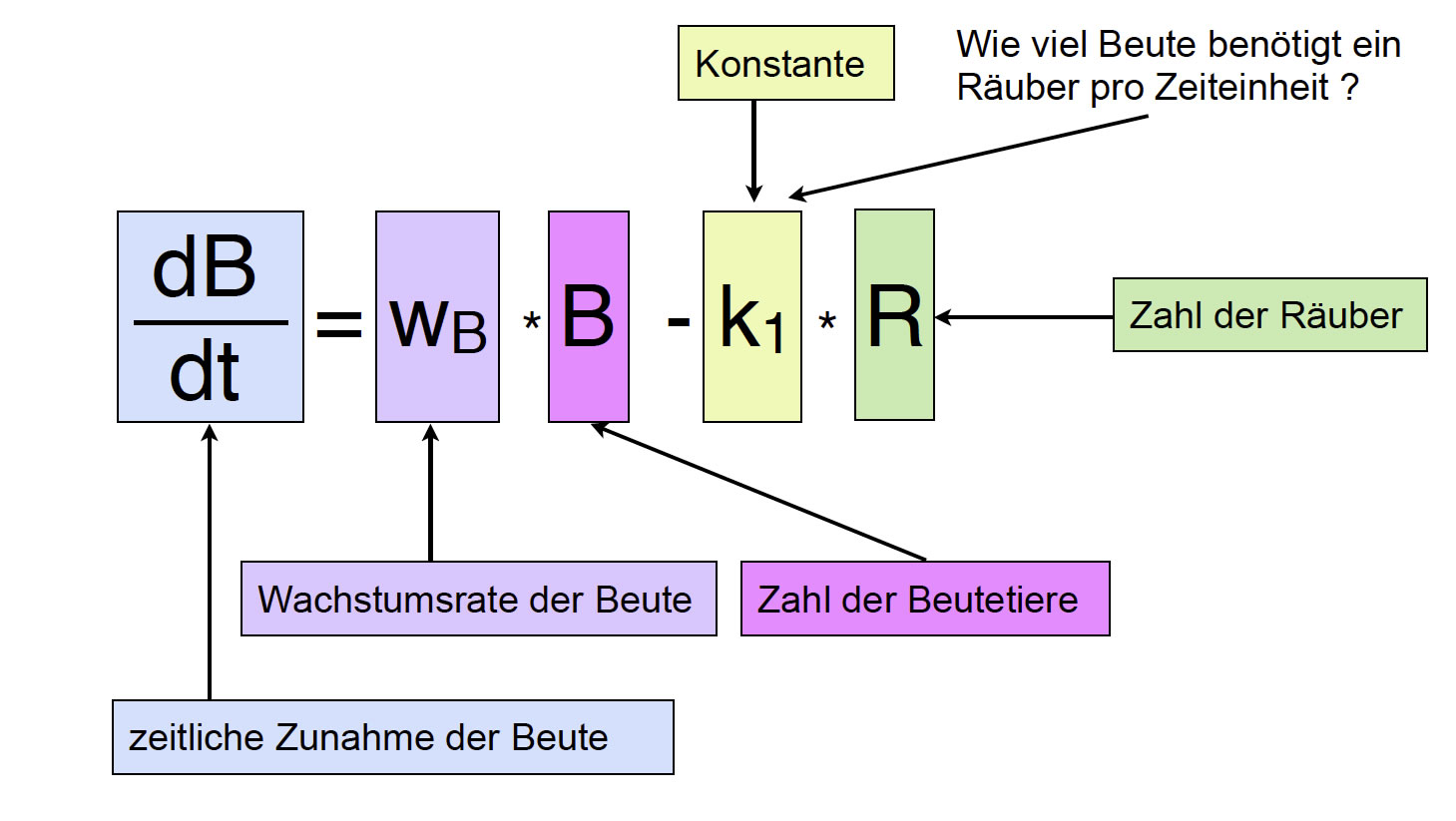
Erweiterte Differentialgleichung für das Wachstum der Beutepopulation
Die Konstante k1 beschreibt, wie viel Beute ein Räuber pro Zeiteinheit (Tag, Woche...) benötigt. R ist einfach die aktuelle Anzahl der Räuber.
Allerdings ist die Gleichung noch nicht ganz vollständig. Ein Räuber muss seine Beute ja erst mal erbeuten. Je weniger Beute vorhanden ist, desto schwieriger ist das für die Räuber. Die folgende Differentialgleichung berücksichtigt auch die Zahl der Beutetiere in dem Räuber-Term:
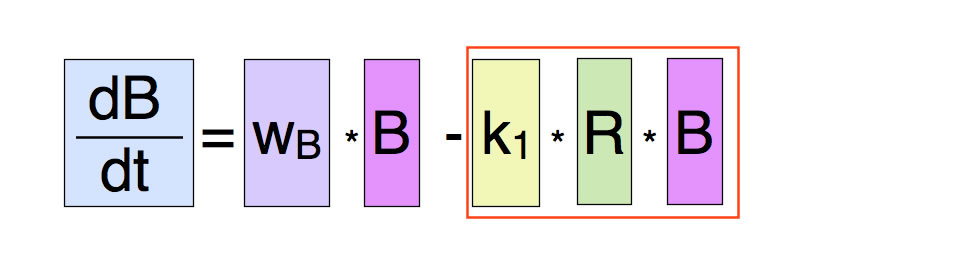
Nochmals erweiterte Differentialgleichung für das Wachstum der Beutepopulation
Auch die Räuber vermehren sich...
Dummerweise hat R keinen konstanten Wert, sondern die Anzahl der Räuber-Individuen unterliegt natürlichen Schwankungen. Wenn die Beute knapp ist, gibt es auch wenig Räuber. Ist viel Beute vorhanden, haben die Räuber genug zu fressen und vermehren sich entsprechend, so dass die Zahl der Räuber zunimmt.
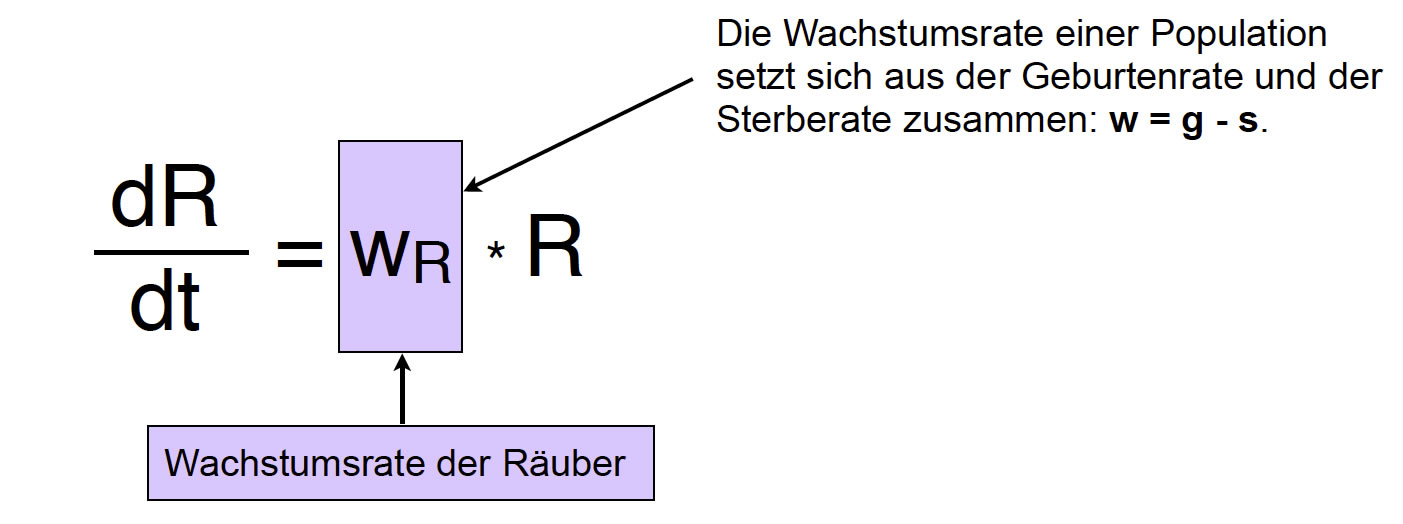
Differentialgleichung für das Wachstum der Räuberpopulation
Hier sehen wir die Differentialgleichung für das Wachstum einer Räuberpopulation. Die Wachstumsrate wR der Räuberpopulation ist aber keine Konstante, sondern setzt sich aus der nicht-konstanten Geburtenrate gR und der nicht-konstanten Sterberate sR zusammen: wR = gR - sR.
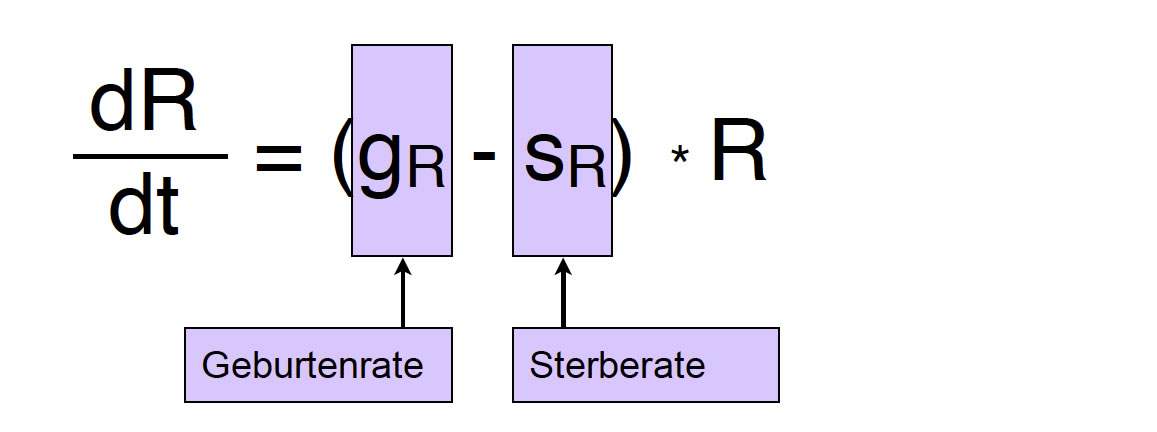
Differentialgleichung für das Wachstum der Räuberpopulation
Die Geburtenrate der Räuber ist nicht konstant, sondern hängt von der Zahl der Beutetiere ab. Je mehr Beute es zu fressen gibt, desto größer ist normalerweise auch die Geburtenrate der Räuber.
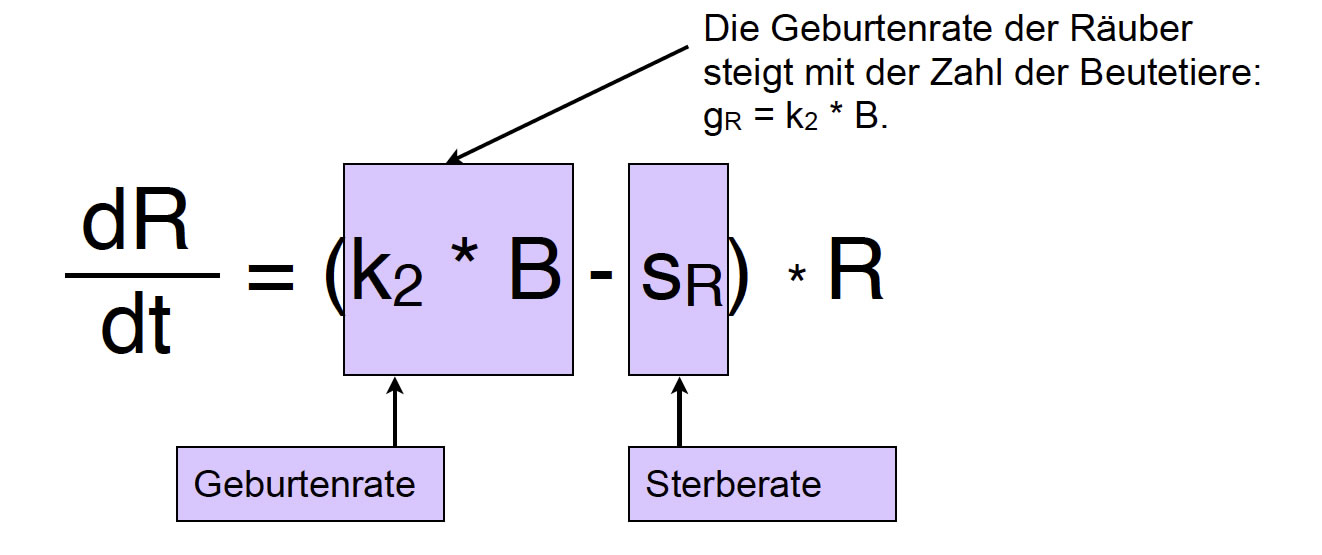
Erweiterte Differentialgleichung für das Wachstum der Räuberpopulation
Damit hätten wir beide Differentialgleichungen fertig. Die erste Gleichung beschreibt das Wachstum der Beute unter Berücksichtigung der Zahl der Räuber, und die zweite Gleichung beschreibt das Wachstum der Räuber unter Berücksichtigung der Zahl der Beute. Beide Differentialgleichungen hängen also zusammen, daher spricht man hier auch von gekoppelten Differentialgleichungen:
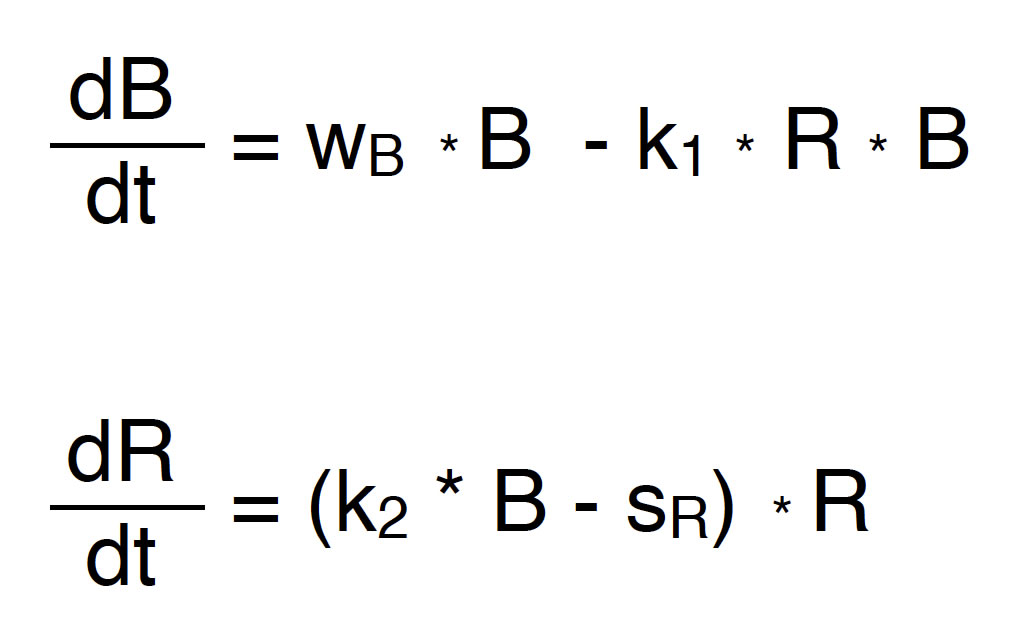
Die beiden gekoppelten Differentialgleichungen
Simulation am PC
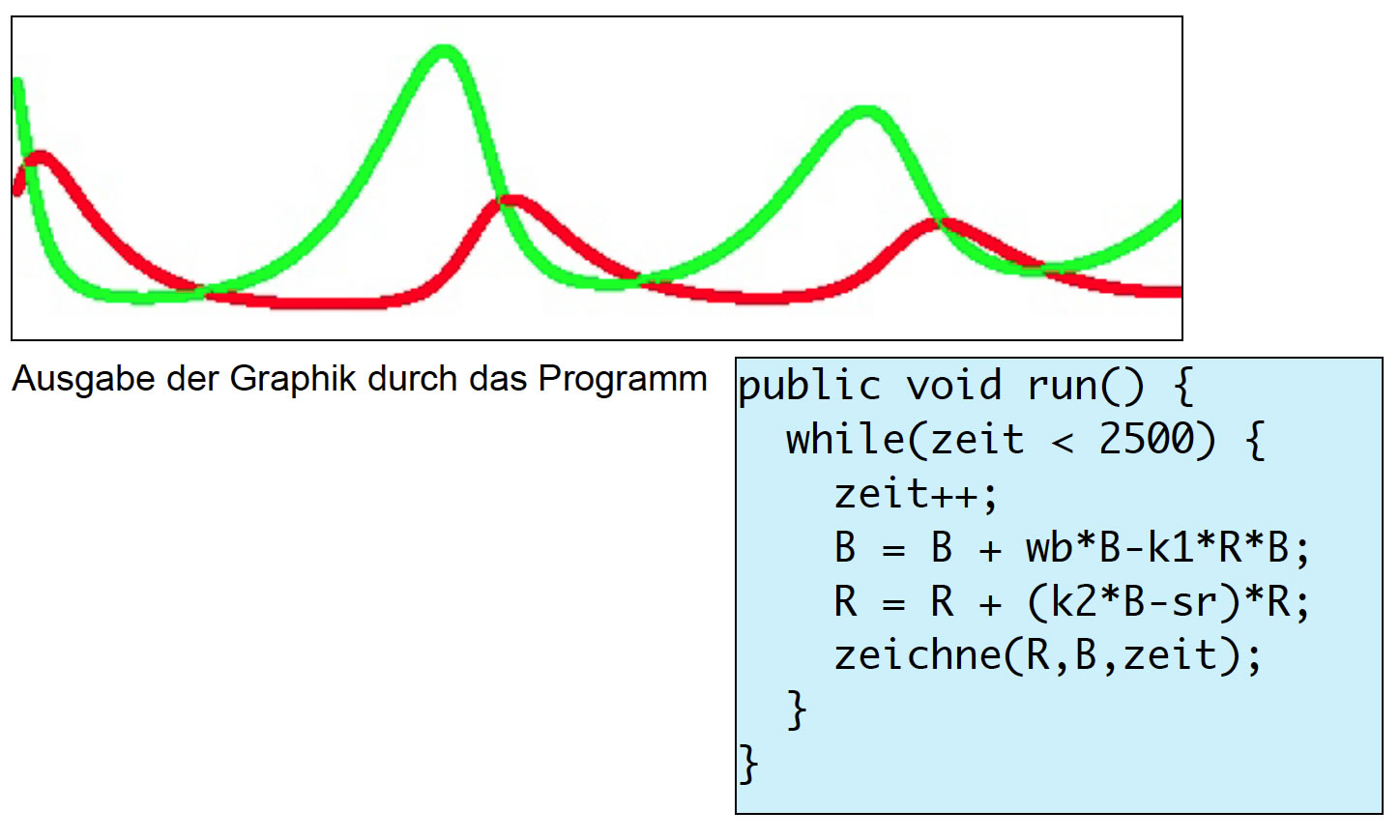
Eine Java-Methode zur Simulation des R/B-Systems und die graphische Ausgabe des Programms
Hier der Java-Quelltext der Methode, die das R/B-System simuliert:
public void run()
{
while (zeit < 2500)
{
zeit++;
B = B + wb*B - k1*R*B;
R = R + (k2*B-sr)*R;
zeichne(R,B,zeit);
}
}
Am Anfang hat die Variable zeit den Wert 0, bei jedem Schleifendurchgang wird zeit dann um 1 erhöht.
Die beiden nächsten Zeilen realisieren die beiden Differentialgleichungen, und der Befehl zeichne(R,B,zeit) ruft eine etwas komplexere Methode auf, welche die Zahl der Räuber und die Zahl der Beute in Abhängigkeit von der Zeit graphisch darstellt. Die Kurven, die dabei produziert werden, entsprechen in etwa den Kurven, die man in allen Biologie-Büchern findet, wenn man das Räuber-Beute-Kapitel aufschlägt.
Das größte Problem bei der Simulation war das Finden der passenden Konstanten wb, k1, k2 und sr. Hier musste ich sehr viel ausprobieren, bis am Ende einigermaßen gut aussehende Kurven produziert werden konnten.
Räuber-Beute-Spiel
In einer didaktischen Biologie-Zeitschrift wurde vor Jahren mal ein Räuber-Beute-Spiel veröffentlicht, das ich dann in ein Java-Programm umgesetzt habe.
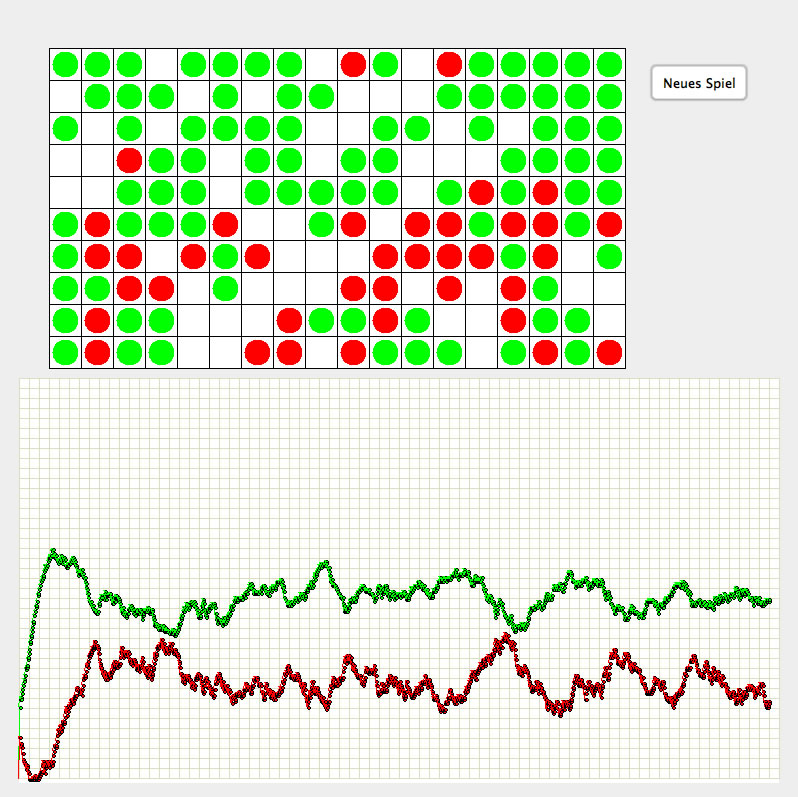
Schreenshot des Applets
Die grünen Kreise sollen Blättläuse, die roten Kreise Marienkäfer darstellen. Die Blattläuse vermehren sich nach bestimmten Regeln, und die Marienkäfer fressen die Blattläuse und vermehren sich auch nach bestimmten Regeln. Oben im Bild sieht man die letzte Besetzung des Spielfeldes mit Blattläusen und Marienkäfern, unten im Bild sind die Anzahlen der Tiere im Verlauf der Zeit graphisch dargestellt. Diese Kurven sehen anders aus als die "üblichen" Graphiken in den Schulbüchern, eher wie die "wirklichen" Räuber-Beute-Verhältnisse in der Natur.
Die Regeln dieses kleinen Spieles sind die folgenden:
Vermehrung der Blattläuse
Zunächst wird eine Position auf dem Spielfeld ausgewürfelt. Bei dem "richtigen" Brettspiel kann man dazu zwei Würfel verwenden, bei der Computersimulation werden einfach zwei Zufallszahlen ermittelt.
Regel 1: Trifft die neue Blattlaus auf ein noch leeres Feld, so besetzt die Blattlaus dieses Feld - es wird ein grüner Kreis gezeichnet.
Regel 2: Trifft die neue Blattlaus auf ein Feld, das bereits von einer Blattlaus besetzt ist, so besetzt die neue Blattlaus eines der angrenzenden freien Felder. Ist kein angrenzendes Feld frei, so passiert nichts.
Regel 3: Trifft die neue Blattlaus auf ein Feld, das von einem Marienkäfer besetzt ist, so passiert nichts.
Vermehrung der Marienkäfer
Auch hier wird zunächst eine Position auf dem Spielfeld ausgewürfelt.
Regel 1: Trifft der neue Marienkäfer auf ein leeres Feld, so passiert nichts.
Regel 2: Trifft der neue Marienkäfer auf ein Feld, das bereits von einem Marienkäfer besetzt ist, passiert nichts.
Regel 3: Trifft der neue Marienkäfer auf ein von einer Blattlaus besetztes Feld, so wird die Blattlaus gefressen und der Marienkäfer wird auf das Feld gesetzt. Die Blattlauspopulation wird so um 1 vermindert, die Marienkäferpopulation um 1 erhöht.
Quelltexte
Wer sich für die Quelltexte dieser Simulation interessiert, kann sie sich gerne als Textdatei herunterladen. Ich übernehme allerdings keine Gewähr für korrektes Funktionieren des Applets.
Wator
WATOR ist eine Räuber-Beute-Simulation, die ebenfalls in einer "Rechteck-Welt" stattfindet. Der Quelltext dieser schönen Simulation kann auf dieser Webseite heruntergeladen werden. Es handelt sich um ein aufwendiges Java-Applet mit vielen Klassen, die aber alle in einer Datei untergebracht sind. Mit der Entwicklungsumgebung BlueJ kann diese Datei mühelos kompiliert und ausgeführt werden.