Lernziele
Wenn Sie diese Seite durchgearbeitet haben, sollten Sie
- wissen, was exponentielles Wachstum überhaupt ist,
- die mathematischen Grundlagen zum exponentiellen Wachstum beherrschen,
- die Begriffe Wachstumsrate, Geburtenrate und Sterberate kennen und in Beziehung zum exponentiellen Wachstum setzen können,
- ein exponentielles Wachstum mit Hilfe einer gängigen Tabellenkalkulation simulieren können.
Exponentielles Wachstum bei Bakterien
"Abhängig vom Organismus und den Kulturbedingungen, kann die Generationszeit von Einzellern ca. 15 Minuten (thermophile Bakterien), mehrere Stunden (z.B. nitrifizierende Bakterien) oder mehrere Tage betragen".
Quelle: Spektrum Lexikon der Biologie, Stichwort "mikrobielles Wachstum"
Bakterien der Art Escherichia coli können sich unter optimalen Bedingungen alle 20 Minuten teilen. Aus einem Individuum werden nach 20 Minuten zwei, nach 40 Minuten vier, nach einer Stunde acht, und so weiter. Schauen wir uns mal eine graphische Darstellung des Populationswachstums von Escherichia coli an:
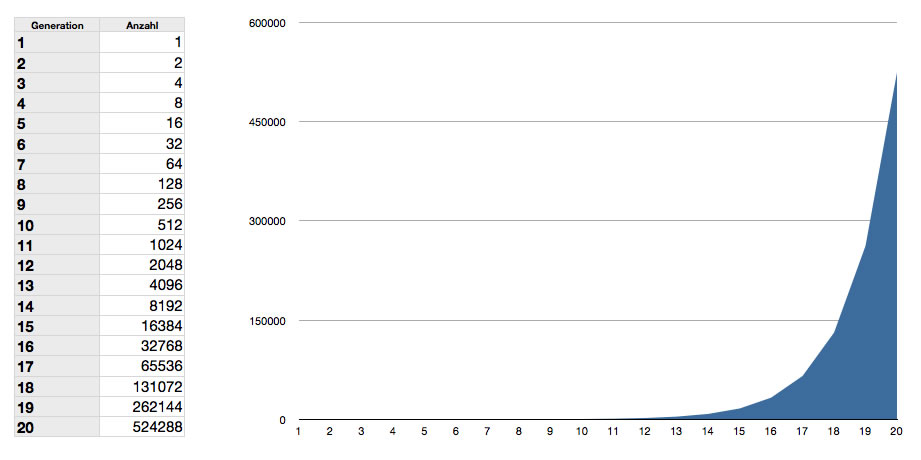
Berechnung des Populationswachstums von E. coli für 20 Generationen
Ich habe hier mit einer Tabellenkalkulation die Entwicklung einer E. coli-Kolonie über einen Zeitraum von zwanzig Generationen (also gut sechs Stunden) berechnen und graphisch darstellen lassen. Nach gut sechs Stunden gibt es bereits eine halbe Million Zellen, 20 Minuten später ca. 1 Million Zellen.
Hier sehen wir auch gleich etwas ganz Typisches für das exponentielle Wachstum: Am Anfang sieht das Wachstum total harmlos aus, man könnte fast von einem Nullwachstum sprechen - was natürlich auch an dem hier verwendeten Maßstab liegt. Erst nach ca. 14 oder 15 Generationen sieht man ein deutliches Wachstum, das sich dann immer mehr steigert.
Exponentielles Wachstum in der Natur
Nicht nur bei Bakterien hat man exponentielles Wachstum beobachtet, auch bei vielen höheren Organismen (Pflanzen, Tiere, Menschen) kennt man Phasen exponentiellen Wachstums. Das Populationswachstum der Menschheit ist sogar hyperexponentiell, also noch stärker als einfaches exponentielles Wachstum.
Wachstum der Menschheit
Im Jahre 1804 lebten eine Milliarde Menschen auf der Erde, im Jahre 1927 verdoppelte sich die Zahl auf zwei Milliarden. Der Verdopplungszeitraum belief sich auf 123 Jahre.
Im Jahre 1974 gab es bereits vier Milliarden Menschen auf der Erde, der Verdopplungszeitraum betrug jetzt nur noch 47 Jahre.
Zur Zeit (17.6.2018) gibt es 7.480.144.000 Menschen, nächstes Jahr (2019) wird die Zahl vermutlich auf 8 Milliarden gewachsen sein. Der Verdopplungszeitraum beträgt jetzt also 44 Jahre, das ist nochmals eine Beschleunigung des Wachstums. Aber scheinbar nähert sich das Wachstum der Menschheit einem exponentiellen Wachstum an, also einem Wachstum mit konstanter Verdopplungszeit. Das ist ja schon mal beruhigend (Achtung: Sarkasmus!).
Das stärkste Bevölkerungswachstum gibt es in den Entwicklungsländern, während in den meisten Industrieländern das Bevölkerungswachstum stagniert oder sogar negativ verläuft.
Auf der Seite www.census.gov/popclock können Sie der Menschheit beim Wachsen regelrecht zusehen.
Mathematik des exponentiellen Wachstums
Die mathematische Darstellung exponentiellen Wachstums ist recht einfach. Die konstante Verdopplungszeit ist abhängig von der Wachstumsrate w der Population. Die Wachstumsrate wiederum setzt sich aus zwei Komponenten zusammen: Der Geburtenrate g und der Sterberate s. Es gilt: w = g - s. Wenn mehr Individuen geboren werden als welche sterben, ist die Wachstumsrate positiv. Sterben mehr Individuen in einem Zeitraum, als geboren werden, ist die Wachstumsrate negativ, also kleiner als 0. Halten sich Geburtenrate und Sterberate die Waage, hat die Wachstumsrate den Wert 0, man spricht dann von einer Stagnation der Population oder von einen Nullwachstum.
Für die Simulation exponentiellen Wachstums mit einer Tabellenkalkulation benötigt man eine Differentialgleichung. Die Differentialgleichung gibt an, wie stark die Population innerhalb eines bestimmten Zeitraums zunimmt (oder abnimmt).
$\frac{dN}{dt} = k N$
Mit $dN$ ist die Zunahme der Populationsgröße gemeint, mit $dt$ der Zeitraum, in dem die Zunahme stattfindet. Die Konstante $k$ bestimmt, wie stark $\frac{dN}{dt}$ von der aktuellen Populationsgröße $N$ abhängt.
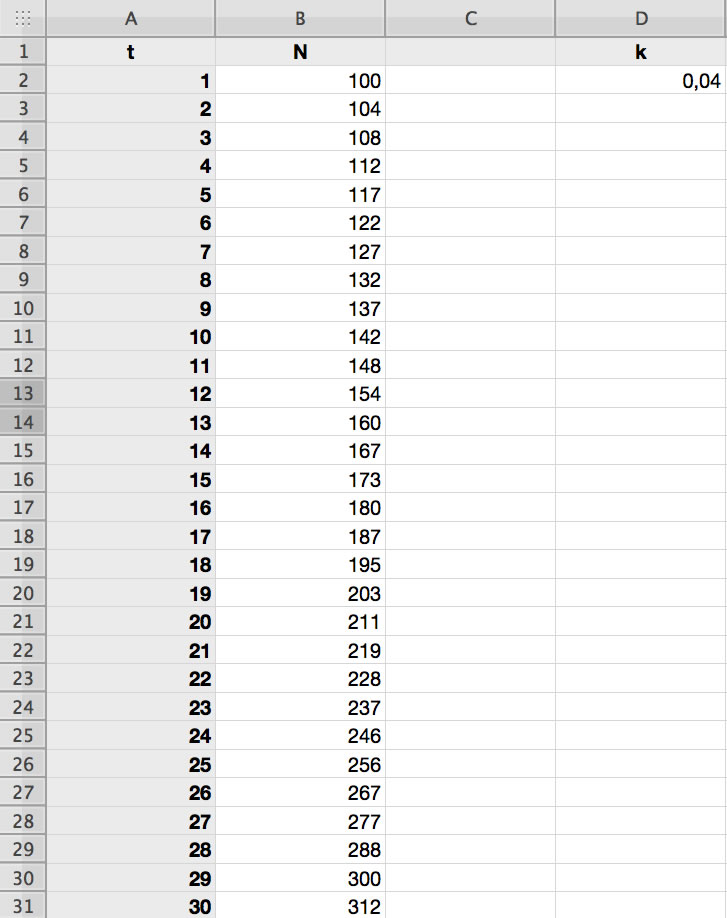
Simulation exponentiellen Wachstums durch eine Tabellenkalkulation (Apple Numbers)
Methodentraining Tabellenkalkulation I
In die erste Spalte der Tabellenkalkulation tragen wir die Generationen ein, also 1, 2, 3, ... 30. Dazu kann man bereits eine einfache Formel verwenden. Der Wert der Zelle A3 berechnet sich beispielsweise aus dem Wert der Zelle A2, erhöht um 1. In die Zelle A3 tragen wir also folgende Formel ein:
=A2+1
Diese Formel kopieren wir dann in alle unterhalb von A3 stehenden Zellen A4, A5, ... A31.
In die Zelle B2 tragen wir die Ausgangsgröße der Population ein, hier also 100.
In die Zelle D2 tragen wir den Werte der Konstante k der Differentialgleichung ein, also beispielsweise 0,04.
Dann schreiben wir die folgende Formel in die Zelle B3:
= B2 + D$2*B2
Diese Formel kopieren wir wieder in alle Zellen unterhalb von B3. Wahrscheinlich werden die Zahlen jetzt mit vielen Nachkommastellen dargestellt, was nicht schön aussieht. Wir formatieren die Spalte B daher so, dass keine Nachkommastellen mehr angezeigt werden. Wie das geht, hängt ganz von der verwendeten Tabellenkalkulation ab.
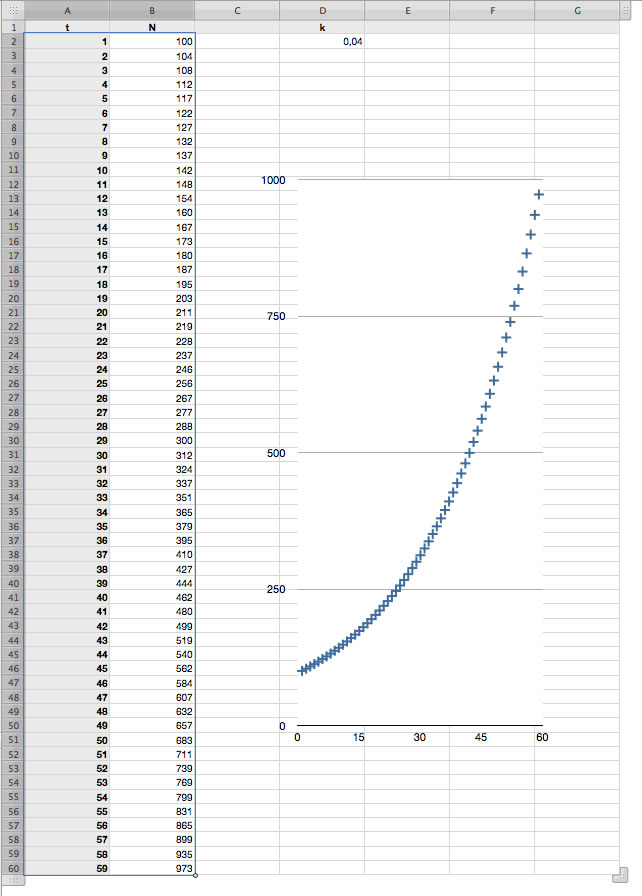
Erstellung eines Diagramms
Mit einer Tabellenkalkulation kann man die Zahlenkolonnen auch sehr schön graphisch darstellen. Dazu markiert man mit der Maus die beiden Spalten A und B und wählt dann eine entsprechende Darstellungsform aus. In der Abbildung 2 wurde die Darstellungsart "x/y-Diagramm" gewählt. Diese Darstellungsart erzeugt einen richtigen mathematischen Funktionsgraphen, der die Werte der einen Spalte (hier B) in Abhängigkeit von den Werten der anderen Spalte (hier A) darstellt.
Die nach Excel konvertierte Numbers-Tabelle können Sie sich übrigens hier herunter laden. Auf Schönheit wurde hier kein Wert gelegt, das können Sie dann ja machen.
Aufgabe 1
Wir wollen einmal recherchieren, wie groß ein Bakterium der Art Escherichia coli ist. Das Spektrum Lexikon der Biologie liefert uns konkrete Zahlen: "E. coli-Bakterien sind gerade Stäbchen, 1,1–1,5 × 2,0–6,0 μm (lebend)". Für diese Aufgabe gehen wir einmal von einer durchschnittlichen Länge von 4 μm und einer durchschnittlichen Breite von 1,3 μm aus. Die Höhe eines solchen Bakteriums wollen wir dann auch mit 1,3 μm ansetzen.
Um die Aufgabe lösen zu können, müssen Sie außerdem wissen, was man überhaupt unter 1 μm versteht. 1 μm oder 1 Mikrometer ist der tausendste Teil eines Millimeters und der millionste Teil eines Meters.
Aufgabenstellung
Escherichia coli verdoppelt sich unter Idealbedingungen alle 20 Minuten. Angenommen, eines dieser Bakterien könnte sich einen Tag lang völlig ungehindert durch Wände und andere Hindernisse unter Idealbedingungen vermehren, wie dick wäre dann die Bakterienschicht, die das Festland der Erde bedecken würde? Die Landfläche der Erde beträgt laut Wikipedia etwa 149,4 Millionen km²
Aufgabe 2
Laut Süddeutscher Zeitung ("Die Wucht der großen Zahl") hatten sich am 10. März 2020 1.218 Menschen in Deutschland mit dem Corona-Virus infiziert. Am 24. März waren es bereits 4.872 Infizierte, am 7. April 19.488 Infizierte und am 21. April 77.952 Infizierte.
Aufgabenstellung
Analysieren Sie diese Zahlen und beurteilen Sie dann, ob es sich hier um ein exponentielles Wachstum handelt.
Alternativen zum exponentiellen Wachstum sind das hyper-exponentielle Wachstum und das hypo-exponentielle Wachstum. Beim hyper-exponentiellen Wachstum ("hyper" = über) verkürzt sich der Verdopplungszeitraum ständig, während beim hypo-exponentiellen Wachstum ("hypo" = unter) die Verdopplungszeiträume immer länger werden. Beim exponentiellen Wachstum sind die Verdopplungszeiträume konstant.
Aufgabe 3
In einem Biologiebuch steht ein schönes Beispiel für reales exponentielles Wachstum: Zunahme der Schreikranich-Population in Texas. Hier die Zahlen als Tabelle:
| Jahr | N |
| 1940 | 18 |
| 1945 | 17 |
| 1950 | 30 |
| 1955 | 20 |
| 1960 | 31 |
| 1965 | 42 |
| 1970 | 55 |
| 1975 | 48 |
| 1980 | 75 |
| 1985 | 90 |
| 1990 | 145 |
| 1995 | 155 |
| 2000 | 174 |
Aufgabenstellung
Analysieren Sie diese Zahlen und beurteilen Sie dann, ob es sich hier um ein exponentielles Wachstum handelt.
