12.2 Binäre Suche

1. Ein Ratespiel

Bereits mit einfachen Java-Kenntnissen (Fallunterscheidungen, Schleifen) kann man ein kleines Zahlenratespiel programmieren.

Das Programm erzeugt mit einem Zufallsgenerator eine ganze Zahl z zwischen 1 und 100. Der Benutzer versucht, diese Zahl durch Eingabe einer Ratezahl r zu erraten.

Ist die Ratezahl größer als die gesuchte Zahl, gibt das Programm "Zahl zu groß" aus. Ist sie kleiner, erscheint die Meldung "Zahl zu klein". Stimmen beide Zahlen überein, meldet das Programm den Erfolg und zeigt die Anzahl der benötigten Versuche an.

Fallbeispiel

Gesucht wird die Zahl 16. Ein systematisches Vorgehen könnte folgendermaßen aussehen:

Wie könnte man dieses Vorgehen beschreiben?

Man beginnt mit einer Zahl ungefähr in der Mitte des möglichen Zahlenbereichs. Ist die Ratezahl zu groß, weiß man, dass die gesuchte Zahl kleiner sein muss. Die obere Hälfte des bisherigen Bereichs kann daher ausgeschlossen werden. Ist die Ratezahl dagegen zu klein, kann man die untere Hälfte ausschließen.

Nun betrachtet man nur noch den verbleibenden Zahlenbereich und wählt wieder eine Zahl ungefähr in dessen Mitte. Dieses Vorgehen wird so lange wiederholt, bis die gesuchte Zahl gefunden wurde.

Auf diese Weise wird der mögliche Zahlenbereich bei jedem erfolglosen Versuch ungefähr halbiert. Statt alle Zahlen von 1 bis 100 nacheinander auszuprobieren, benötigt man daher nur wenige Versuche.

Dieses Prinzip bildet die Grundlage der binären Suche, die wir im nächsten Abschnitt genauer untersuchen werden.

Lösung

Stellen wir dazu folgende Zahlenreihe auf:

1000 ⟹ 500 ⟹ 250 ⟹ 125 ⟹ 62 ⟹ 31 ⟹ 16 ⟹ 8 ⟹ 4 ⟹ 2 ⟹ 1

Bei der binären Suche wird die Anzahl der zu durchsuchenden Elemente mit jedem Suchschritt halbiert - das soll die obige Zahlenreihe verdeutlichen. Nach spätestens 10 Suchschritten (durch die Pfeile symbolisiert) ist die gesuchte Zahl eindeutig bestimmt.

2. Der Algorithmus der binären Suche

Die folgende Abbildung zeigt ein Flussdiagramm der binären Suche in einem aufsteigend sortiertem Array:

Flussdiagramm der binären Suche
Autor: Ulrich Helmich 2/2026, Lizenz: Public domain

Beschreibung des Flussdiagramms

Wir beginnen links oben bei "Start". Zunächst wird der Suchwert eingegeben. Anschließend werden zwei lokale Variablen festgelegt:

links = 0

rechts = array.length - 1

Diese beiden Variablen begrenzen den Bereich des Arrays, in dem gesucht werden soll. Bei einem Array mit 100 Elementen hat links zunächst den Wert 0 und rechts den Wert 99. Der gesamte Arraybereich wird also berücksichtigt.

1. Ist der Suchbereich noch gültig?

Die erste Fallunterscheidung überprüft die Bedingung links <= rechts. Solange diese Bedingung erfüllt ist (true), enthält der Suchbereich noch mindestens ein Element. Ist dagegen links > rechts, gibt es keine Elemente mehr, die durchsucht werden können. Die Suche wird dann mit "nicht gefunden" beendet.

2. Die Mitte des Suchbereichs bestimmen

Ist der Suchbereich noch gültig, wird der Index des mittleren Elements berechnet:

mitte = (links + rechts) / 2

Bei einem Array mit 100 Elementen ergibt sich zunächst (0 + 99) / 2 = 49,5. Da beide Variablen vom Typ int sind, wird bei der Division der Nachkommateil abgeschnitten. Die Variable mitte erhält also den Wert 49.

3. Ist das mittlere Element der gesuchte Wert?

Nun wird überprüft, ob das mittlere Arrayelement mit dem Suchwert übereinstimmt:

array[mitte] == suchwert

Ist diese Bedingung erfüllt (true), wurde die gesuchte Zahl gefunden. Die Suche ist beendet, und der Index mitte wird ausgegeben.

4. In welcher Hälfte müssen wir weitersuchen?

Wurde die Zahl nicht gefunden, wird das mittlere Arrayelement mit dem Suchwert verglichen:

array[mitte] > suchwert

Ist das mittlere Element größer als der Suchwert, kann sich die gesuchte Zahl nur in der linken Hälfte befinden. Deshalb wird die rechte Grenze verschoben:

rechts = mitte - 1

Ist das mittlere Element dagegen kleiner als der Suchwert, kann sich die gesuchte Zahl nur in der rechten Hälfte befinden. Deshalb wird die linke Grenze verschoben:

links = mitte + 1

Das mittlere Element selbst muss nicht mehr berücksichtigt werden, denn wir wissen bereits, dass es nicht der gesuchte Wert ist.

5. Der nächste Schleifendurchgang

Nachdem eine der beiden Grenzen verändert wurde, beginnt der nächste Schleifendurchgang. Zunächst wird erneut überprüft, ob links <= rechts gilt. Ist dies der Fall, wird die Mitte des jetzt kleineren Suchbereichs neu berechnet und die Suche fortgesetzt.

Dieser Ablauf lässt sich in Java sehr gut mit einer while-Schleife umsetzen.

Die Suche endet, sobald eine der folgenden Bedingungen erfüllt ist:

• Erfolgreiche Suche: Der Suchwert wurde gefunden (array[mitte] == suchwert).
• Erfolglose Suche: Der Suchbereich ist leer geworden (links > rechts).

Das Besondere an der binären Suche ist, dass bei jedem erfolglosen Vergleich ungefähr die Hälfte des bisherigen Suchbereichs ausgeschlossen wird. Bei einem Array mit 100 Elementen sind deshalb höchstens sieben Vergleiche mit Arrayelementen notwendig, um die gesuchte Zahl zu finden oder festzustellen, dass sie nicht vorhanden ist.

3. Implementierung einer binären Suche

Betrachten wir nun eine einfache Implementierung der binären Suche in einem aufsteigend sortierten Array aus positiven int-Zahlen. Das Array liegt als Instanzvariable zahlen vor, muss der Suchmethode also nicht als Parameter übergeben werden. Die Methode gibt den Index der gefundenen Zahl zurück oder - falls die Zahl nicht im Array enthalten ist - den Wert -1.

public int binaereSuche(int suchzahl)
{
    int links = 0;
    int rechts = zahlen.length - 1;

    while (links <= rechts)
    {
        int mitte = (links + rechts) / 2;

        if (zahlen[mitte] == suchzahl)
            return mitte;

        if (zahlen[mitte] > suchzahl)
            rechts = mitte - 1;
        else
            links = mitte + 1;
    }

    return -1;
}

Erläuterung

Die Variablen links und rechts begrenzen den Bereich des Arrays, in dem sich die gesuchte Zahl noch befinden kann.

In jedem Durchgang der while-Schleife wird

1. Mit mitte der mittlere Index des aktuellen Suchbereichs berechnet.
2. Überprüft, ob die Zahl an dieser Position der gesuchten Zahl entspricht. Falls ja, wird der Index zurückgegeben.
3. Falls die Zahl zu groß ist, wird die rechte Grenze nach links verschoben.
4. Falls die Zahl zu klein ist, wird die linke Grenze nach rechts verschoben.

Die Schleife läuft so lange, wie links <= rechts gilt. Ist der Suchbereich leer (links > rechts), endet die Schleife und die Methode liefert -1.

3. Einschätzung der Suchzeit

Wir suchen die Zahl 16 in einem sortierten Array aus 32 int-Zahlen im Bereich zwischen 1 und 92.

Schritt 1

links = 0, rechts = 31

mitte = (0 + 31) / 2 = 15.5 = 15

Die Zahl an Index 15 (mitte) hat den Wert 32. Die Suchzahl 16 muss sich also in der linken Hälfte befinden, und dort suchen wir weiter.

Schritt 2

links = 0, rechts = mitte - 1 = 14

mitte = (0 + 14) / 2 = 7

Die Zahl 14 in der Mitte der linken Hälfte ist kleiner als die Suchzahl, also machen wir in der rechten Hälfte dieses Bereichs weiter.

Schritt 3

Die Zahl 21 in der Mitte dieses Abschnitts ist größer als die Suchzahl, also machen wir in der linken Hälfte dieses Bereichs weiter.

Schritt 4

Der Wert des mittleren Elements entspricht der Suchzahl, also können wir die Suche jetzt erfolgreich abschließen.

Einschätzung der Suchzeit

Bei der binären Suche wird der Suchbereich nach jedem erfolglosen Vergleich ungefähr halbiert. In unserem Beispiel sind vier solcher Vergleiche bzw. Suchschritt notwendig.

Bei der sequentiellen Suche in einem unsortierten Array würde man im Schnitt N/2 = 32/2 = 16 Vergleiche benötigen, um eine Zahl zu finden.

Würde man die 16 in dem sortierten Array sequentiell suchen, müssten wir 10 Vergleiche durchführen.

4. Quantitative Betrachtungen

Bei der binären Suche wird die Anzahl der zu durchsuchenden Elemente bei jedem Suchschritt um 50% reduziert.

Wenn wir ein Array mit 1024 Elementen haben, besteht der erste Schritt in der Bestimmung der Mitte des Arrays und der Entscheidung, ob das Element bereits gefunden wurde bzw. in welcher Hälfte des Arrays man weitersuchen muss.

Der zweite Schritt arbeitet genau so wie der erste, nur die Anzahl der zu durchsuchenden Elemente hat sich auf 512 reduziert (streng genommen auf 511, weil ja nicht nur die eine Hälfte des Arrays wegfällt, sondern auch die Mitte des ursprünglichen Arrays).

Im dritten Schritt müssen nur noch 256 Elemente durchsucht werden, im vierten Schritt 128 und so weiter.

Die Zahl der Suchschritte entspricht also ungefähr dem Zweierlogarithmus der Anzahl der zu durchsuchenden Elemente. Für 1024 Elemente würde man also maximal 10 Suchschritte brauchen, für 10.000 Elemente maximal 14 Schritte.

Lösungsvorschlag auf den Seiten für Lehrer(innen) / Nähere Infos dazu

Bei der linearen Suche hatten wir den Zeitaufwand O(N) = N charakterisiert. Bei der binären Suche ist der Zeitaufwand nur noch O(N) = log₂ N, also erheblich geringer.

5. Nachteil der binären Suche

Auch die binäre Suche ist nicht die schnellste Suche, allerdings ist sie deutlich schneller als die lineare Suche.

Kommen wir noch einmal auf unser Bücher-Beispiel zurück. Wenn Sie nach dem russischen Science Fiction-Autor Isaac Asimov suchen, werden Sie im echten Leben mit Sicherheit nicht in der Mitte des Regals mit der Suche beginnen, sondern am Anfang des Regals, wo die Autoren stehen sollten, deren Nachname mit 'A' beginnt. Die binäre Suche kann also noch erheblich optimiert werden. Damit werden wir uns aber erst im übernächsten Kapitel beschäftigen, der Interpolationssuche und der Indexsuche.

6. Übungen zur binären Suche

Aufgabe 12.2-4

Eine Schülerin hat ein Flussdiagramm zur binären Suche gezeichnet:

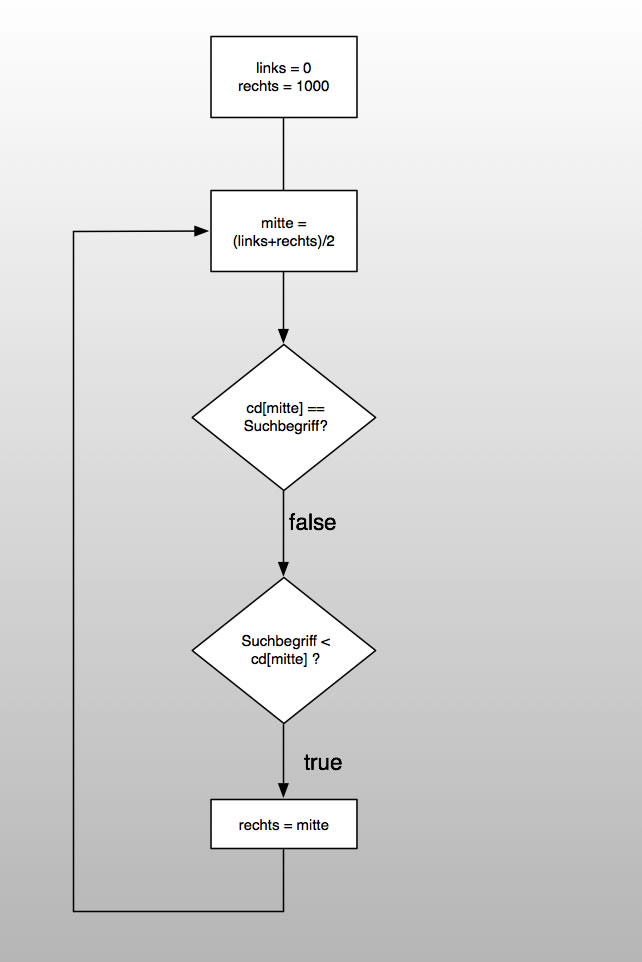
Dieser Entwurf enthält leider noch einige Fehler. Suchen und korrigieren Sie die Fehler, indem Sie ein sauberes und fehlerfreies Flussdiagramm zeichnen, dass die binäre Suche darstellt.

Lösungsvorschlag auf den Seiten für Lehrer(innen) / Nähere Infos dazu

public int suchzeitBinaer(int suchzahl)

7. Zur binären Suche

Die binäre Suche ist ein Sucherverfahren für sortierte Daten, das wesentlich schneller ist als die sequentielle Suche. Dennoch verwendet man in der Informatik meistens andere Suchverfahren als die binäre Suche.

So richtig optimal ist die binäre Suche eigentlich nicht. Das können Sie sich selbst ganz einfach klar machen. Wir kommen dazu noch einmal auf das Aufmacherbild am Anfang dieser Seite zurück: Sie stehen vor einem Bücherregal, die Bücher sind alphabetisch nach Name des Autors sortiert.

Wenn Sie jetzt ein Buch von Karl Zuselmeier suchen, werden Sie doch bestimmt nicht genau in der Mitte des Regals mit der Suche anfangen, sondern am rechten Ende, wo Sie die Bücher vermuten, deren Autorennamen mit X, Y oder Z beginnen.

Und wenn Sie ein Buch von Jürgen Alhorn suchen, werden Sie bestimmt ganz links im Regel anfangen, wo die A- und B-Autoren stehen.

Es gibt mehrere Verfahren, solche Suchen zu realisieren. Drei davon werden wir auf den folgenden Seiten kennenlernen, nämlich die Sprungsuche, die Indexsuche und die Interpolationssuche. Bevor wir dazu kommen, möchte ich aber noch einen sehr wichtigen Punkt ansprechen:

Was sind eigentlich "suchfreundlich organisierte" Daten ?

Auf der Eingangsseite zu den Suchalgorithmen hatten wir vier verschiedene Situationen unterschieden:

1. Die Daten sind unsortiert.
2. Die Daten sind zwar sortiert, das Suchkriterium entspricht aber nicht dem Sortierkriterium.
3. Die Daten sind sortiert, und das Suchkriterium entspricht dem Sortierkriterium.
4. Die Daten sind suchfreundlich sortiert und das Suchkriterium entspricht dem Sortierkriterium.

Was versteht man nun unter suchfreundlich organisierten Daten?

Betrachten wir dazu noch einem ein Array aus aufsteigend sortierten int-Zahlen:

Bei der binären Suche, die wir ja auf dieser Seite kennengelernt haben, muss man zunächst die mittlere Zahl finden und dann schauen, ob die Suchzahl in dem linken oder in dem rechten Teilarray vorkommt. Mit diesem Array verfährt man dann genau so.

Die Elemente dieser Datenstruktur sind zwar übersichtlich und sortiert angeordnet, aber nicht unbedingt suchfreundlich. Betrachten wir jetzt einmal eine tatsächlich suchfreundlich angeordnete Struktur der selben Daten.

Ein binärer Suchbaum
Autor: Ulrich Helmich, erstellt von Mistral Vibe nach den Vorgaben des Autors.

Hier sehen wir einen sogenannten binären Suchbaum. Die Zahlen sind hier völlig anderes organisiert als in einer linearen Liste bzw. einem Array.

Wir wollen in diesem Baum nach der 16 suchen. Dazu beginnen wir an der sogenannten Wurzel des Baumes, die den Wert 32 besitzt. Da die 16 kleiner ist als der Wert der Wurzel, wird im linken Teilbaum weitergesucht.

Dessen Wurzel hat den Wert 14. Die 16 ist größer als 14, also wird im rechten Teilbaum der 14 weitergesucht. Die Wurzel dieses Teilbaums ist 21, das heißt, wir müssen im linken Teilbaum der 21 weitersuchen.

Die Wurzel des linken Teilbaums ist 16, und damit haben wir die gesuchte Zahl schon gefunden - nach vier Vergleichen.

Vergleich Array / Suchbaum

Das sortierte Array

Die binäre Suche funktioniert hier problemlos, weil das Array bereits sortiert ist. Die Ordnung steckt hier aber nur in den Werten, nicht in der Datenstruktur. Der binäre Suchalgorithmus muss bei jedem Durchgang eine ganze Reihe von Berechnungen durchführen - Ermittlung der Mitte, Neubestimmung der Variablen links oder rechts.

Wenn - und das kommt bei echten Datensammlungen ja regelmäßig vor - neue Element in das Array eingefügt werden sollen, wird es kompliziert. Damit die Ordnungsstruktur aufrecht erhalten bleibt, müssen neue Elemente sofort an der richtigen Position eingefügt werden. Soll in das Array

beispielsweise die 8 eingefügt werden, so müssen alle Elemente ab dem Index 5 (Wert = 9) um eine Position nach rechts verschoben werden. Das ist ein enormer Aufwand für ein so kleines Array. Bei einem richtig großen Array oder einer ArrayList mit über 10.000 Elementen wäre dieser Aufwand riesig.

Das Gleiche gilt für das Löschen von Elementen. Wenn zum Beispiel die 9 gelöscht werden soll, müssen alle Elemente rechts der 9 um je eine Position nach links rücken - wieder ein großer Aufwand.

Und dieser ganze Aufwand ist erforderlich, damit das Array sortiert bleibt und die Suchalgorithmen weiterhin fehlerfrei funktionieren.

Der binäre Suchbaum

Bei einem Suchbaum steckt die Sortierung bereits in der Datenstruktur. Jeder Knoten "weiß" quasi, dass links nur kleinere Werte existieren und rechts nur größere oder gleich große. Man muss keine neue Mitte mehr berechnen und auch die Links- und Rechts-Variablen nicht mehr neu berechnen.

Der größte Vorteil eines binären Suchbaums liegt aber beim Einfügen und Löschen von Elementen.

Ein binärer Suchbaum
Autor: Ulrich Helmich, erstellt von Mistral Vibe nach den Vorgaben des Autors.

Schauen wir uns diesen Baum noch einmal an. Wir wollen die 8 einfügen.

1. Dazu fangen wir bei der Wurzel an: Die 8 ist kleiner als die 32, also müssen wir die 8 in den linken Teilbaum einfügen - das ist die erste Operation.
2. Die 8 ist kleiner als die Wurzel des linken Teilbaums, die 14, daher müssen wir die 8 in den linken Teilbaum der 14 einfügen - Operation Nr. 2
3. Nun ist die 8 größer als die 6, die Wurzel dieses Teilbaums, daher machen wir rechts weiter - Operation 3.
4. Dort sehen wir die 9 als Wurzel, und machen wieder links weiter - Operation 4.
5. Die Wurzel des linken Teilbaums ist die 7. Bei diesem Knoten handelt es sich um ein sogenanntes Blatt, da der Knoten keine Nachfolger mehr besitzt. Wir hängen die 8 jetzt einfach als rechten Nachfolger an die 7 an, und fertig ist der erweiterte binäre Suchbaum - Operation 5.

Mit nur fünf Operationen haben wir also die 8 in die Datenstruktur eingefügt. Bei einem Array hätten wir wesentlich mehr Operationen dafür gebraucht.