Zunächst etwas Theorie
Zellulärer Automat
Ein Zellulärer Automat ist ein 4-Tupel Z = (R, N, Q, δ), dabei ist
R = ein Raum (z.B. eine zweidimensionale Matrix)
N = eine endliche Nachbarschaft (z.B. die vier Nachbarzellen links, rechts, oben, unten)
Q = eine endliche Zustandsmenge (z.B. { gesund, krank, tot } )
δ = eine Überführungs-Funktion.
Diese Definition hört sich recht theoretisch an. Aber wenn wir ein einfaches Beispiel betrachten, wird relativ schnell klar, was sich dahinter verbirgt. Betrachten Sie folgende Abbildung:
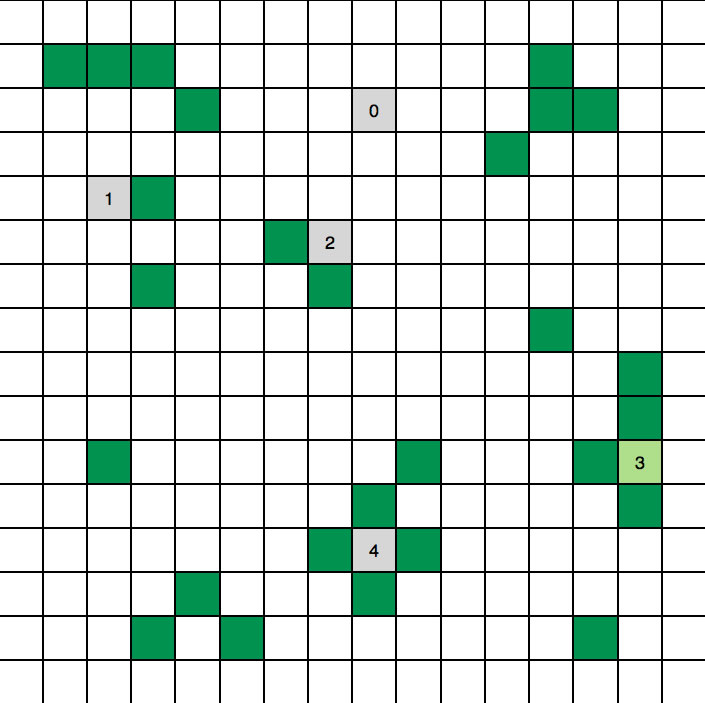
Ein zellulärer Automat
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende.
In der Abbildung sehen wir einen zellulären Automaten mit 16 x 16 Zellen, die in je zwei Zuständen vorkommen können, lebendig (grün) und tot (weiß). Jede Zelle hat genau vier Nachbarzellen. Bei fünf Zellen des Automaten wurde die Zahl der lebenden Nachbarzellen notiert.
Damit hätten wir die Komponenten R, N und Q dieses Zellulären Automaten schon einmal näher beschrieben:
R = der abgebildete "Raum" aus 16 x 16 Zellen.
N = die vier Nachbarn der betrachteten Zelle.
Q = der Zustand der betrachteten Zelle {lebendig, tot} bzw. {0, 1}.
Es bleibt nur noch die Übergangs-Funktion δ. Am anschaulichsten stellt man δ als Tabelle dar:
| Lebende Nachbarn | Neuer Zustand |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 0 |
| 4 | 0 |
Alternativ könnte man δ auch rein verbal definieren:
"Wenn eine Zelle keine lebenden Nachbarn hat, soll sie im nächsten Zyklus tot sein. Hat eine Zelle einen oder zwei lebende Nachbarn, so soll sie im nächsten Zyklus lebendig sein. Bei drei oder vier lebenden Nachbarn soll eine Zelle im nächsten Zyklus tot sein."
Bei dieser Übergangsfunktion hängt der Zustand im nächsten Zyklus nur von der Zahl der lebenden Zellen im aktuellen Zyklus ab, nicht aber vom Zustand der Zelle selbst. Das wäre dann ebenfalls eine Übergangsfunktion, aber eine kompliziertere. Man könnte diese kompliziertere Übergangsfunktion mit einer dreispaltigen Tabelle definieren, wobei die neue Spalte den aktuellen Zustand darstellt.
Schauen wir uns nun an, welche Auswirkungen diese Übergangs-Funktion auf die Verteilung der Zellen im Raum hat.
Betrachten wir zunächst die mit der Ziffer "0" markierte Zelle in der Abbildung 9.3 - 1. Diese tote Zelle hat keine lebenden Nachbarn, also wird ihr Zustand in der nächsten Generation wieder "tot" sein. Die mit der Ziffer "1" gekennzeichnete Zelle wird in der nächsten Generation den Zustand 1 oder "lebendig" haben, ebenso die mit der Ziffer "2" gekennzeichnete Zelle. Die lebende Zelle mit der Ziffer "3" wird sterben, und die tote Zelle "4" wird wegen ihrer vier lebenden Nachbarn in dem Zustand "tot" verbleiben.
Berechnung der nächsten Generationen↑
Der zelluläre Automat berechnet jetzt für jede einzelne Zelle mithilfe der Übergangs-Funktion den Folgezustand in der nächsten Generation, realisiert diesen neuen Zustand aber erst dann, wenn er mit der letzten Zelle fertig ist. Somit hängt der Zustand einer Zelle ausschließlich vom aktuellen Zustand der Nachbarzellen ab, und nicht vom bereits errechneten Folgezustand. Schauen wir uns das mal für ein sehr kleines Beispiel an:
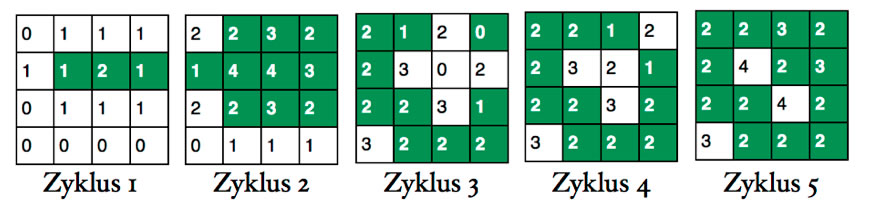
Berechnung der Folgezustände über fünf Zyklen
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende.
Die Zahlen in den Kästchen zeigen die Anzahl der jeweils lebenden Nachbarn. In dem ersten Zyklus haben sieben tote Zellen genau einen Nachbarn. Diese sieben Zellen werden im zweiten Zyklus dann lebendig sein. Die drei lebendigen Zellen des ersten Zyklus haben einen oder zwei lebende Nachbarn, laut Übergangsfunktion werden diese Zellen im zweiten Zyklus ebenfalls lebendig sein.
Im zweiten Zyklus leben zehn Zellen, und nur sechs Zellen sind noch tot. Mit drei oder vier lebenden Nachbarn ist man im nächsten Zyklus tot (weil das Gedränge einfach zu groß ist…), daher sterben fünf von den lebenden Zellen im dritten Zyklus ab. Umgekehrt werden fünf bisher tote Zellen wieder lebendig, weil sie einen oder zwei lebende Nachbarn haben.
Und so geht das immer weiter, über eine beliebige Anzahl von Zyklen.
Eine Torus-Welt↑
Bei der Berechnung der Nachbarschaft sind die Randzellen und die Eckzellen problematisch. Randzellen haben drei, Eckzellen sogar nur zwei Nachbarn. Entweder muss dies bei der Übergangs-Funktion berücksichtigt werden, was diese natürlich enorm verkompliziert, oder es muss in die geometrische Trickkiste gegriffen werden. Wir "verkleben" einfach den linken Rand unserer Welt mit dem rechten Rand, so dass wir einen Zylinder erhalten. Und jetzt wird es kompliziert: Wir verkleben den oberen Rand des Zylinders mit dem unteren Rand. So erhalten wir einen sogenannten Torus:

Ein Torus
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende.
Einen Torus kennen Sie sicherlich aus dem Alltag: Ein Fahrradschlauch oder ein Reifen ist im Grunde auch ein Torus. In unserer Torus-Welt hat jetzt jedes Feld vier Nachbarn. Randfelder und Eckfelder gibt es nicht mehr.
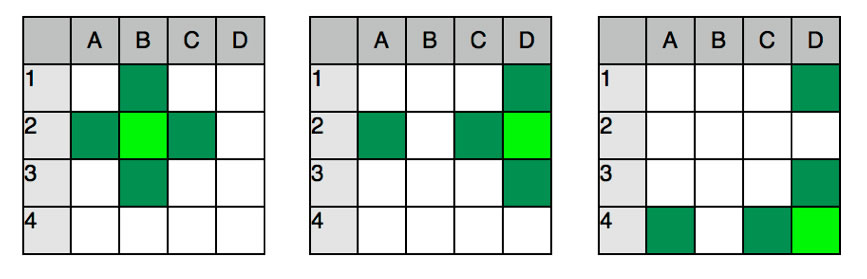
Berechnungen bei einer Torus-Welt
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende.
Wir wollen jetzt einen solchen Zellulären Automaten mithilfe eines Java-Applets simulieren. Dabei wollen wir eine Matrix aus 100 x 100 Zellen mit zwei Zuständen zu einer Torus-Welt zusammenfügen, die Zellen mit dem Zufallsgenerator initialisieren und dann mithilfe eines Buttons die Folgegenerationen erzeugen und zeichnen lassen.
Workshop: Eine zweidimensionale Torus-Welt↑
Den eigentlichen Workshop habe ich in die nächste Seite ausgelagert.