Eine ganz einfache, intuitive Methode
Wenn man einen Informatik-Kurs bittet, sich eine einfache Methode zur Lösung des TSP auszudenken, kommen ca. 50% der Schüler auf die folgende Idee, die in der Literatur als Nearest neighbour-Methode (Methode des nächsten Nachbarn; im amerikanischen Englisch übrigens nearest neighbor) bekannt geworden ist.
Die nearest neighbour-Methode
Wir beginnen mit der ersten Stadt der Liste, nennen wir sie einfach "A".
Wir suchen nun nach der Stadt, die A am nächsten ist. Dazu verwendet man am besten eine Entfernungstabelle, die man sich vorher angefertigt hat.
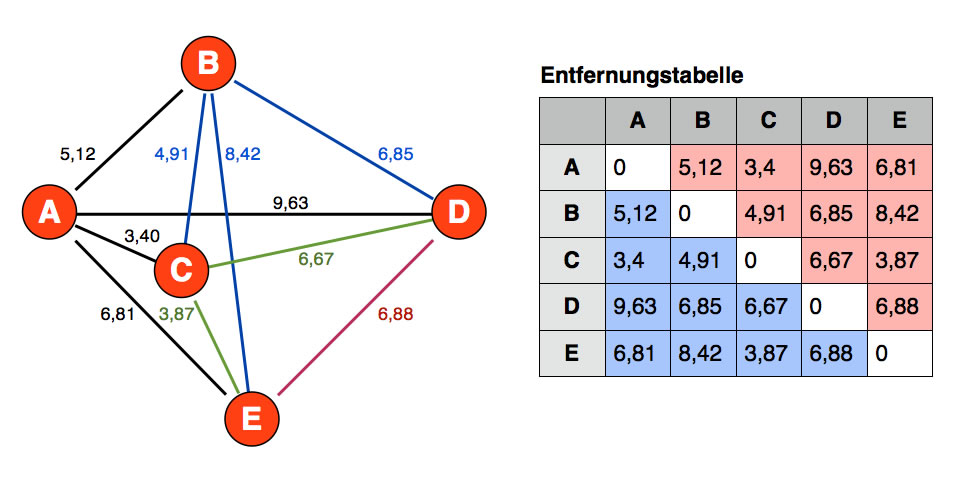
Eine Entfernungstabelle für fünf Städte
Autor: Ulrich Helmich, Lizenz: siehe Seitenende
Man kann den Algorithmus allerdings auch ohne eine solche Tabelle schreiben, dann muss man allerdings bei jedem Durchgang die Entfernungen neu berechnen, was wertvolle Rechenzeit kosten kann.
Wir sehen sofort, dass C die Stadt ist, die A am nächsten liegt.
Dasselbe machen wir jetzt für C. Die nächste Stadt ist A, aber A ist ja bereits in der Tour, scheidet als möglicher Kandidat also aus. Die C am nächsten liegende "freie" Stadt ist dann E. Also haben wir jetzt die Tour A - C - E. Nur B und D liegen noch nicht in der Tour. Die nächste Stadt ist dann D, und von hier geht es nach B, und von dort zurück nach A:
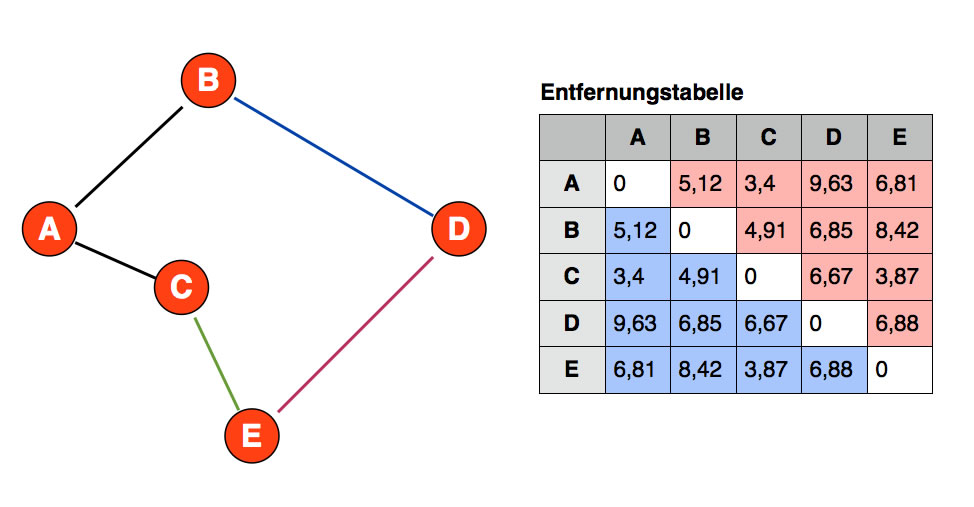
Die gefundene kurze Tour
Autor: Ulrich Helmich, Lizenz: siehe Seitenende
Hier sehen wir die auf diese Weise gefundene Tour. Ob sie wirklich die kürzeste Tour ist, kann man bei fünf Städten noch relativ leicht überprüfen. Bei ein großen Anzahl von Städten ist das nicht mehr so leicht, man müsste dann eigentlich wieder die Brute-force-Methode laufen lassen, um die kürzeste Tour zu finden.
Quicktime-Film zur Demonstration der NN-Methode für 21 Städte
Autor: Ulrich Helmich, Lizenz: siehe Seitenende
Hier sehen Sie den Screenshot eines Quicktime-Films, der den nearest-neighbour-Algorithmus für 21 Städe zeigt. Den Film selbst können Sie sich hier herunter laden: Download (450 kB).
Der nearest-neighbour-Algorithmus in Java
Ich muss gleich am Anfang sagen, dass ich mit dem von mir selbst entwickelten Algorithmus noch nicht zu 100% zufrieden bin, aber egal, er soll Ihnen nicht vorenthalten werden...