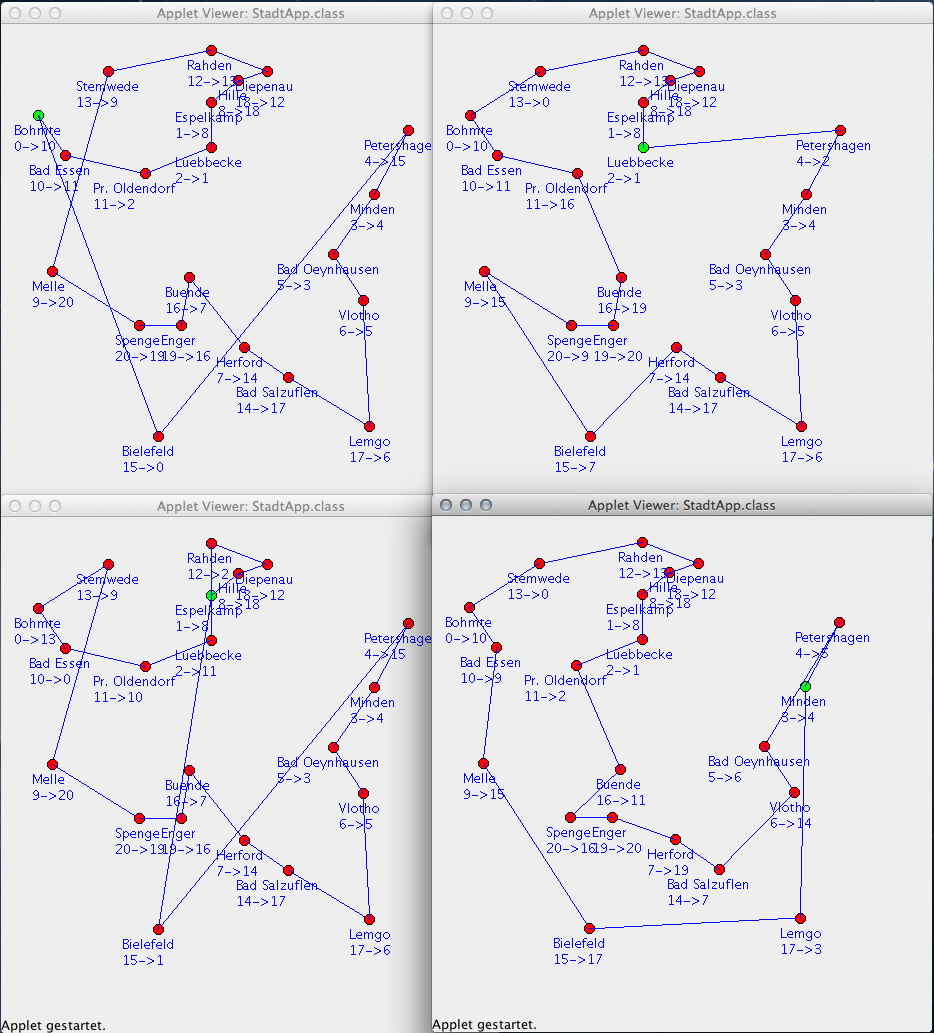
Vier Lösungen des 21-Städte-Problems
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende
Dieser Screenshot zeigt vier verschiedene Lösungen des 21-Städte-Problems. Jedes Mal wurde eine andere Anfangsstadt gewählt. Dazu musste die Methode nearestneighbour() leicht umgeschrieben werden:
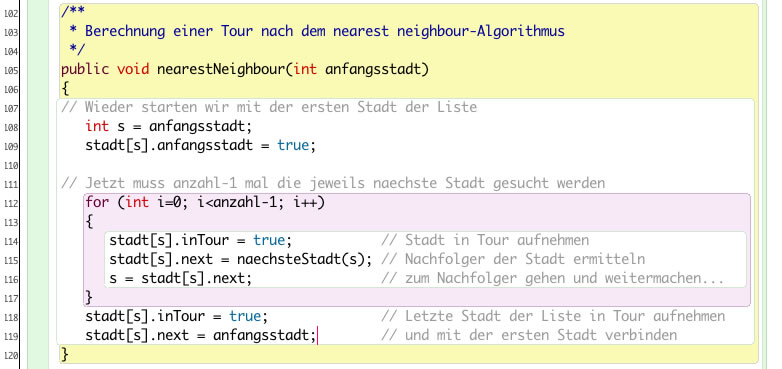
Die neue Version der Methode
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende
Die Klasse Stadt wurde um ein boolean-Attribut anfangsstadt erweitert, so dass die erste Stadt der Tour im Applet grün gezeichnet werden kann.
Man kann an den vier Screenshots gut erkennen, dass die erste Tour mit der Anfangsstadt 0 (Bohmte) tatsächlich noch verbessert werden kann. Die Tour mit der Anfangsstadt Lübbecke sieht viel kürzer aus.
Also besteht die Optimierung des nearest neighbour-Algorithmus darin, dass man nacheinander jede Stadt zur Anfangsstadt macht und dann die kürzeste ermittelte Route als Tour nimmt.
Dazu braucht man eine Methode gesamtlaenge, welche die Gesamtlänge einer Tour ermittelt. Eine solche Methode ist schnell geschrieben.
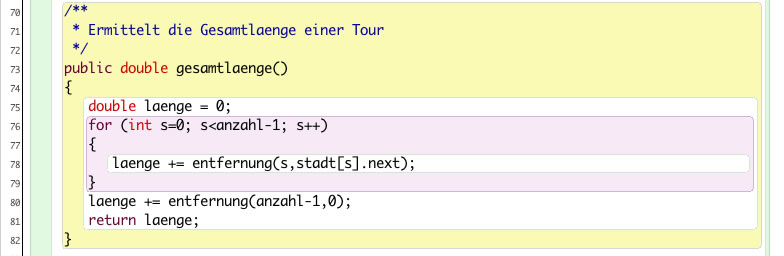
Die Methode gesamtlaenge()
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende
Dann brauchen wir eine Methode, die alle möglichen Touren ausprobiert und dann die kürzeste Tour von allen möglichen ermittelt:
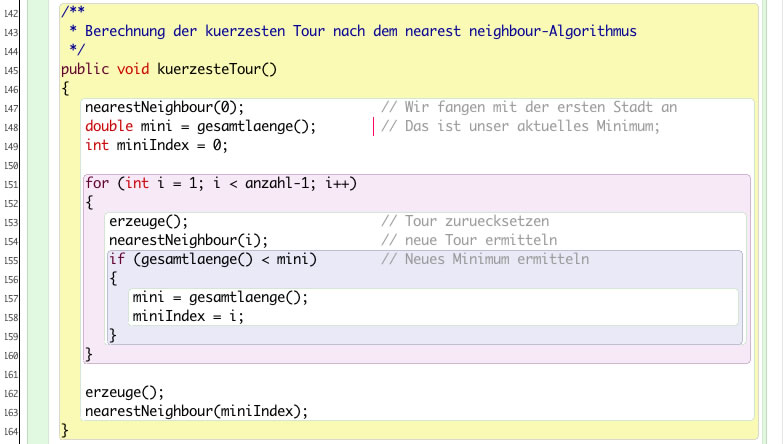
Die Methode kuerzesteTour()
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende
Schon ist das Problem gelöst und wir finden eine recht kurze Tour:
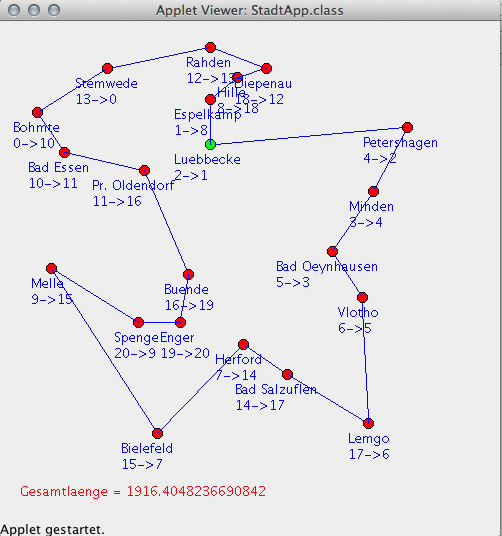
Ausgabe der kürzesten Tour
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende
Dies ist die kürzeste Tour, die nach dem nearest neighbour-Algorithmus möglich ist.
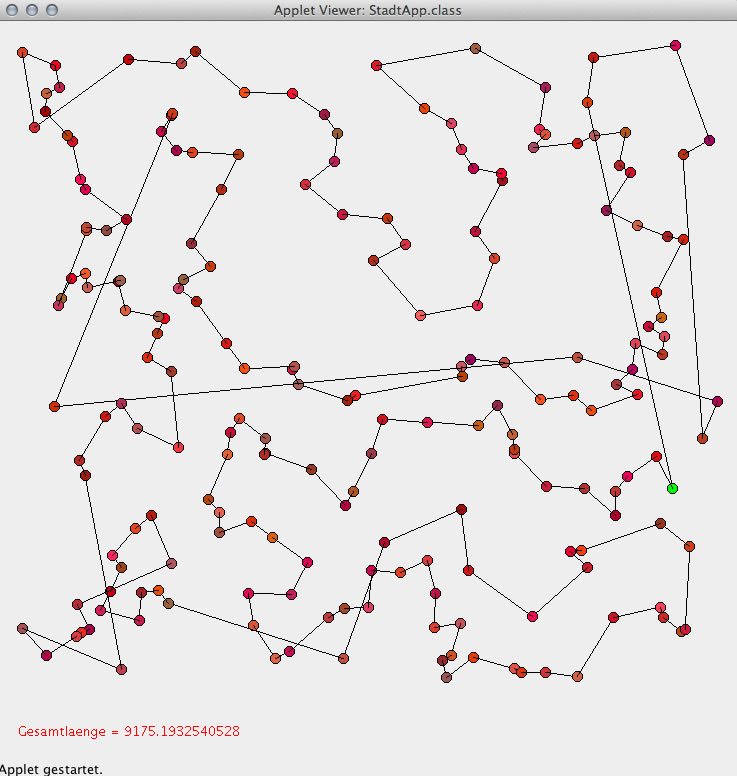
Eine Tour durch 200 Städte
Autor: Ulrich Helmich 2016, Lizenz: siehe Seitenende
Hier wurde der optimierte Algorithmus auf 200 Zufallsstädte (x- und y-Position wurden zufällig generiert) angewandt, das Ergebnis ist ganz passabel.
Weitere Optimierungen
Eine weitere Optimierungsmöglichkeit würde darin bestehen, Überschneidungen in den Touren zu entfernen. Nach Sedgewick kann man solche Überschneidungen zweier Teilstrecken entfernen, indem man Städte in der Tour tauscht. Eine Implementierung dieses Verfahrens im Informatik-Unterricht ist allerdings sehr aufwendig, vielleicht etwas für engagierte Schüler(innen) in einem Informatik-Leistungskurs. Zuerst einmal muss der Algorithmus ja Überschneidungen als solche erkennen. Dann muss er die Überschneidung beseitigen, ohne dafür aber eine neue Überschneidung zu erzeugen, was nämlich sehr leicht passiert.
Natürlich gibt es völlig andere Algorithmen zum Lösen des TSP, aber das sind dann keine Optimierungen des NN-Algorithmus mehr, sondern völlig eigenständige Algorithmen.