Beispiel Wasserstoff-Molekül
Die Molekül-Orbital-Theorie lässt sich am besten bzw. am einfachsten am Beispiel des H2-Moleküls erklären. Ein Wasserstoff-Molekül besteht aus zwei gleichen Atomen, nämlich zwei Wasserstoff-Atomen. Jedes Wasserstoff-Atom besitzt nur ein einziges Atom-Orbital, das 1s-Orbital, das mit nur einem Elektron besetzt ist.
Rückblick auf die Sekundarstufe II
Im Unterricht der Sekundarstufe II lernt man, dass sich die beiden "einfach besetzten Kugelwolken" der beiden H-Atome überlappen. So entsteht eine "gemeinsame Kugelwolke", die mit zwei Bindungselektronen besetzt ist. Diese beiden Bindungselektronen halten sich zwischen den positiv geladenen Atomkernen auf und halten diese Atomkerne so zusammen. Ohne diesen negativen "Elektronenkitt" würden sich die beiden Atomkerne abstoßen.
Das H2-Molekül nach der MO-Theorie
Nach der MO-Theorie überlappen die beiden 1s-Orbitale der beiden H-Atome, man sagt auch, sie kombinieren. Durch die Kombination dieser beiden Orbitale entstehen zwei Molekülorbitale (MOs), ein bindendes und ein anti-bindendes. Das bindende MO hat eine niedrigere Energie als die beiden 1s-Orbitale der H-Atome, während das anti-bindende ein höheres Energieniveau hat als die 1s-Orbitale der H-Atome. Graphisch kann man das so darstellen:
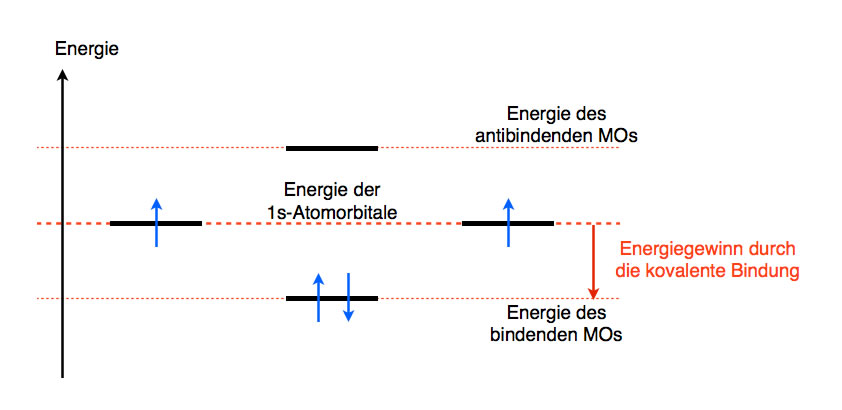
Die beiden Molekülorbitale des Wasserstoff-Moleküls
Autor: Ulrich Helmich 11/2024, Lizenz: Public domain.
Wieso gibt es überhaupt ein bindendes und ein anti-bindendes Molekülorbital?
Nach der gängigen Vorstellung der Quantenchemie kann man Elektronen nicht nur als Teilchen betrachten, sondern auch als Wellen. Das ist zwar für den normalen Menschenverstand schwer vorstellbar, aber was soll's; Physiker haben damit kein Problem. Nach dieser abstrakten Vorstellung sind Elektronen allerdings keine normalen (eindimensionalen) Wellen, sondern dreidimensionale.
Um uns das besser klar zu machen, stellen uns jetzt erst einmal zwei normale eindimensionale Wellen vor:
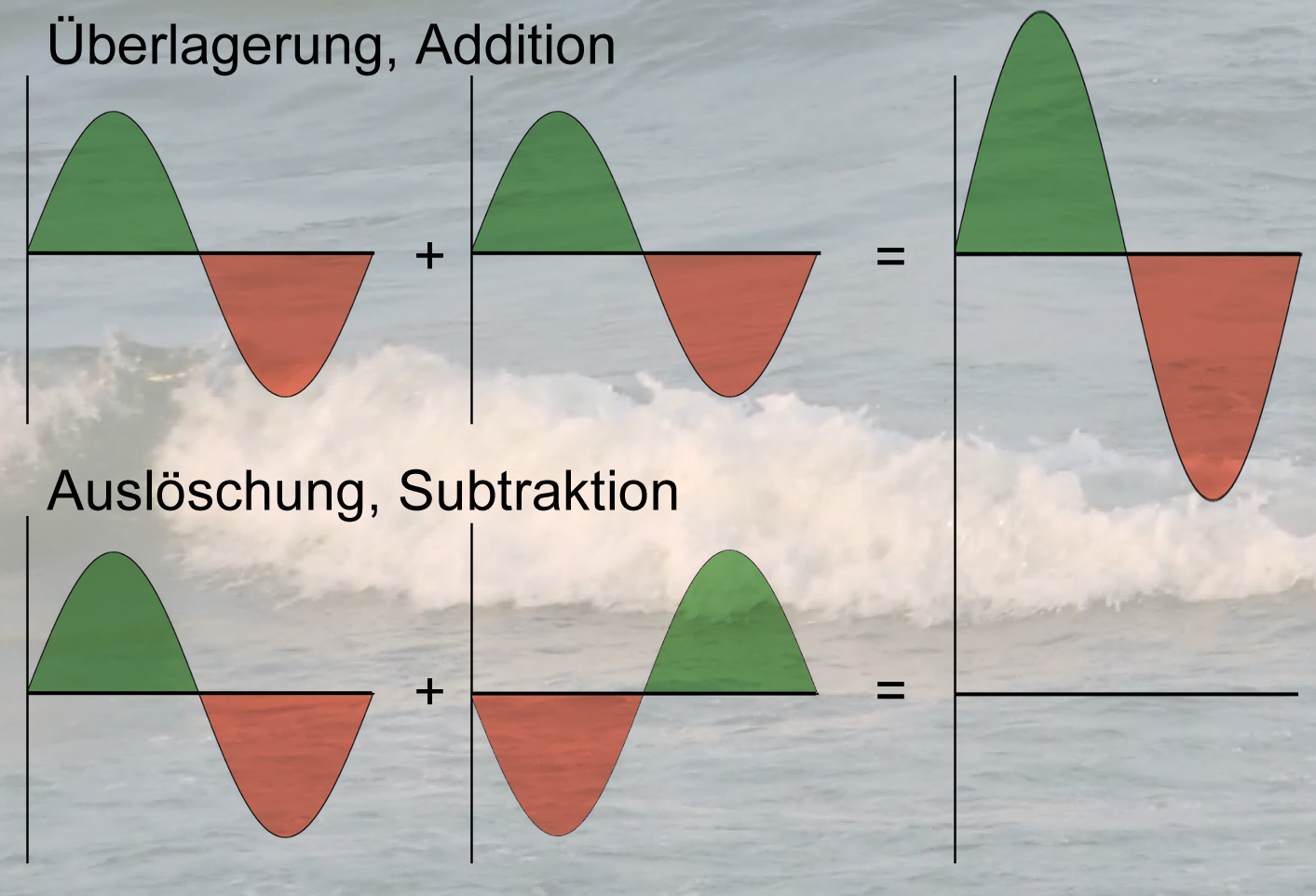
Die Überlagerung von zwei eindimensionalen Wellen ist auf zwei Weisen möglich
Autor: Ulrich Helmich 2023, Lizenz: Public domain.
Zwei eindimensionale Wellen können sich auf verschiedene Weisen gegenseitig überlagern. Dabei sind zwei Extremfälle zu unterscheiden.
Überlagerung, Addition
Im ersten Extremfall überlagern sich die Wellen so, dass die Wellenberge der einen Welle exakt auf die Wellenberge der anderen Welle treffen. Die beiden Wellen addieren sich, es entsteht eine neue Welle mit doppelt so großer Amplitude (Höhe der Wellenberge).
Auslöschung, Subtraktion
Das andere Extrem liegt dann vor, wenn der Wellenberg der einen Welle exakt auf ein Wellental der anderen Welle trifft. Haben beide Wellen die gleiche Wellenlänge und Amplitude, dann löschen sich die beiden Wellen gegenseitig aus.
Dieses Phänomen nutzt man übrigens technisch aus bei der Konstruktion von noise-chancelling-Kopfhörern. Ein Mikrophon nimmt die Geräusche aus der Umgebung auf. Dann werden die Schallwellen um genau eine halbe Wellenlänge "verschoben" und dem Hörer über die Kopfhörer eingespielt. Die "echten" Schallwellen, die den Kopfhörer durchdringen, werden dann von diesen phasenverschobenen Wellen ausgelöscht.
Atomorbitale muss man sich wie dreidimensionale Wellen vorstellen. Auch Atomorbitale können sich gegenseitig verstärken oder auslöschen. Bei der Bildung der bindenden Molekülorbitale verstärken sich die beiden 1s-Orbitale der H-Atome gegenseitig, und bei der Bildung der anti-bindenden MOs löschen sich die beiden Atomorbitale gegenseitig aus.
Die Energie des bindenden MOs liegt unter der Energie der beiden Atomorbitale. Daher wird dieses MO bevorzugt von den beiden Elektronen besetzt. Die resultierende kovalente Bindung (s-s-Überlappung) ist daher energieärmer und somit energetisch günstiger als der Zustand der nicht-verbundenen Atome.
Beispiel Ethen-Molekül
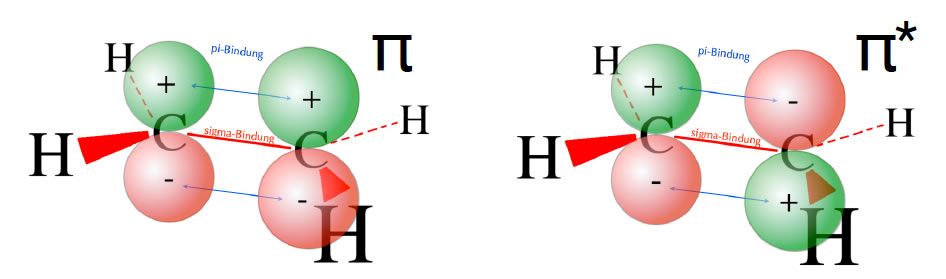
Die beiden pi-Molekülorbitale des Ethens
Autor: Ulrich Helmich 2020, Lizenz: Public domain.
Auch bei größeren Molekülen kann man die MO-Theorie anwenden. Betrachten wir als Beispiel das Ethen-Molekül. Um nicht die Übersicht zu verlieren, konzentrieren wir uns dabei auf die beiden pz-Orbitale der sp2-hybridisierten C-Atome des Ethens.
Achten Sie auf die Ausrichtung der pz-Orbitale. Links in der Abbildung befinden sich die beiden grün gefärbten Orbitallappen "oben" im Molekül. Wenn die pz-Orbitale so ausgerichtet sind, addieren sich die "Wellenberge" der dreidimensionalen Wellen, und es entsteht ein bindendes Molekülorbital. So entsteht die normale pi-Bindung zwischen den beiden C-Atomen.
Rechts in der Abbildung sind die beiden pz-Orbitale jedoch entgegengesetzt ausgerichtet. Beim linken C-Atom zeigt der grüne Lappen (der Wellenberg) nach oben, beim rechten C-Atom aber nach unten. Wenn die pz-Orbitale so ausgerichtet sind, findet quasi eine Subtraktion der dreidimensionalen Wellen statt. So erklärt sich das Zustandekommen des anti-bindenden Molekülorbitals.
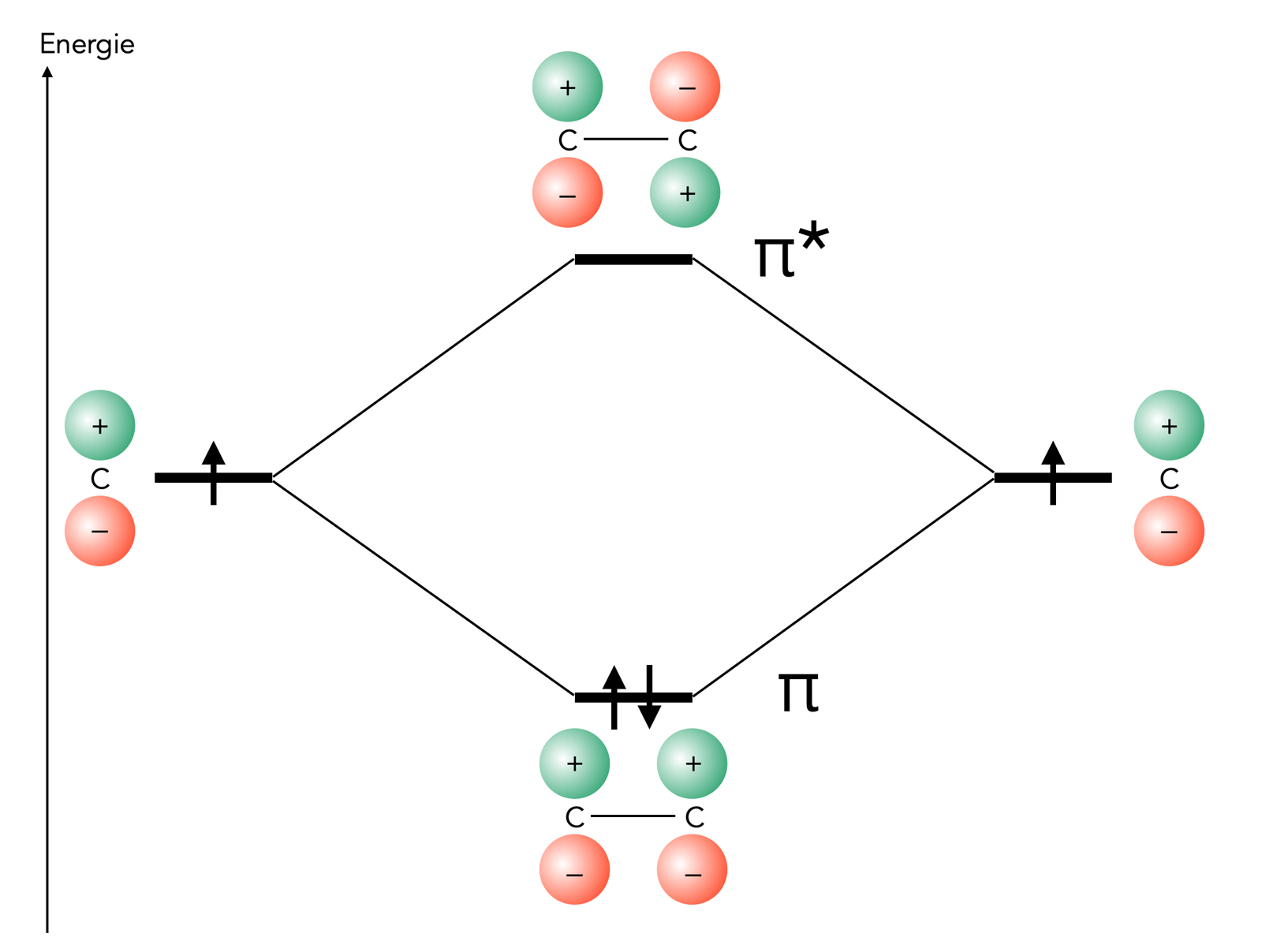
Die pi-Molekülorbitale der C=C-Doppelbindung
Autor: Ulrich Helmich 04/2023, Lizenz: Public domain
Das obige Bild zeigt die beiden π-MOs der C=C-Doppelbindung und ihre Energieniveaus. Ganz links und ganz rechts sehen wir die Energieniveaus der freien pz-Orbitale eines sp2-hybridisierten C-Atoms. In der Mitte unten ist das bindende π-MO der Doppelbindung dargestellt, das normalerweise mit zwei Elektronen besetzt ist. Das Energieniveau dieses bindenden π-Orbitals liegt deutlich unter dem der freien pz-Orbitale. Das Eingehen der pi-Bindung bedeutet also einen Energiegewinn für beide C-Atome.
Oben in der Mitte sehen wir das anti-bindende π*-MO des Ethens, das normalerweise nicht mit Elektronen besetzt ist. Die Energie dieses π*-MOs ist deutlich höher als die Energie der freien pz-Orbitale.
Auf dieser Lexikon-Seite werden die Molekülorbitale der Allyl-Gruppe beschrieben und erläutert.
MO-Theorie und Farbstoffchemie
Ein Molekül wie Butadien hat vier dieser pz-Orbitale an benachbarten C-Atomen, so dass diese Orbitale überlappen können. Nun gibt es immer genau so viele MOs, wie pz-Orbitale beteiligt sind. Mit vier pz-Orbitalen erhalten wie also vier MOs, genauer gesagt, vier pi-MOs, denn die anderen MOs vernachlässigen wir in der Farbstoffchemie und überhaupt in der organischen Chemie. Von diesen vier MOs sind zwei bindend und zwei anti-bindend.
Auf dieser Lexikonseite beschreibe ich die vier MOs des Butadien-Moleküls sehr ausführlich mit vielen Zeichnungen
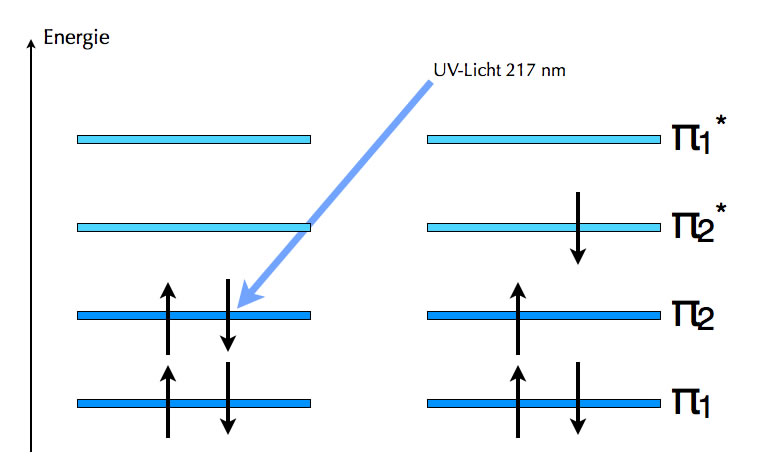
Die vier MOs des Butadien-Moleküls
Die vier Elektronen verteilen sich auf die vier MOs nach einem ganz einfachen Prinzip: Mit der Besetzung wird unten angefangen, und in jedes MO passen maximal zwei Elektronen. Daher ergibt sich der oben links dargestellte Zustand, dass nur die beiden bindenden pi-MOs besetzt sind. Durch Absorption von UV-Licht der Wellenlänge 217 nm kann aber eines der beiden Elektronen des oberen besetzten MOs in das untere noch nicht besetzte anti-bindende MO befördert werden. Weitere Einzelheiten dazu siehe die entsprechenden Seiten in der Farbstoffchemie.
Weitere Einzelheiten zur MO-Theorie der konjugierten Polyene siehe die entsprechenden Seiten in der Farbstoffchemie-Abteilung.