Ein Gedankenexperiment mit Ratten
Machen wir mal wieder ein Gedankenexperiment (wie so oft auf diesen Webseiten):
In einem großen Raum werden 100 Ratten ausgesetzt, 50 Männchen und 50 Weibchen. Der Raum ist gut belüftet, die Tiere bekommen ausreichend Wasser, und für Futter ist gesorgt, allerdings bleibt die pro Tag zur Verfügung stehende Wasser- und Futtermenge konstant. Wenn sich also die Ratten vermehren, wird nicht mehr Wasser oder Futter zur Verfügung gestellt als zu Beginn des Versuchs.
Wie wird die Bevölkerungsentwicklung unter diesen Umständen aussehen?
Zu Beginn des Experiments ist für die wenigen Ratten viel Wasser und Futter vorhanden. Die Tiere können sich optimal vermehren. Also setzt ein exponentielles Bevölkerungswachstum ein.
Wenn die Populationsdichte der Ratten stark zugenommen hat, wird es langsam knapp mit Wasser und Nahrung, denn die zur Verfügung stehende Menge dieser Ressourcen wurde bei dem Experiment ja nicht erhöht. Diese Knappheit der Ressourcen sollte sich in einer gesteigerten Sterberate und einer verminderten Geburtenrate niederschlagen. Die Wachstumsrate der Population sinkt, und die Populationsdichte steigt nicht mehr so stark an. Das exponentielle Wachstum geht in ein lineares Wachstum über.
Die Population wächst weiter, aber die Ressourcen werden immer knapper, der "Kampf ums Überleben" wird immer härter. Innerartliche Konkurrenz, Stress, Krankheiten etc. nehmen zu, die Sterberate steigt weiter an, die Geburtenrate sinkt immer mehr. Das lineare Wachstum geht in eine Stagnation über, die Wachstumsrate nähert sich dem Wert Null, die Bevölkerungszahl bleibt konstant, unter Umständen geht die Populationsdichte sogar wieder zurück (negative Wachstumsrate).
Logistisches Wachstum
Stellen wir das Wachstum der Rattenbevölkerung einmal graphisch dar, so erhalten wir folgende Kurve:
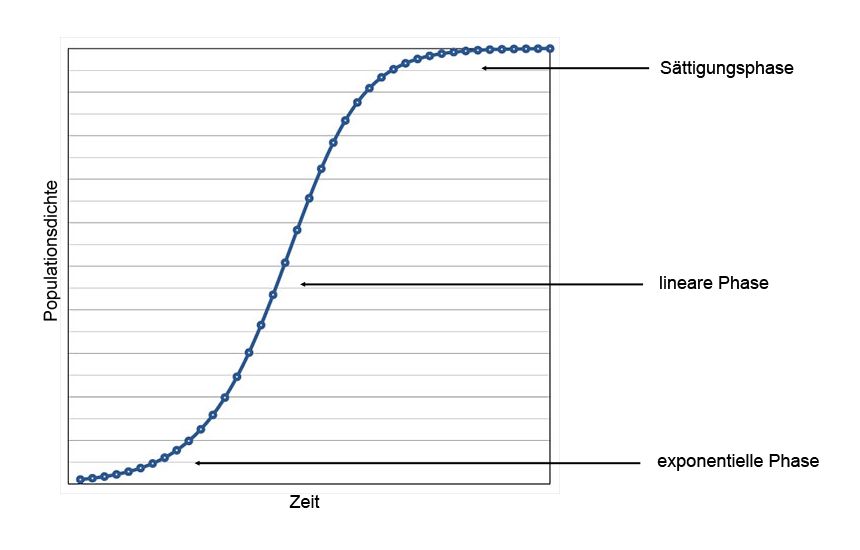
Wachstum der Rattenbevölkerung
Auf der x-Achse ist der zeitliche Verlauf zu sehen, auf der y-Achse die Populationsdichte. Hier sind jetzt ganz bewusst keine Einheiten eingetragen, um den abstrakten bzw. theoretischen Charakter der Kurve zu unterstreichen.
Gut zu erkennen sind aber die drei Phasen, die ich Text beschrieben wurden. Das Populationswachstum startet mit einer exponentiellen Phase, die dann in eine lineare Phase (Mitte des Graphen) übergeht. Ganz am Ende nimmt der Graph die Form einer Sättigungskurve an und geht in die stationäre Phase über.
Eine solche Wachstumskurve wird als logistisch bezeichnet, und man spricht von einem logistischen Populationswachstum.
Gelegentlich wird eine logistische Wachstumskurve auch in vier oder fünf Phasen unterteilt; nach der linearen Phase könnte man zum Beispiel zunächst von einer Phase des verzögerten Wachstums sprechen, erst danach kommt die stationäre Phase. Manche Autoren sprechen auch von einer lag-Phase ganz zu Beginn des Populationswachstums. Wenn die Populationsdichte sehr gering ist, ist die Geburtenrate sehr niedrig, weil es kaum zur innerartlichen Begegnung zwischen den Geschlechtern kommt, daher entwickelt sich die Bevölkerung zunächst sehr langsam.
Sehr empfehlenswert ist hier das Video "Logistisches Wachstum einfach erklärt" von TheSimpleMaths auf YouTube.
Mathematik des logistischen Wachstums
$\frac{dN}{dt} = k\times N$
Dies war die Differentialgleichung für das exponentielle Wachstum, wie sie bereits vor der vorherigen Seite erklärt wurde. Dabei ist $k$ die Wachstumsrate und $N$ die aktuelle Zahl der Individuen. Die Gleichung besagt folgendes: Je größer die Zahl der Individuen $N$, desto größer die zeitliche Zunahme $\frac{dN}{dt}$ der Population.
Schauen wir uns nun die entsprechende Differentialgleichung für das logistische Wachstum an:
$\frac{dN}{dt} = k\times (\frac{K-N}{K}) \times N$
Falls Ihr Browser die Formeln auf dieser Seite nicht korrekt darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist Ihr Browser veraltet, oder Sie haben im Augenblick keine Internetverbindung.
Neu hinzugekommen ist der Ausdruck in der Klammer. K steht dabei für die Umweltkapazität. Darunter versteht man die Anzahl der Individuen oder die Dichte der Individuen, die unter den gegebenen Umweltbedingungen in dem gegebenen Lebensraum maximal existieren können.
$K-N$ ist nun quasi der "Platz", der noch für weiteres Wachstum zur Verfügung steht. Wenn die Population wächst, wird die Differenz $K-N$ immer kleiner, damit wird auch der Klammerausdruck immer kleiner, und die zeitliche Zunahme $\frac{dN}{dt}$ wird ebenfalls immer kleiner. Die eigentliche Wachstumsrate $k$ bleibt allerdings konstant - der Begriff "Wachstumsrate" trifft hier strenggenommen nicht mehr zu. Gilt schließlich $N = K$ (die Kapazität der Umwelt ist also ausgeschöpft), hat der Klammerausdruck den Wert 0 und somit ist auch die zeitliche Zunahme $\frac{dN}{dt} = 0$. Das Populationswachstum stagniert.
Methodentraining Tabellenkalkulation II
Bereits bei der Besprechung des exponentiellen Wachstums hatten wir gelernt, wie man mit Hilfe einer Tabellenkalkulation ein solches Wachstum simulieren kann. Bei der Simulation des logistischen Wachstums können wir auf diesen Kenntnissen aufbauen.
In die erste Spalte (A) einer neuen Tabelle tragen wir wieder die Generationen ein. In die Zelle B2 kommt wieder die Start-Anzahl der Individuen, nämlich 100. In die Zelle D2 tragen wir die Wachstumsrate ein (0,25), und in die Zelle E2 die Kapazität der Umwelt (10.000).
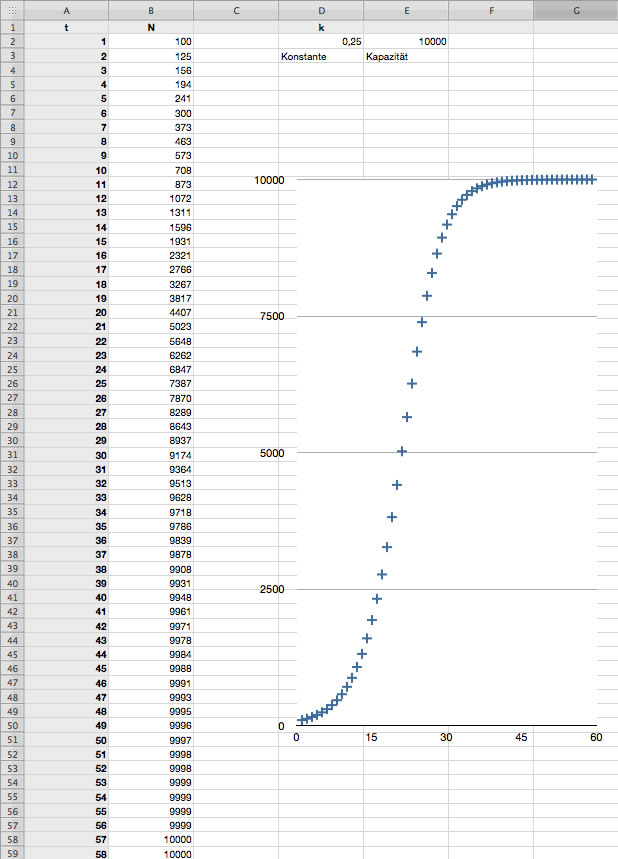
Simulation logistischen Wachstums mit einer Tabellenkalkulation (Numbers)
Die Differentialgleichung für das logistische Wachstum
$\frac{dN}{dt} = k\times (\frac{K-N}{K}) \times N$
wird in folgende Formel für die Zelle B3 umgewandelt:
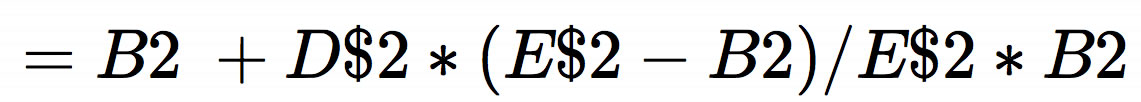
Formel für die Tabellenkalkulation
Leider musste ich hier die Formel für die Tabellenkalkulation in eine Graphik einbetten, weil das MathJax-Plugin auf dieser Webseite die Dollarzeichen falsch interpretiert. Die Dollarzeichen sind wichtig, damit die Formel auch in den darunterliegenden Zellen stets auf die Zellen D2 und E2 zugreift und nicht auf die unter D2 und E2 liegenden Zellen, in denen dann keine Werte mehr stehen.
Das ist der Vorteil des Arbeitens mit Differentialgleichungen, man kann sie leicht in die Formel für eine Tabellenkalkulation umwandeln.
Tatsächliches Populationswachstum
Nach diesen ganzen theoretischen Betrachtungen stellt sich die Frage, ob Populationen unter natürlichen Bedingungen ebenfalls logistisch wachsen.
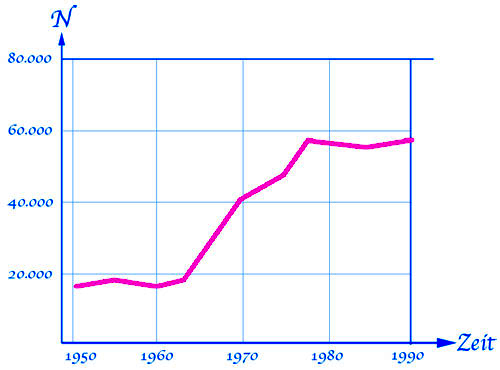
Wachstum einer Vogelpopulation in Bayern
Quelle:
Bayrisches Landesamt für Umwelt, Seite "Komoranmanagement"
Hier sehen wir ein typisches Beispiel für "echtes" logistisches Wachstum. Dargestellt ist das Wachstum einer Vogelpopulation in Bayern. Die Übergänge zwischen den drei Phasen des Populationswachstums sind nicht so schön zu sehen wie in der Theorie, aber mit viel Phantasie kann man eine logistische Kurve in den tatsächlichen Graphen legen.
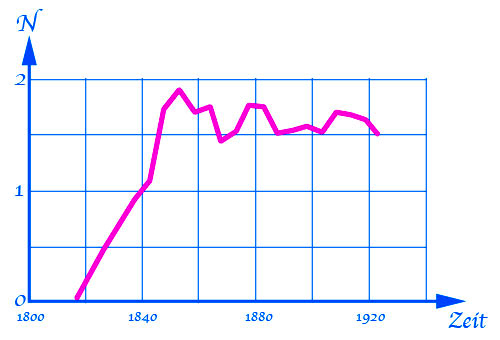
Wachstum einer Schafspopulation auf Tasmanien
Dies ist das berühmte Beispiel der Schafe in Tasmanien. Die Zahlen auf der y-Achse bedeuten Millionen. Auch hier kann man sich mit viel Phantasie eine logistische Wachstumskurve denken.
Wir sehen also: tatsächliches logistisches Wachstum ähnelt im Prinzip weitgehend ungefähr dem theoretischen Modell, es kommt aber zu teils starken Abweichungen.
In der Natur wachsen Populationen nur dann exponentiell, wenn genügend Ressourcen (Nahrung, Wasser, Luft etc.) zur Verfügung stehen. Mit steigender Populationsdichte N werden diese Ressourcen jedoch knapp, und die zeitliche Zunahme bzw. das Wachstum dN/dt der Population sinkt. Das Populationswachstum geht zunächst in lineares Wachstum über, und mit weiter sinkendem Wachstum nähert sich die Populationsdichte N einem Sättigungswert K, der als Kapazität der Umwelt bezeichnet wird.
