
Ein junger Mann sortiert seine CDs
Das Bild wurde von Photoshop 2025 generiert
Sortieren
Sortieren ist einer der häufigsten Prozesse in der praktischen Informatik und eines der interessantesten Themen in der theoretischen Informatik. Warum ist das Sortieren überhaupt so wichtig?
Der Grund dafür, dass in der Informatik ständig sortiert wird, liegt daran, dass ständig etwas gesucht wird. In einer CD-Sammlung sucht man einen bestimmten Titel, oder man sucht die CD, die man zum letzten Geburtstag von seiner Freundin geschenkt bekommen hat, oder man sucht ein bestimmtes Musikstück, von dem man genau weiß, dass man es hat. Hat man seine Songs auf dem PC oder Handy gespeichert, ist das Suchen meistens kein Problem.
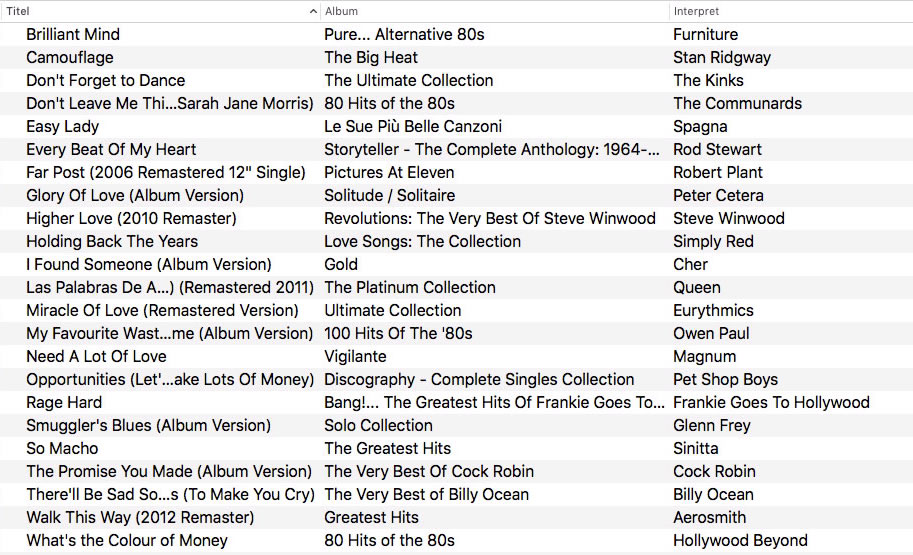
Ein Tabellenkalkulations-Dokument mit Songtiteln (Ausschnitt)
Autor: Ulrich Helmich 2022, Lizenz: Public domain.
Sucht man einen bestimmten Titel, klickt man in der Kopfzeile der Tabelle einfach auf "Titel" und das Programm sortiert die Playlist automatisch nach den Titeln, so wie auf dem Bild oben.
Genau so gut kann man auf "Album" oder "Interpret" klicken, und die Liste wird entsprechend sortiert. Das Suchen geht so natürlich viel schneller als bei einer völlig unsortierten Liste.
Suchen
Den bereits oben erwähnten Zeit-Aspekt wollen wir nun etwas näher untersuchen, und zwar an einem sehr viel einfacheren Beispiel. Betrachten wir dazu eine Liste aus zehn int-Zahlen.
Liste unsortiert:
| 20 | 3 | 5 | 12 | 17 | 4 | 9 | 2 | 13 | 8 |
Liste sortiert:
| 2 | 3 | 4 | 5 | 8 | 9 | 12 | 13 | 17 | 20 |
Beide Listen enthalten zehn Zahlen aus dem Bereich 1...20. Wir wollen nun die Zahlen 8, 9, 10, 11 und 12 in diesen beiden Listen suchen und dabei die Suchzeiten vergleichen. Als "Suchzeit" nehmen wir einfach die Anzahl der Vergleiche, die notwendig sind, die jeweilige Suchzahl zu finden.
| Suchzahl | Vergleiche unsortierte Liste |
Vergleiche sortierte Liste |
| 1 | 10 | 1 |
| 2 | 8 | 1 |
| 3 | 2 | 2 |
| 4 | 6 | 3 |
| 5 | 3 | 4 |
| Summe | 29 | 11 |
Um die Zahlen 1 bis 5 zu finden, benötigt man in unserer unsortierten Liste 29 Vergleiche, in der sortierten Liste dagegen nur 11 Vergleiche.
Eine kleine Optimierung
Wenn Sie in der Bibliothek vor einem Regel mit Romanen stehen und suchen nach einem Buch von Igor Zapparoni, dann werden Sie mit Sicherheit nicht ganz links beim Buchstaben 'A' mit der Suche anfangen, sondern ganz rechts beim Buchstaben 'Z'.
Auf ähnliche Weise könnte man den Such-Algorithmus optimieren. Angenommen, in der sortierten Liste sind Zahlen im Bereich zwischen 1 und 100 enthalten. Der Mittelwert liegt dann bei 50. Wenn Sie also Zahlen größer als 50 suchen, sollten Sie rechts mit der Suche anfangen. Bei Zahlen kleiner als 50 links.
Das folgende Programm können Sie sich in die Zwischenablage kopieren und dann ausgiebig testen:
import java.util.Random;
public class Aufgabe_8_1_1
{
int[] zahlen;
Random wuerfel;
public Aufgabe_8_1_1()
{
zahlen = new int[20];
wuerfel = new Random();
erzeugeArray();
ausgeben();
analyse();
}
public void erzeugeArray()
{
for (int i=0; i < zahlen.length; i++)
zahlen[i] = wuerfel.nextInt(100)+1;
}
public void sortiereArray()
{
Sorter.bubblesort(zahlen);
}
public int suchzeitVonLinksUnsortiert(int suchzahl)
{
for (int i=0; i < zahlen.length; i++)
if (zahlen[i] == suchzahl) return i;
return zahlen.length;
}
public int suchzeitVonLinksSortiert(int suchzahl)
{
for (int i=0; i < zahlen.length; i++)
if (zahlen[i] >= suchzahl) return i;
return zahlen.length;
}
public int suchzeitVonRechtsSortiert(int suchzahl)
{
for (int i=zahlen.length-1; i >=0; i--)
if (zahlen[i] <= suchzahl) return zahlen.length-i;
return zahlen.length;
}
public void analyse()
{
int sum;
int[] suchzahl = new int[10];
// Die 10 Suchzahlen in dem Array speichern
for (int i=0; i < 10; i++)
suchzahl[i] = wuerfel.nextInt(100)+1;
// 10 Zahlen suchen im unsortierten Array
sum = 0;
for (int n=0; n < 10; n++)
{
sum = sum + suchzeitVonLinksUnsortiert(suchzahl[n]);
}
System.out.println("Suchzeit für 10 Zahlen im unsortierten Array: " + sum);
// 10 Zahlen im sortieren Array suchen - nur von links
sortiereArray();
sum = 0;
for (int n=0; n < 10; n++)
{
sum = sum + suchzeitVonLinksSortiert(suchzahl[n]);
}
System.out.println("Suchzeit für 10 Zahlen im sortieren Array, von links: " + sum);
// 10 Zahlen in sortierten Array suchen - von links und rechts
sum = 0;
for (int n=0; n < 10; n++)
{
if (suchzahl[n] <= 50)
sum = sum + suchzeitVonLinksSortiert(suchzahl[n]);
else
sum = sum + suchzeitVonRechtsSortiert(suchzahl[n]);
}
System.out.println("Suchzeit für 10 Zahlen im sortieren Array, von links oder rechts: " + sum);
}
public void ausgeben()
{
for (int i=0; i < zahlen.length; i++)
System.out.println(i + "\t" + zahlen[i]);
}
}
Hier wird ein int-Array aus 20 Zahlen mit Zufallszahlen im Bereich 1..100 erzeugt. Die Methode
public int suchzeitVonLinksUnsortiert(int suchzahl)
{
for (int i=0; i < zahlen.length; i++)
if (zahlen[i] == suchzahl) return i;
return zahlen.length;
}
sucht nach der übergebenen Suchzahl in dem unsortierten Array und liefert die Position der gefundenen Zahl zurück, falls diese im Array enthalten ist. Andernfalls wird die Länge des Arrays als "Suchzeit" zurück geliefert.
Dann wird der Array sortiert, und zwar mit einem einfachen Bubblesort-Algorithmus. Die Klasse Sorter hat folgenden kurzen Quelltext:
public class Sorter
{
static private void tauschen(int[] zahl, int a, int b)
{
int temp = zahl[a];
zahl[a] = zahl[b];
zahl[b] = temp;
}
static public void bubblesort(int[] zahl)
{
for (int i=0; i < zahl.length; i++)
for (int j=0; j < zahl.length-1-i; j++)
if (zahl[j] > zahl[j+1])
tauschen(zahl,j,j+1);
}
}
Wie dieser Bubblesort genau funktioniert, wird in der nächsten Folge näher erklärt, Sie müssen sich jetzt noch nicht darum kümmern. Wichtig ist nur, dass Sie diese Klasse in Ihr BlueJ-Projekt mit einbinden, damit die Klasse Aufgabe_8_1_1 auf die Methode bubblesort() zugreifen kann.
Wenn der Array dann sortiert ist, kann die Methode suchzeitVonLinks etwas optimiert werden. Wenn die nächste Zahl im Array größer ist als die Suchzahl, kann die Suche abgebrochen werden. Die Suchzahl ist dann mit Sicherheit nicht in dem Array vorhanden. Hier der optimierte Quelltext der veränderten Methode:
public int suchzeitVonLinksSortiert(int suchzahl)
{
for (int i=0; i < zahlen.length; i++)
if (zahlen[i] >= suchzahl) return i;
return zahlen.length;
}
Theoretisch könnte man hier auf die letzte Zeile verzichten. Aber wenn man sie entfernt oder auskommentiert, meldet BlueJ den Fehler, dass die return-Anweisung fehlt. Also bleibt die untere return-Anweisung hier stehen.
Die Methode analyse() bestimmt zuerst die Suchzeit für 10 Zufallszahlen in dem unsortierten Array. Dann wird der Array sortiert und nun wird die Suchzeit für die gleichen 10 Zufallszahlen in dem sortierten Array ermittelt. Beim ersten Durchgang wird auf konventionelle Weise nur von links gesucht.
Beim nächsten Durchgang wird das optimierte Verfahren angewendet. Bei Zahlen < 50 wird von links gesucht, bei Suchzahlen >= 50 von rechts:
sum = 0;
for (int n=0; n < 10; n++)
{
if (suchzahl[n] <= 50)
sum = sum + suchzeitVonLinksSortiert(suchzahl[n]);
else
sum = sum + suchzeitVonRechtsSortiert(suchzahl[n]);
}
Damit immer wieder die gleichen Suchzahlen verwendet werden können, wurden diese in einem zweiten kleinen Array gespeichert:
for (int i=0; i < 10; i++)
suchzahl[i] = wuerfel.nextInt(100)+1;
Hier nun die Ergebnisse einiger Durchläufe:
Suchzeit für 10 Zahlen im unsortierten Array: 188 Suchzeit für 10 Zahlen im sortieren Array, von links: 125 Suchzeit für 10 Zahlen im sortieren Array, von links oder rechts: 38
Und hier ein zweiter Durchlauf des Programms:
Suchzeit für 10 Zahlen im unsortierten Array: 168 Suchzeit für 10 Zahlen im sortieren Array, von links: 91 Suchzeit für 10 Zahlen im sortieren Array, von links oder rechts: 58
Das Testprogramm bestätigt also auf eindrucksvolle Weise, dass
a) das Suchen in einem sortierten Array schneller ist als in einem unsortierten,
b) die optimierte Suche (von links und rechts) noch bessere Ergebnisse liefert.
Suchverfahren
Das Thema "Suchverfahren" ist fast genau so wichtig in der Informatik wie das Thema "Sortierverfahren". In der Stufe Q1 werden wir dieses Thema noch etwas vertiefen. Dann werden wir auch binäre Suchverfahren und andere verbesserte Strategien kennenlernen.
Seitenanfang -
Weiter mit der Klasse "Liste" …