Ein sehr schön gemachtes und anschauliches Video zum Selectionsort, in dem auch auf das Zeitverhalten des Algorithmus eingegangen wird. Unbedingt anschauen!
Allgemeines
Der Selectionsort ("Sortieren durch Auswählen") ist ähnlich wie der Bubblesort ein einfaches Sortierverfahren.
Für den Selectionsort teilen wir das Array gedanklich in zwei Teile:
- Bereits sortierter Teil
- Noch unsortierter Teil
Im folgenden Bild ist der sortierte Teil rot, der unsortierte Teil grün markiert.
Im ersten Sortierschritt wird die kleinste Zahl im unsortierten Teil gesucht (im Bild gelb markiert) und mit der ersten Zahl des unsortierten Teils vertauscht:
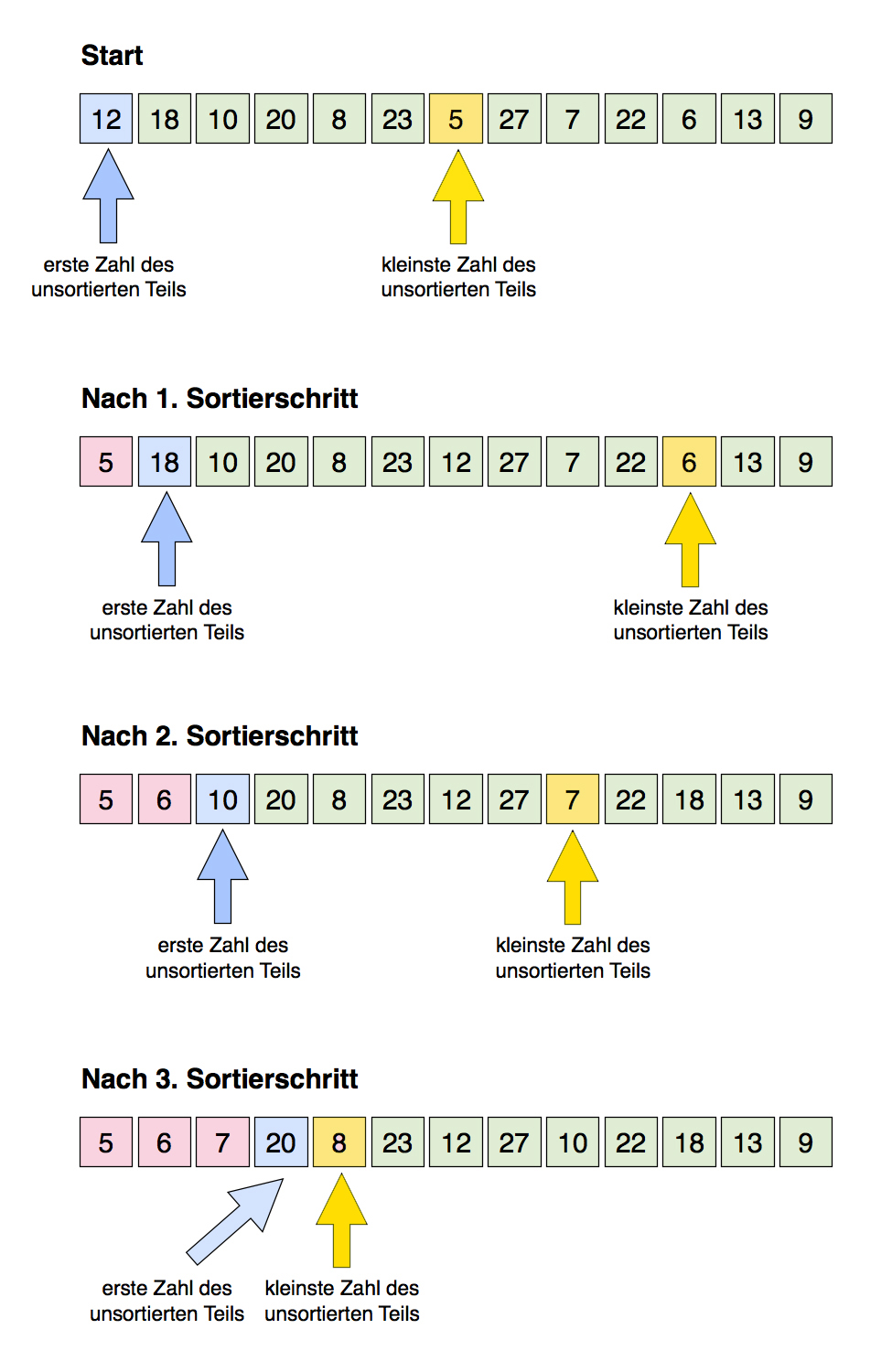
Die ersten drei Sortierschritte des Selectionsort
Autor: Ulrich Helmich, Lizenz: Public domain
Hier sehen wir die ersten drei Sortierschritte des Selectionsort. Danach besteht der sortierte Teil aus drei Elementen.
Die Implementierung dieses Algorithmus in Java ist recht einfach:
public void selectionsort()
{
for (int i=0; i < zahl.length; i++)
tausche(i,getMiniPos(i));
}
Die Methode getMiniPos() sucht den Index der kleinsten Zahl im unsortierten Teil des Arrays, der hier als Instanzvariable zahl vorliegt. Der Anfangsindex des unsortierten Teil muss der Methode als Parameter übergeben werden (hier: start), damit die Suche nur im unsortierten Teil stattfindet.
Übungen
Übung 5.3-1
- Erweitern Sie das Java-Projekt aus dem Bubblesort-Abschnitt um eine sondierende Methode
private int getMiniPos(int start)
die den Index der kleinsten Zahl des unsortierten Teils des Arrays zurück liefert.
Angenommen, das Array besteht aus den Zahlen 1 - 2 - 7 - 4 - 6 - 3.
Der sortierte Teil besteht aus den beiden ersten Zahlen, der unsortierte Teil beginnt mit der Zahl 7. Dann würde getMiniPos(2) den Wert 5 liefern, denn die kleinste Zahl 3 befindet sich an Index 5 des Arrays. - Schreiben Sie eine Methode tausche(int i, int j), welche die beiden Zahlen an den Indices i und j miteinander vertauscht.
- Testen Sie dann mit Hilfe der oben dargestellten Methode selectionsort(), ob Ihre getMiniPos()- und tausche()-Methoden funktionieren.
Interessant ist nun die Frage, ob der Selectionsort schneller abläuft als der Bubblesort. Eigentlich ist das gar keine Frage, da man in jedem Informatikbuch lesen kann, dass der Bubblesort eines der langsamsten Sortierverfahren ist. Die eigentliche Frage ist: Wie viel mal schneller ist der Selectionsort, um welchen Faktor wird das Sortieren von 100, 1.000 oder 10.000 Zahlen beschleunigt?
Übung 5.3-2
Vergleichen Sie die Geschwindigkeit des Bubblesorts mit der des Selectionsorts. Verwenden Sie dabei eine Methode zur Messung der Systemzeit oder ergänzen Sie die Quelltexte der drei Methoden getMiniPos(), tausche() und selectionsort() um eine Zählvariable, die die Vergleichs- und Tauschvorgänge während des Ablaufs des Algorithmus mitzählt.
Vergleichen Sie dann die Sortierzeiten bzw. die Zahl der Operationen von Bubblesort und Selectionsort für 100, 200, 400, 800 und 1600 Zahlen, wenn Sie mit einer Zählvariable arbeiten, bzw. für 10.000, 20.000, 40.000 und 80.000 Zahlen, wenn Sie mit der Systemzeit arbeiten.
Übung 5.3-3 für Experten
Es ist doch recht umständlich, wenn man die Anzahl der sortierenden Arrayelemente jedes Mal vor dem Kompilieren von Hand ändern muss. Überlegen Sie, wie man das automatisieren könnte.
Erweitern Sie die Klasse, die die beiden Sortieralgorithmen enthält, so dass bubblesort() und selectionsort() nacheinander für eine Reihe festgelegter Arraylängen (vgl. Übung 2) ausgeführt werden. Die jeweils ermittelten Messwerte sollen anschließend strukturiert und gut lesbar in der Konsole ausgegeben werden.
Aufgabe 5.3-4
Bei meinen eigenen Experimenten habe ich festgestellt, dass der Selectionsort deutlich schneller ausgeführt wird als der Bubblesort, obwohl doch beide Algorithmen ein ähnliches Zeitverhalten O(N2) haben.
Für 100 Zahlen benötigte der Bubblesort bei mir 37.399 Operationen (Vergleiche und Zuweisungen), während der Selectionsort nur 16.415 Operationen benötigte, also deutlich weniger als die Hälfte. Diese Messungen bestätigen die oft zitierte Behauptung, dass der Bubblesort der langsamste der einfachen Sortieralgorithmen ist.
| MAX | Bubblesort | Selectionsort |
| 100 | 37.399 | 16.415 |
| 200 | 148.615 | 62.987 |
| 400 | 595.222 | 246.677 |
| 800 | 2.385.640 | 974.291 |
| 1600 | 9.600.076 | 3.871.203 |
Finden Sie eine logische Begründung für dieses unterschiedliche Zeitverhalten von Bubble- und Selectionsort.
Seitenanfang
Weiter mit dem Insertionsort ...