Zielsetzung
Ziel dieses Abschnitts ist es nicht, einen Algorithmus für das Einfügen eines neuen Elements in einen ausgeglichenen Baum zu entwickeln. Die von WIRTH und anderen Autoren entwickelten Algorithmen mit ihren Links-, Rechts-, doppelten LR-Rotationen und wie sie alle heißen sind für einen Informatik-Grundkurs sicherlich zu "hoch", auch für einen Informatik-LK. Aber zumindest die Grundideen wollen wir hier nachvollziehen.
Betrachten wir folgenden bereits ausgeglichenen binären Suchbaum:
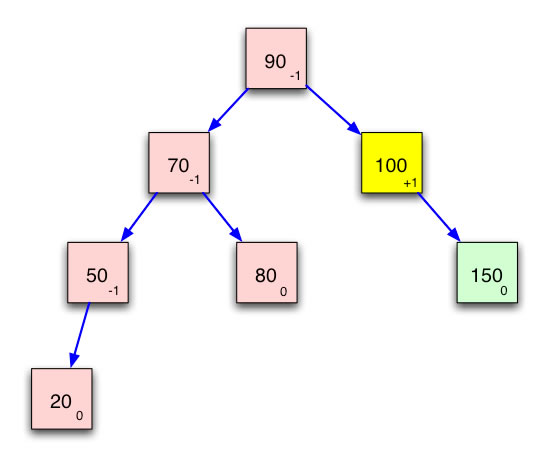
Ein ausgeglichener binärer Suchbaum
Wir wollen nun die Zahl 85 in den Suchbaum einfügen. Das sollte überhaupt kein Problem sein, denn durch das Anhängen der 85 rechts an die 80 bleibt die 80 ausgeglichen (+1), während die 70 ihre Bilanz sogar noch verbessert (0). Die 90 bleibt ebenfalls in ihrer Bilanz unverändert (-1). Die erste Frage, die ein Insert-Algorithmus also klären muss, ist die, ob durch das Einfügen die Bilanz eines Knotens derart verändert wird, dass dieser Knoten (und damit der ganze Baum) nicht mehr ausgeglichen ist. Wenn wir die Zahl 10 in den Baum einfügen, haben wir einen solchen Fall:
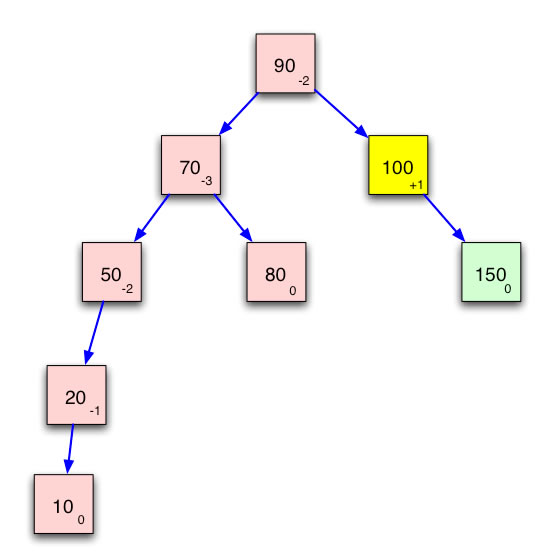
Der Baum wird durch das Einfügen der 10 linkslastig
Es ist offensichtlich, was der Algorithmus nun machen muss. Die Knoten im linken Unterbaum (mit der 70 als Wurzel) müssen "verschoben" werden, so dass der linke Unterbaum ausgeglichen ist. Eine mögliche Lösung könnte so aussehen:
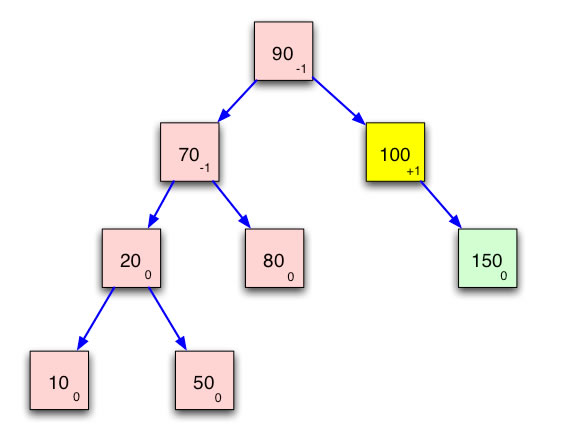
Der Baum ist wieder ausgeglichen
Die drei Elemente 50, 20 und 10 wurden gewissermaßen rechts herum rotiert, man könnte dies also als Rechts-Rotation bezeichnen. Auf das "Zeigerumbiegen", welches diese Rechtsrotation ermöglicht, wollen wir hier nicht weiter eingehen.
Vorteile von ausgeglichenen Bäumen
Schauen Sie sich die folgenden Bäume an; links nicht ausgeglichen, rechts ausgeglichen:
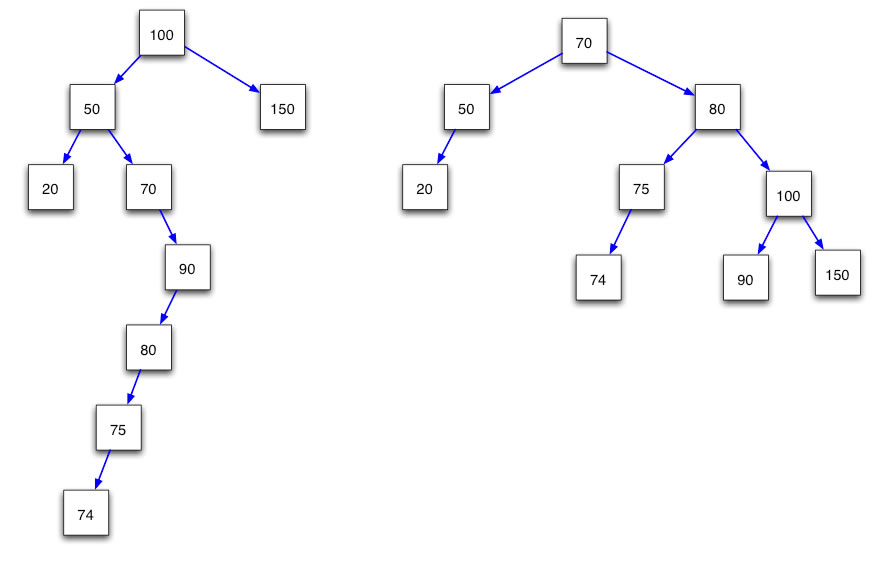
Ein Baum - zwei Versionen
Aufgabe:
Berechnen Sie die durchschnittliche Suchzeit für vorhandene Zahlen in den beiden Bäumen!
Lösung:
Im Grunde muss man hier gar nicht rechnen, man "sieht" die Lösung schon. Das Suchen in dem rechten Baum geht viel schneller als in dem linken Baum, weil der rechte Baum ausgeglichen ist.
Bereits dieses einfache Beispiel zeigt, dass das Suchen in einem ausgeglichenen Baum durchaus schneller geht als in einem nicht ausgeglichenen Baum. Zeit kostet Geld, sagt man, und bei wirklich großen Datenbanken macht sich dieser Unterschied schon bemerkbar.
Übertroffen werden ausgeglichene Bäume nur noch durch völlig ausgeglichene Bäume, bei denen jede Ebene mit der maximalen Zahl von Knoten besetzt ist, was bei einem ausgeglichenen Baum ja nicht der Fall sein muss. Die Konstruktion eines solchen völlig ausgeglichenen Baumes ist jedoch sehr aufwändig und lohnt sich eigentlich nur dann, wenn die Häufigkeit des Suchens sehr viel größer ist als die Häufigkeit des Einfügens neuer Elemente.
Zwei russische Mathematiker, nämlich Georgi Maximowitsch ADELSON-VELSKI und Jewgeni Michailowitsch LANDIS, haben sich in den 60er Jahren des letzten Jahrhunderts sehr intensiv mit ausgeglichenen Bäumen beschäftigt. Sie haben z.B. berechnet, dass ein ausgeglichener Baum maximal 45% höher ist (mehr Ebenen hat) als ein völlig ausgeglichener Baum. Nach den Namen dieser beiden Forschern werden ausgeglichene Bäume häufig als AVL-Bäume bezeichnet.