27.2 Eindeutige Grammatiken

Eindeutige Grammatiken

Was eine kontextfreie Grammatik ist, haben Sie hoffentlich verstanden. Nämlich eine Grammatik, bei der alle Produktionsregeln die Form

A ---> a*

haben, mit A = Nichtterminal und a* = eine Folge von Terminalen und/oder Nichtterminalen. Auf der linken Seite der Produktionsregeln steht also immer ein einziges Nichtterminal.

Was ist nun eine eindeutige Grammatik? Betrachten wir zunächst eine Grammatik, die nicht eindeutig ist, dann verstehen Sie das Ganze besser. Wenn man eine Grammatik beschreibt, reicht es meistens aus, wenn man nur die Produktionsregeln angibt. Die Mengen N und T sowie das Startsymbol können dann diesen Regeln entnommen werden. Aber bitte nicht im Informatik-Abitur! Hier wird immer verlangt, die komplette Grammatik anzugeben, also das 4-Tupel mit den zugehörigen Erklärungen.

P1: Expr ---> Expr + Expr
P2: Expr ---> Expr * Expr
P3: Expr ---> num
P4  Expr ---> ( Expr )

Die Grammatik ist also sehr einfach und umfasst nur vier Produktionsregeln. Aber wieso ist diese Grammatik nicht eindeutig?

Schauen wir uns die Herleitung des Ausdrucks num + num * num näher an.

Expr              ===1===> Expr + Expr
Expr + Expr       ===3===> num + Expr
num + Expr        ===2===> num + Expr * Expr
num + Expr * Expr ===3===> num + num * Expr
num + num * Expr  ===3===> num + num * num

Wir haben also folgende Regeln in folgender Reihenfolge angewandt: 1, 3, 2, 3, 3.

Da immer das am weitesten links stehende Nichtterminal erweitert wird, reicht es im Grunde aus, nur die Nummern der angewandten Produktionen anzugeben, um einen Ausdruck aus dem Startsymbol herzuleiten.

Betrachten wir nun eine andere Ableitung:

Expr               ===2===> Expr * Expr
Expr * Expr        ===1===> Expr + Expr * Expr
Expr + Expr * Expr ===3===> num + Expr * Expr
num + Expr * Expr  ===3===> num + num * Expr
num + num * Expr   ===3===> num + num * num

Wir haben also die Ableitung 2, 1, 3, 3, 3 durchgeführt.

Mit anderen Worten: Es gibt zwei völlig verschiedene Wege, den String num + num * num aus dem Startsymbol herzuleiten. Eine solche Grammatik ist nicht eindeutig!

Für theoretische Betrachtungen ist es recht unerheblich, ob eine Grammatik eindeutig oder nicht eindeutig ist. Will man dagegen einen Parser konstruieren, der Syntaxanalyse betreiben kann, so muss die Grammatik zwingend eindeutig sein. Wenn der Parser einen Tokenstrom wie

num + num * num

vom Lexer bekommt, so muss der Parser diesen Tokenstrom auf das Startsymbol der Grammatik zurückführen. Dabei muss der Parser bestimmte Entscheidungen treffen. Damit er nicht "hängen bleibt", muss die Grammatik eindeutig sein; es darf nur ein Weg vom Tokenstrom zum Startsymbol existieren.

Parsebäume

Eine Ableitung, d.h. die Herleitung eines ausschließlich aus Terminalzeichen bestehenden Strings aus dem Startsymbol einer Grammatik, kann man auch graphisch in Form eines Parsebaums darstellen. Die folgende Zeichnung zeigt einen solchen Parsebaum für eine andere, komplexere Grammatik mit mehr als einem Nichtterminal, nämlich N = {Expr, Term, Fact} und Expr als Startsymbol:

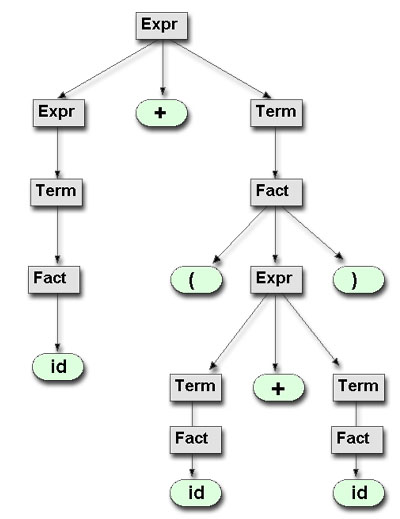
Ein Parsebaum für einen artihmetischen Ausdruck

Die Wurzel des Baumes ist identisch mit dem Startsymbol der Grammatik. Die Blätter des Baumes (grün gezeichnet) sind identisch mit den Terminalsymbolen des abgeleiteten Ausdrucks. Die Blätter müssen - ähnlich wie bei einem binären Suchbaum - von links nach rechts gelesen werden. Für den hier gezeigten Baum erhält man dann den Terminalstring

id + ( id + id )

Aus der Sicht des Parsers gesehen ist ein Parsebaum der Weg, wie man von einem Terminalstring (den Blättern) zurück zum Startsymbol (der Wurzel) gelangen kann.

Den Begriff "Eindeutige Grammatik" kann man jetzt neu definieren:

Wenn man jetzt einen konkreten Parser für eine Sprache programmieren möchte, so muss man darauf achten, dass die zu Grunde liegende Grammatik eindeutig ist. Nur dann weiß der Parser bei jedem Reduktionsschritt genau, wie er sich verhalten soll. Bei einer mehrdeutigen Grammatik (mit mehreren Parsebäumen für einen Ausdruck) gibt es Stellen im Reduktionsprozess, an denen der Parser nicht weiß, was er machen soll.

Ein Beispiel für eine eindeutige Grammatik

P1: Expr --> Term 
P2: Expr --> Expr + Term
P3: Expr --> Expr - Term

P4: Term --> Fact 
P5: Term --> Term * Fact
P6: Term --> Term / Fact

P7: Fact --> num
P8: Fact --> id
P9: Fact --> (Expr)

Hier sehen Sie eine eindeutige Grammatik für arithmetische Ausdrücke mit Zahlen (num) und Variablen (id). Allerdings habe ich mir diese Grammatik nicht selbst ausgedacht, sie stammt aus dem berühmten "Drachenbuch" Compilerbau, Teil 1 von Aho, Sethi und Ullman, das  leider nur in einer alten Auflage von 1999 existiert.

Ein Beispiel für eine Syntaxanalyse

Betrachten wir noch einmal obige Grammatik mit den neun Produktionsregeln P1 bis P9 und den vereinfachten Tokenstrom

(num + num) * num

Wir wollen diesen Ausdruck nun durch Rückwärtsableitungen auf das Startsymbol Expr reduzieren.

1. Schritt

Wir suchen uns eine Produktionsregel aus, auf deren rechter Seite ein Ausdruck steht, der in dem vereinfachten Tokenstrom vorkommt. Dabei fällt uns als erstes die Regel 7 ins Auge, hier steht auf der rechten Seite nämlich nur das Terminalsymbol num. Durch Rückwärts-Anwendung von P7 erhalten wir:

(num + num) * num <--- (Fact + num) * num

2. Schritt

Da wir die Reduktion auf das Startsymbol Expr im Auge haben, wenden wir auf das Nichtterminal Fact nun die Regel 4 an und erhalten

(Fact + num) * num <--- (Term + num) * num

3. Schritt

Jetzt wenden wir die Regel 1 auf das Nichtterminal Term an und erhalten

(Term + num) * num <--- (Expr + num) * num

4. Schritt

Wir beschäftigen uns nun mit dem am weitesten links stehenden num, durch Anwendung der Regel 7 erhalten wir

(Expr + num) * num <--- (Expr + Fact) * num

5. Schritt

Mit der Regel 4 erhalten wir

(Expr + Fact) * num <--- (Expr + Term) * num

6. Schritt

Mit Regel 2 kann man Expr + Term auf Expr reduzieren:

(Expr + Term) * num <--- (Expr) * num

7. Schritt

Mit Regel 9 erhalten wir aus (Expr) das vereinfachte Fact:

(Expr) * num <--- Fact * num

8. Schritt

Mit Regel 4 erhalten wir

Fact * num <--- Term * num

9. Schritt

Der Parser muss jetzt eine Art Eigenintelligenz entwickeln. Denn theoretisch könnte er jetzt auf das Nichtterminal Term die Regel 1 anwenden und

Expr * num

herleiten. Dies wäre aber fatal, denn es gibt keine Produktionsregel, auf deren rechter Seite der Ausdruck Expr * num, Expr * Fact oder Expr * Expr vorkommt. Dagegen gibt es die Regel 5 mit der rechten Seite Term * Fact. Daher macht der Parser an dieser Stelle Schluss mit der Reduktion des Nichtterminals und wendet sich dem noch verbliebenen Terminal num zu. Durch Anwendung der Regel 7 erhalten wir zunächst

Term * num <--- Term * Fact

10. Schritt

Diesen Ausdruck kann der Parser durch Anwendung der Regel 5 auf Term reduzieren:

Term * Fact <--- Term

11. Schritt

Jetzt kann Regel 1 angewandt werden, und der Parser erhält schließlich

Term <--- Expr

das Startsymbol der Grammatik.

Damit wäre der Ausdruck

(num + num) * num

erfolgreich auf das Startsymbol der Grammatik reduziert worden. Der Ausdruck gehört somit zur Sprache L(G).