Ein sehr schön gemachtes und anschauliches Video zum Mergesort, in dem auch auf das Zeitverhalten des Algorithmus eingegangen wird. Unbedingt anschauen!
5.6.1 Vorbereitung des Mergesorts
Der Mergesort gehört nicht mehr zu den einfachen Sortierverfahren, sondern zu den komplexeren, lässt sich aber relativ einfach verstehen.
Betrachten wir noch einmal den Bubblesort, eines der einfachen Sortierverfahren. Wir versuchen nun einmal, den Bubblesort zu optimieren.
Grundidee
Der Bubblesort hat ein quadratisches Zeitverhalten. Stellen wir uns vor, dass wie zum Sortieren von 10 Zahlen 100 Zeiteinheiten benötigen. Dann brauchen wir für das Sortieren von 20 Zahlen 400 Zeiteinheiten, für 30 Zahlen 900 und für 40 Zahlen sogar 1.600 Zeiteinheiten.
Wir teilen die 40 zu sortierenden Zahlen nun in zwei Hälften auf und sortieren jede Hälfte für sich. Dann benötigen wir 2 x 400 = 800 Zeiteinheiten sowie noch mal 20 Zeiteinheiten für das Verschmelzen der beiden sortierten Arrayhälften. Diese paar Zeiteinheiten können wir nahezu vernachlässigen. Daher können wir sagen, dass dieser 2fach-Bubblesort statt 1.600 Zeiteinheiten nur 800 Zeiteinheiten kostet.
Verschmelzen von zwei sortierten Arrays
Und schon sind wir bei einem zentralen Punkt des Mergesort-Verfahrens. Das Wort "merge" heißt nämlich so viel wie "Verschmelzen" oder "Vereinigen". Schauen wir uns einen einfachen Java-Algorithmus an, mit dem man zwei bereits sortierte Arrays zu einem neuen sortierten Array verschmelzen ("mergen") kann:
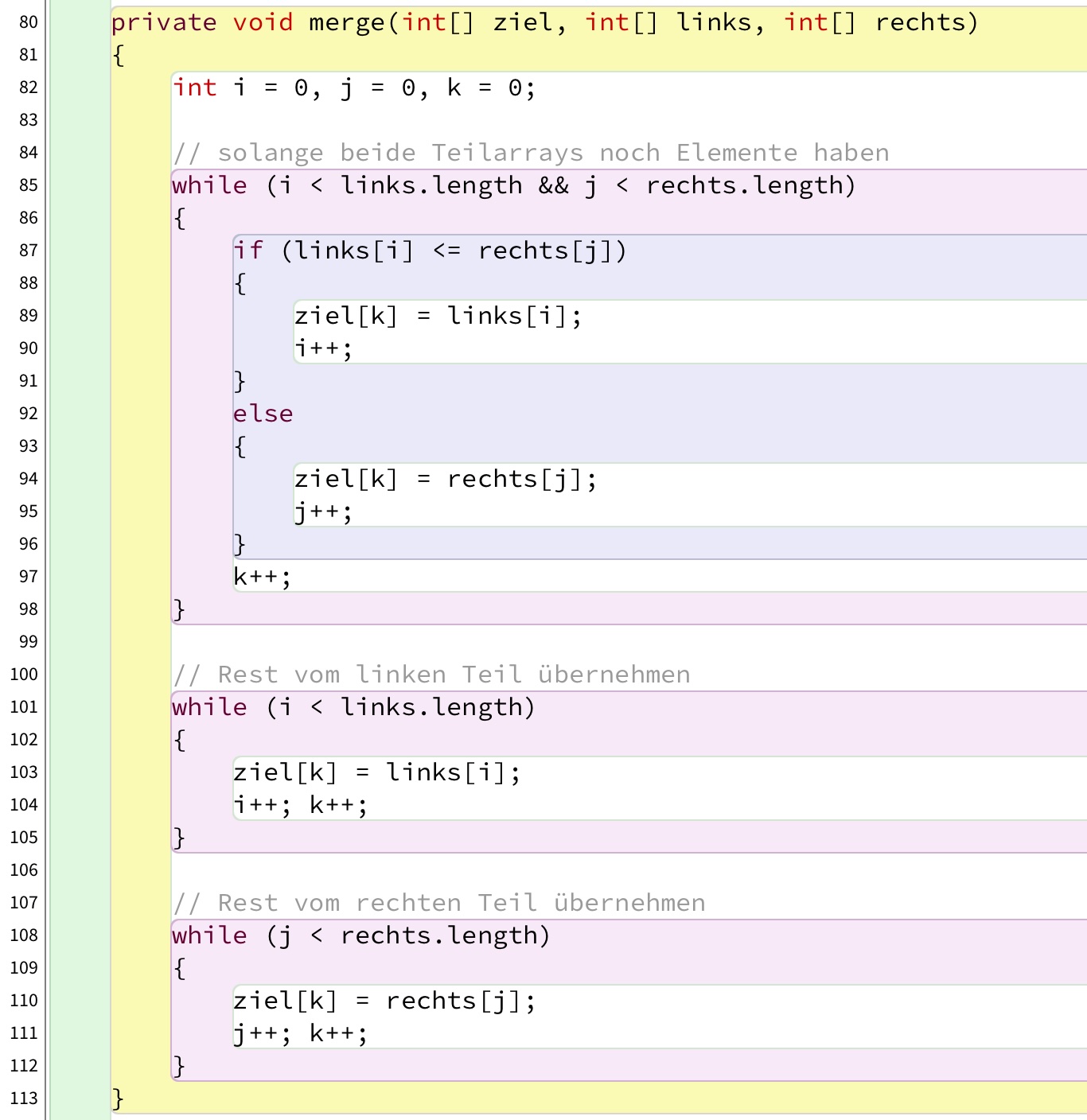
Die Methode merge()
Diese Methode hat drei Parameter vom Typ int[], nämlich links, rechts und ziel. Die beiden Arrays links und rechts sind die beiden Teilarrays, die zum Array ziel vereinigt werden sollen.
Schauen wir uns diesen Merge-Prozess einmal näher an.
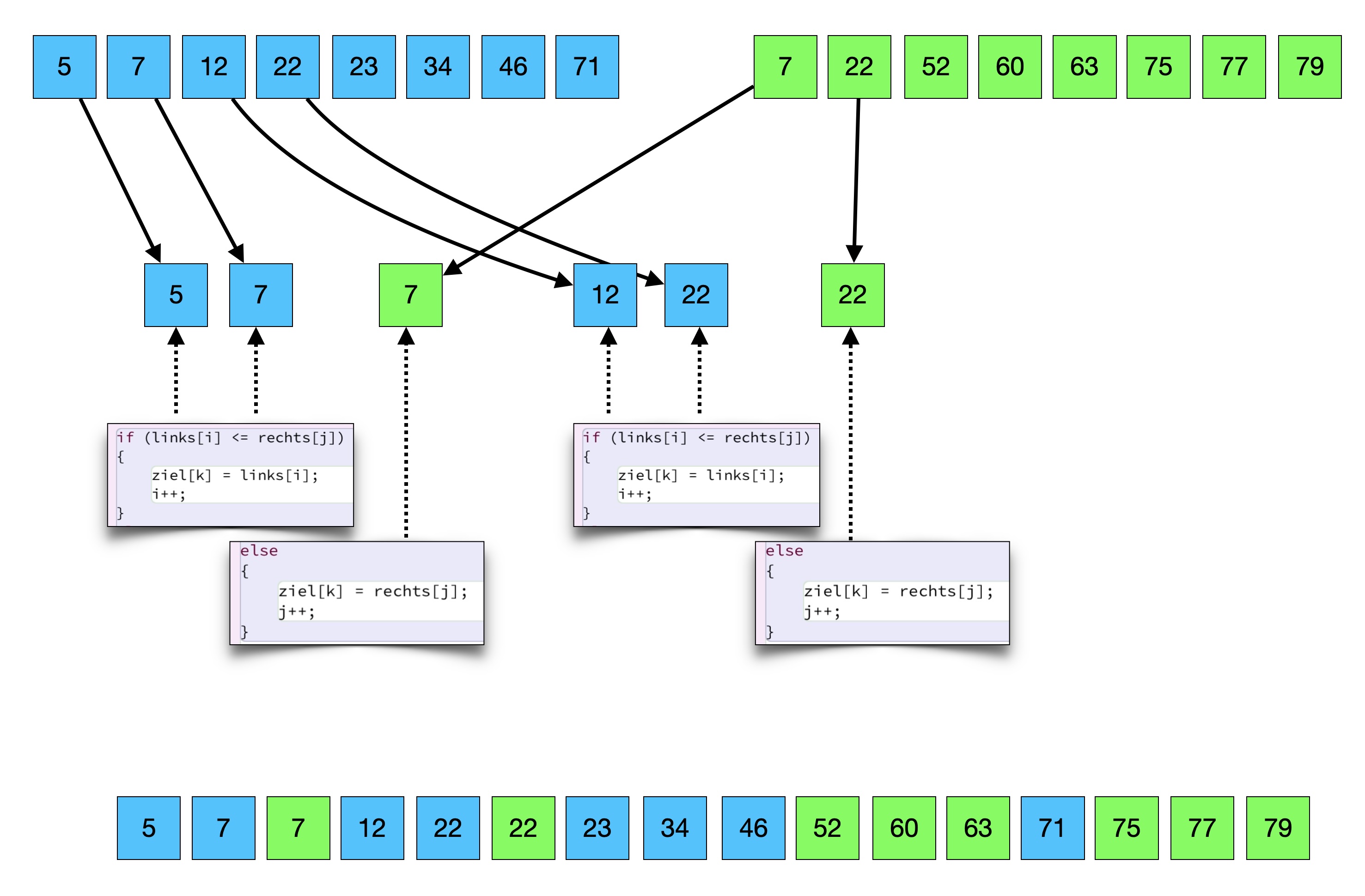
Die ersten Schritte der Methode merge()
(C) Ulrich Helmich 2025, Public domain.
In der ersten while-Schleife werden zunächst die Zahlen des linken Arrays untersucht (hier blau markiert). Immer dann, wenn eine Zahl nicht größer (also <=) ist als die nächste Zahl im rechten Array, wird die linke Zahl in den Ziel-Array übertragen. Sollte die Bedingung (links[i] <= rechts[j]) nicht erfüllt sein, wird die nächste Zahl des rechten Arrays (grün markiert) in den Zielarray eingebaut.
Die beiden while-Schleifen am Ende des Quelltextes sind für den Fall gedacht, dass der eine Array schon vollständig im Zielarray untergebracht wurde. Dann werden die letzten Zahlen des anderen Arrays einfach an das Ende des Zielarrays kopiert. In unserem Beispiel ist das der Fall, wenn der Zähler i bei dem Arrayelement 71 des linken Arrays angekommen ist. Dann können die drei letzten Elemente des rechten Arrays einfach in den Zielarray übernommen werden, ohne dass vorher noch eine Überprüfung stattfinden muss.
Schauen Sie sich nun den folgenden Quelltext an:
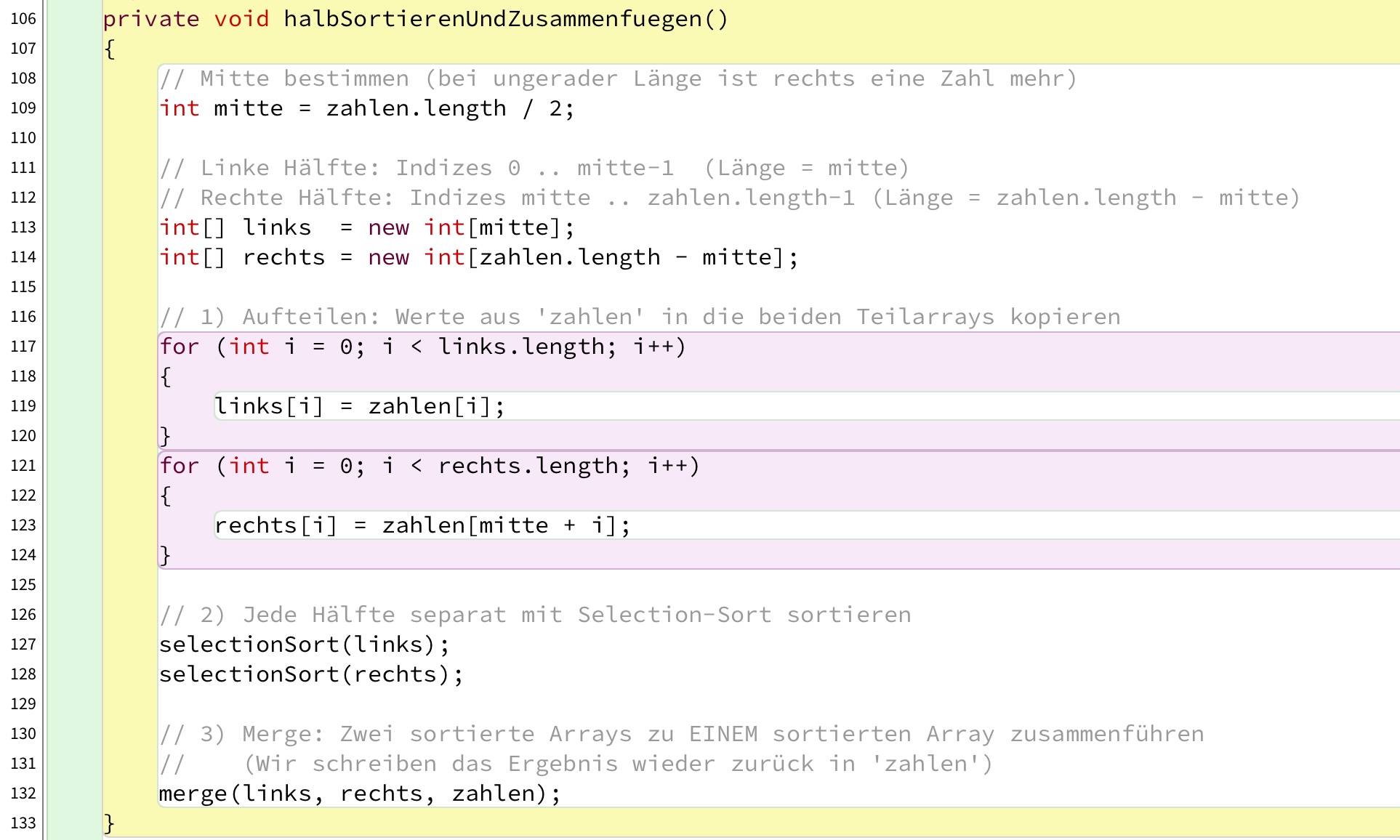
Eine Methode, die zwei Halb-Arrays sortiert und dann zusammenfügt
Hier sehen wir eine aufwendig kommentierte Methode halbSortierenUndZusammenfuegen().
In der Zeile 109 wird die Mitte des Arrays bestimmt: mitte = zahlen.length/2.
Dann werden zwei Hilfs-Arrays links und rechts angelegt (Zeilen 113, 114), und in den Zeilen 117 bis 124 wird erst die linke Hälfte, dann die rechte Hälfte des Original-Arrays in die beiden Hilfs-Arrays kopiert.
In den Zeilen 127, 128 wird jedes Hilfs-Array nicht mit einem Bubblesort, sondern mit einem Selectionsort aufsteigend sortiert.
In der Zeile 132 schließlich werden die beiden Hilfs-Arrays mit der bereits oben besprochenen merge()-Methode zum Ziel-Array zahlen zusammengefügt.
Zeitverhalten (mit KI-Hilfe)
Das Programm zum zweifachen Selectionsort wurde dann mit KI-Hilfe (ChatGPT) etwas "aufgebohrt", indem das Zeitverhalten des normalen Selectionsort und des hier optimierten Selection/Merge-Sorts gemessen wurde. Hier die Ergebnisse:
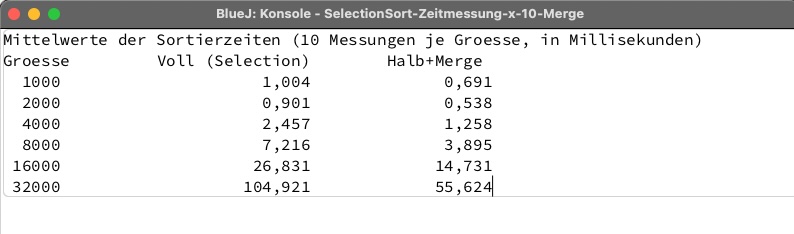
Zeitverhalten
Es wurde die Sortierzeit in ms für 1000, 2000, 4000, 8000, 16000 und 32000 Zahlen auf einem MacStudio mit M1-Max-Prozessor gemessen, und zwar über die Methode System.nanoTime(), welche die Zeit in Nanosekunden zurückliefert.
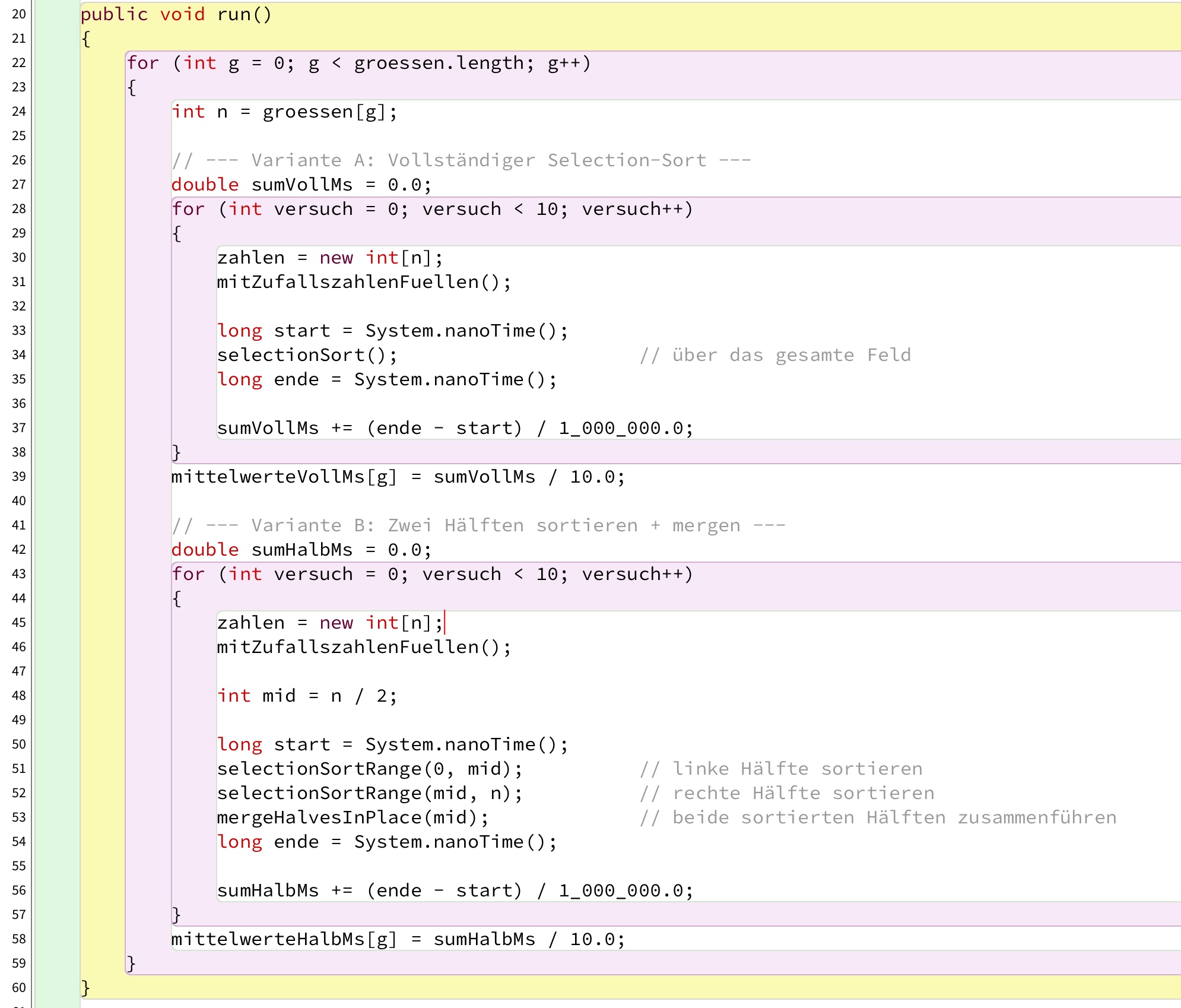
Die entscheidende Mess-Methode
Hier sehen wir die entscheidende Mess-Methode. Die Array-Größen 1000, 2000, 4000, 8000, 16000 und 32000 sind in einem eigenen Hilfs-Array groessen gespeichert. In der Zeile 24 wird die jeweilige Größe ausgelesen und in der Variable n gespeichert.
In den Zeilen 26 bis 39 wird das Zeitverhalten des normalen Selectionsort ermittelt. Für jede Array-Größe werden 10 Versuche durchgeführt. Für jeden der 10 Versuche wird ein neues Array zahlen angelegt (Zeile 30) und mit Zufallszahlen gefüllt (Zeile 31). Dann wird die Systemzeit ausgelesen (33), der Selectionsort durchgeführt (34) und dann die neue Systemzeit gelesen (35). In Zeile 37 wird die Zeitdifferenz in Nanosekunden berechnet und dann durch 1.000.000 dividiert, um die Zeitdifferenz in Millisekunden ausgeben zu können.
Ab Zeile 42 wird dann der optimierte Selectionsort durchgeführt. Dazu wurde die Methode selectionSort() etwas modifiziert, so dass sie nicht das gesamte Array sortiert, sondern nur die linke oder rechte Hälfte. In Zeile 48 wird die Mitte des Arrays ermittelt. Dann wird wieder die Zeit festgehalten (50), anschließend wird die linke Hälfte sortiert, dann die rechte (51,52) und schließlich wird eine merge()-Methode ausgeführt, welche die beiden sortierten Hälften wieder zusammenführt (53).
ChatGPT hat die von mir entwickelte merge()-Methode etwas vereinfacht, so dass nicht mehr drei Array-Parameter übergeben werden müssen. Auch die Idee, die Zeiten mit System.nanoTime() auszulesen, kam von ChatGPT. Ich hätte ansonsten System.currentTimeMillis() verwendet.
Wenn wir und jetzt die Ergebnisse der Zeitmessung anschauen, sehen wir sofort, dass sich das Aufteilen, getrennte Sortieren und Wiedervereinigen gelohnt hat. Das optimierte Verfahren ist ungefähr doppelt so schnell wie das einfache - genau wie vorhergesagt.
Das war noch kein richtiger Mergesort
Allerdings ist das hier gezeigte Verfahren mit halben Arrays noch kein richtiger Mergesort - aber schon mal eine gute Vorbereitung auf den eigentlichen Algorithmus. Dazu kommen wir jetzt.
5.6.2 Der richtige Mergesort
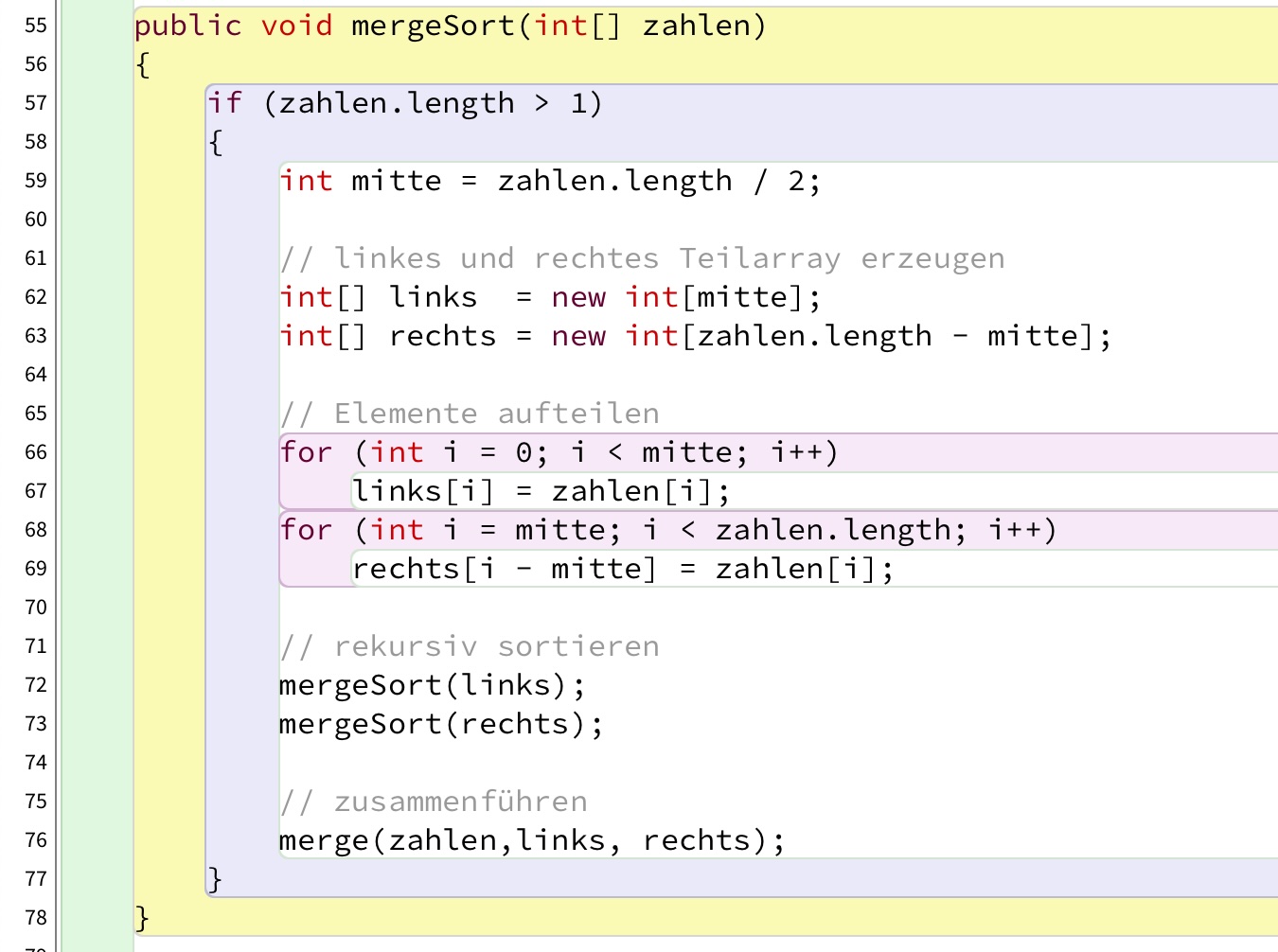
Die mergeSort()-Methode
Hier sehen wir nun endlich die richtigemergeSort()-Methode, wie man sie auch in jedem Fachbuch findet.
In Zeile 59 wird die Mitte des Ausgangs-Arrays bestimmt, dann werden zwei Hilfs-Arrays links und rechts angelegt. Man könnte den Mergesort auch direkt in dem Ausgangs-Array durchgeführen, aber für mich ist das Verfahren mit zwei eigenen Teil-Arrays anschaulicher. Ich habe dann in den Zeilen 66 bis 69 auch ein klassisches Kopierverfahren eingesetzt, man hätte dafür auch einen Spezialbefehle aus der Klasse Array verwenden können.
Dann kommt in den Zeilen 72 und 73 der Clou des Ganzen. Mergesort ruft sich selbst rekursiv auf, einmal für die linke Hälfte, einmal für die rechte Hälfte.
Ausblick, Rekursion
Bevor wir uns nun mit weiteren komplexeren Sortieralgorithmen beschäftigen, sollten wir zunächst tiefer in das Thema "Rekursion" einsteigen.
Seitenanfang
Weiter mit Rekursion ...