Mit Hilfe des Lambert-Beerschen Gesetzes kann man die Konzentration eines Farbstoffs in einem Lösungsmittel berechnen. Die Aussagen dieses Gesetzes, das bereits im Jahre 1729 formuliert wurde, können folgendermaßen vereinfacht zusammengefasst werden:
- Eine Farbstoff-Lösung absorbiert um so mehr Licht, je konzentrierter sie ist.
- Je länger der Weg ist, den das Licht durch die Farbstoff-Lösung zurück legen muss, desto mehr Licht wird absorbiert.
Kommen wir nun zu einer genaueren Darstellung des Lambert-Beerschen Gesetzes:
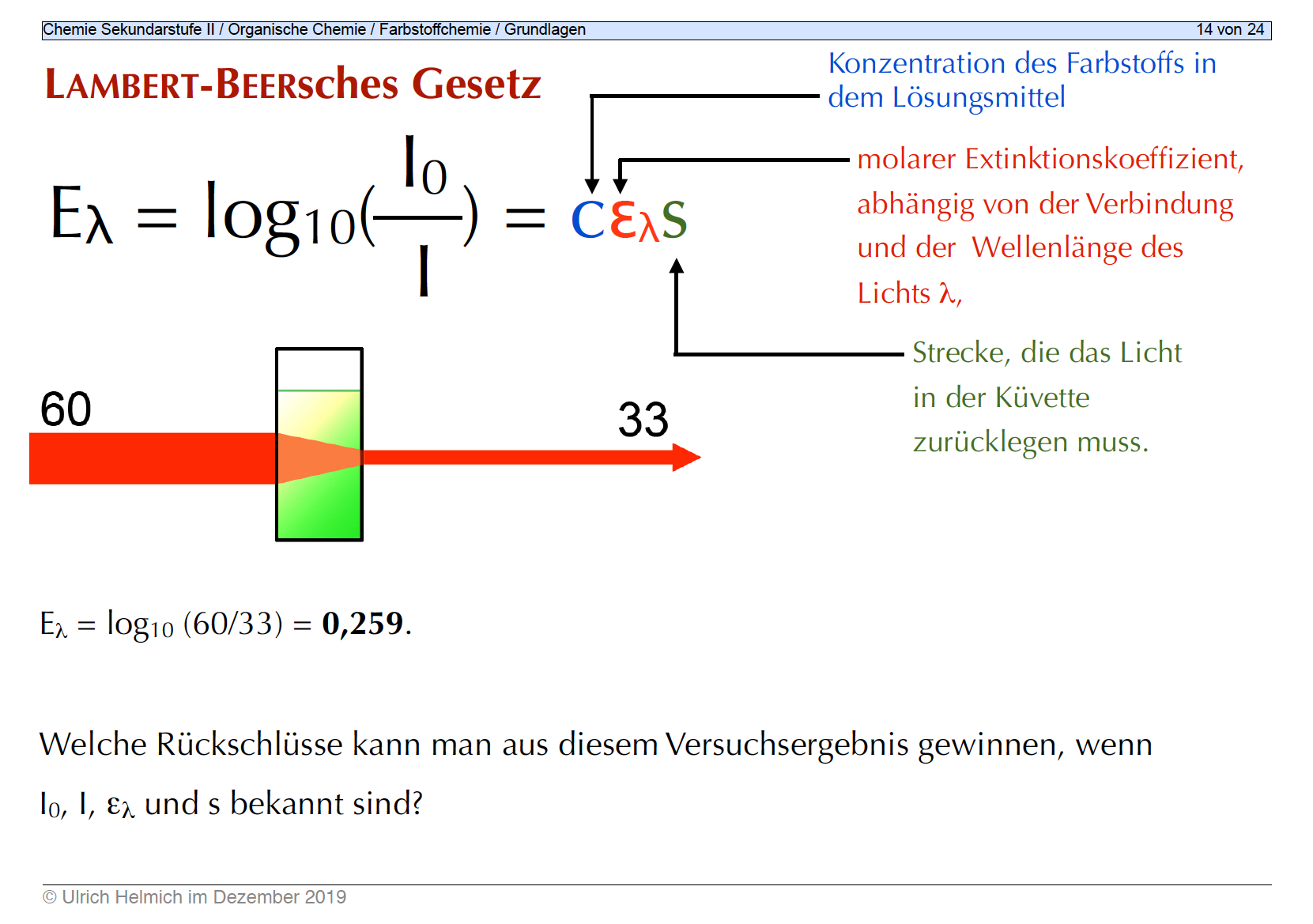
Folie 14 der Präsentation "Grundlagen der Farbstoffchemie"
Autor: Ulrich Helmich 2022, Lizenz: Public domain.
In den meisten Schulbüchern wird dieses Gesetz folgendermaßen formuliert:
$E_{\lambda} = log_{10}(\frac{I_{0}}{I}) = \varepsilon_{\lambda} c s$
Falls der Browser die Formeln auf dieser Seite nicht richtig darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist der Browser veraltet, oder es besteht im Augenblick keine Internetverbindung.
Linke Seite des Gesetzes
Fangen wir mit der linken Seite der Formel an:
$E_{\lambda} = log_{10}(\frac{I_{0}}{I})$
$E_{\lambda}$ ist die sogenannte Extinktion. Unter der Extinktion versteht man ein Maß für die Abschwächung von Licht, nachdem es eine Flüssigkeit durchquert hat. Die Extinktion ist von der Wellenlänge der Strahlung abhängig.
Gemessen wird die Extinktion, indem man die Lichtintensität $I_{0}$ vor dem Durchqueren der Flüssigkeit durch die Lichtintensität $I$ nach dem Durchqueren der Flüssigkeit dividiert und aus dem Quotienten $\frac{I_{0}}{I}$ den dekadischen Logarithmus zieht.
In dem Beispiel, das wir in Abbildung 1 sehen, hatte die Lichtintensität vor dem Durchdringen der Küvette eine relative Intensität von 60 Einheiten. Nach dem Durchdringen der Farbstoff-Lösung in der Küvette konnten aber nur noch 33 Einheiten gemessen werden. Der dekadische Logarithmus aus dem Quotienten (60/33) ist 0,259. Damit hätten wir den Wert für die Extinktion.
Rechte Seite des Gesetzes
Kommen wir nun zur rechten Seite der Formel:
$E_{\lambda} = \varepsilon_{\lambda} c s$
Die rechte Seite besagt folgendes:
- Je größer die Konzentration $c$ des Farbstoffs, desto mehr Licht wird absorbiert.
- Je länger die Wegstrecke $s$, die das Licht in der Lösung zurücklegen muss, desto mehr Licht wird absorbiert.
Der Extinktionskoeffizient $ \varepsilon_{\lambda}$ ist dann die Proportionalitätskonstante.
Anwendung des Lambert-Beerschen Gesetzes
Den Extinktionskoeffizienten $ \varepsilon_{\lambda}$ des Farbstoffs kann man recherchieren. Er hängt von mehreren Faktoren ab, zum Beispiel vom pH-Wert der Lösung oder von der Art des Lösungsmittels.
Die Wegstrecke $s$, die das Licht zurücklegen muss, kann man messen. Normalerweise ist sie identisch mit der Dicke der verwendeten Küvette.
Wenn man diese beiden Werte hat, kann man den dritten Wert $c$ berechnen, nämlich die Konzentration der Farbstoff-Lösung. Und genau dies ist auch die Hauptanwendung des Gesetzes:
Mit dem Lambert-Beerschen Gesetz kann man die Konzentration einer Farbstoff-Lösung berechnen.
Berechnung der Konzentration eines Farbstoffs
Will man die Konzentration einer Farbstoff-Lösung bestimmen, so geht man folgendermaßen vor:
Zunächst führt man die Messung mit einer Farbstoff-Lösung bekannter Konzentration $c_{ref}$ durch, um einen Referenzwert zu erhalten.
Anschließend wiederholt man die Messung mit dem Lösung, deren Konzentration $c$ man bestimmen will.
Man erhält nun zwei Gleichungen:
$E = \varepsilon_{\lambda} c s$
$E_{ref} = \varepsilon_{\lambda} c_{ref} s$
Nun bildet man die Beziehung
$\frac{E}{E_{ref}} = \frac{\varepsilon_{\lambda} \ c \ s}{\varepsilon_{\lambda} \ c_{ref}\ s}$
Man sieht sofort, dass man hier kürzen kann und erhält dann die vereinfachte Darstellung
$\frac{E}{E_{ref}} = \frac{\ c }{\ c_{ref}}$
Die Schichtdicke und der Extinktionskoeffizient fallen weg, sie werden nicht mehr benötigt, da man vorher eine Referenzmessung mit dem gleichen Lösungsmittel und der gleichen Küvettensorte durchgeführt hat.
Nun löst man diese Gleichung nach c auf:
$c = \frac{E}{E_{ref}} c_{ref}$
So erhält man aus der Referenz-Konzentration und den beiden gemessenen Extinktionen die Konzentration der unbekannten Lösung.
Messung der Reaktionsgeschwindigkeit
Bei vielen chemischen Reaktionen treten Farbveränderungen in der Lösung auf. Lässt man beispielsweise Hexen mit Brom reagieren, dann entfärbt sich die anfangs braune Lösung innerhalb weniger Sekunden. Misst man nun kontinuierlich die Extinktion $E_{\lambda}$ mit einem Photometer, so kann man kontinuierlich und quantitativ die Abnahme der Br2-Konzentration verfolgen.
Man kann also die Geschwindigkeit chemischer Reaktionen exakt verfolgen, bei denen ein Farbstoff als Produkt entsteht oder umgekehrt, bei denen ein farbiges Edukt aufgebraucht wird.
Relevanz für den Chemieunterricht
Thema "Geschwindigkeit chemischer Reaktionen"
Hier kann, wie bereits oben beschrieben, die Veränderung der Konzentration einer Edukts oder Produkts während eines Versuchs kontinuierlich verfolgt werden.
Thema "Farbstoffchemie"
Hier wird das Lambert-Beersche Gesetz behandelt, wenn die Grundprinzipien der Lichtabsorption und der Photometrie erklärt werden.