Entropie

Unter dem Begriff "Entropie" versteht man - einfach gesagt - so etwas wie "Unordnung". Bei natürlichen Vorgängen wie zum Beispiel der Diffusion von Teilchen, dem Wärmeausgleich zwischen zwei Körpern, dem Bergabfließen von Wasser und so weiter kommt es zu einer Zunahme der Entropie. Die Beobachtung vieler solcher Phänomene führte dann zum zweiten Hauptsatz der Thermodynamik, nach der die Entropie des Universums ständig zunimmt.

Statistische Deutung der Entropie

Die folgenden Überlegungen gehen auf die Arbeiten von Ludwig Boltzmann (1844 - 1906) zurück. Betrachten wir dazu folgendes Beispiel:

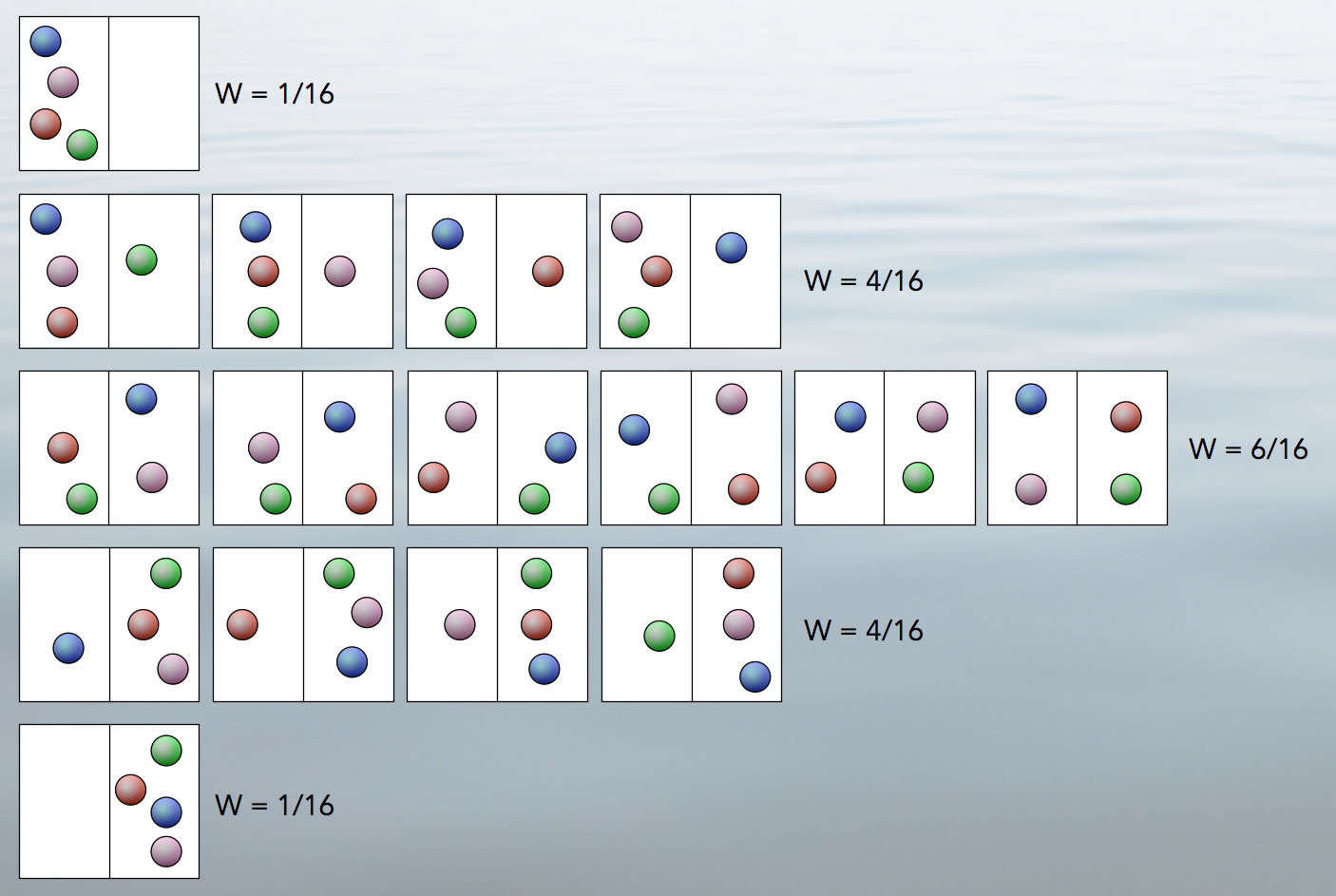
Beispiel für die statistische Deutung der Entropie
Autor: Ulrich Helmich 2022, Lizenz: siehe Seitenende

In einem geschlossenen System, das aus zwei Hälften besteht (links / rechts) befinden sich vier Teilchen. Die Wahrscheinlichkeit, dass sich alle vier Teilchen in der linken Hälfte befinden, ist 1/16, wie man gut nachvollziehen kann, da es insgesamt 16 Möglichkeiten der Verteilung gibt. Für den Makrozustand "3 / 1" gibt es vier Möglichkeiten oder Mikrozustände. Die Wahrscheinlichkeit für diesen Makrozustand ist also 4/16. Der Makrozustand "2 / 2" wird sogar durch sechs Mikrozustände mit einer Wahrscheinlichkeit von 6/16 realisiert, der Makrozustand "1 / 3" durch vier Mikrozustände und der Makrozustand "0 / 4" durch nur einen Mikrozustand.

Nach Boltzmann ist die Entropie eines Makrozustandes nun proportional der Anzahl der Mikrozustände, allerdings wird hier noch eine Logarithmusfunktion "zwischengeschaltet":

S = k_B * ln(Z)

Die Entropie S berechnet sich aus dem natürlichen Logarithmus der Zahl der möglichen Mikrozustände Z eines Systems. k_B ist eine Naturkonstante, die als Boltzmann-Konstante bezeichnet wird. Sie hat einen sehr unanschaulichen Wert von 1,380649 * 10^_-23 J/K, dabei ist K die Maßeinheit Kelvin für die absolute Temperatur. Die Boltzmann-Konstante ist der Quotient aus der allgemeinen Gaskonstanten R und der Avogadro-Konstanten N_A.

Als Entropiezunahme ΔS wird der Entropieunterschied zwischen zwei Makrozuständen bezeichnet.

Betrachten wir das einmal für einen Diffusionsprozess. Am Anfang (Makrozustand 1) befinden sich vier Teilchen in der linken Hälfte eines Gefäßes. Die Entropie dieses Makrozustandes sei S₁ = k_B * ln(Z₁).

Durch die Brownsche Molekularbewegung flitzen die Teilchen in den beiden Hälften des Gefäßes hin- und her. Wie man in der Abbildung 1 gut sehen kann, ist die Wahrscheinlichkeit für den Makrozustand (2 / 2) am größten. In diesem Makrozustand herrscht ein Konzentrationsausgleich. Die Entropie dieses Makrozustandes sei S₂ = k_B * ln(Z₂), dabei gilt S₂ > S₁. Die Differenz S₂ - S₁ kann nun als Entropiezunahme ΔS angesehen werden.

Mathematisch kann man die Entropiezunahme dieses Makrozustand-Wechsels von Z₁ nach Z₂ auch so formulieren:

ΔS = k_B * ln(Z₂/Z₁)

Neben dieser statistischen Interpretation der Entropie gibt es aber auch noch eine chemische, der wir uns nun zuwenden.

Chemische Bedeutung der Entropie

Die Gibbs-Helmholtz-Gleichung

Im Chemieunterricht wird den Schüler(innen) oft das Auflösen von Salzen wie Ammoniumnitrat in Wasser vorgeführt. Zum großen Erstaunen der Schüler(innen) nimmt bei diesem Lösungsvorgang die Temperatur des Wassers ab - ein typisches Beispiel für eine endotherme Reaktion.

Die Frage, die man sich dann im Unterricht stellt, ist die folgende: Wieso läuft diese endotherme Reaktion freiwillig bzw. spontan ab? Normalerweise muss man doch Energie von außen zuführen, damit eine endotherme Reaktion in Gang kommt.

In der Sekundarstufe I müssen sich die Schüler(innen) dann mit der Antwort begnügen, dass die Unordnung beim Auflösen zunimmt, weil aus festen Salzteilchen in Wasser gelöste Ionen werden. Das ist natürlich für den Lehrer gefährlich, weil gute Schüler(innen) dann sofort mit der Frage kommen, wieso sich das Wasser beim Auflösen von Natriumhydroxid erwärmt.

In der Sekundarstufe II kann man dann die Gibbs-Helmholtz-Gleichung einführen und besprechen:

$\Delta G = \Delta H - T \cdot\Delta S $

Beim Auflösen von Ammoniumnitrat nimmt zwar die Enthalpie zu, ΔH>0. Aber die Entropie nimmt ebenfalls zu: ΔS>0.

Multipliziert wird diese Entropiezunahme dann mit der absoluten Temperatur T.

Der Term T * ΔS bekommt ein negatives Vorzeichen, wird also von der Enthalpieveränderung ΔH abgezogen. Ist nun der Term T * ΔS größer als ΔH , dann resultiert ein negatives Ergebnis, es gilt ΔG<0. Eine solche Reaktion wird dann als exergonisch bezeichnet. Exergonische Reaktionen laufen tatsächlich spontan ab.

Mit Hilfe des Entropiebegriffs kann man also recht leicht erklären, wieso manche endotherme Reaktionen trotzdem freiwillig und spontan ablaufen, nämlich immer dann, wenn bei der Reaktion die Entropie stark zunimmt.