Rekapitulation des Kugelwolkenmodells
Aus der Sekundarstufe I oder zumindest aus dem Einführungskurs der Oberstufe sollte Ihnen das Kugelwolkenmodell geläufig sein. Nach diesem Atommodell befinden sich die Elektronen der Atomhülle zwar weiterhin auf diskreten Schalen (K-, L-, M-, N-Schale und so weiter), doch besteht eine solche Schale jetzt aus vier gleichwertigen kugelförmigen Aufenthaltsräumen für je zwei Elektronen, die den Atomkern tetraedrisch umgeben.
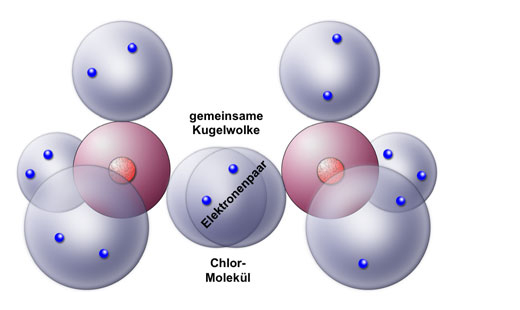
Hier sehen wir zwei Chlor-Atome, dargestellt nach dem Kugelwolkenmodell, die sich zu einem Chlor-Molekül vereinigen, indem die beiden einfach besetzten Kugelwolken der beiden Atome überlappen und so eine gemeinsame Kugelwolke bilden, die von zwei Elektronen besetzt ist. Diese werden dann als Bindungselektronen bezeichnet, und die gemeinsame Kugelwolke könnte man auch als "bindende Kugelwolke" bezeichnen.
Wenn Sie weitere Einzelheiten über das Kugelwolkenmodell erfahren möchte, schauen Sie sich doch bitte die eigentlich für die Klasse 10 geschriebenen Seiten über das Thema " Moleküle" an.
Orbitalmodell, Grundlagen (nach oben)
Am besten erklärt man ein Atommodell, indem man die wichtigsten Atome diesem Modell entsprechend zeichnet und eventuell kurz erläutert. Als erstes möchte ich Ihnen das Wasserstoff-Atom nach dem Orbitalmodell vorstellen.
Das H-Atom nach dem Orbitalmodell
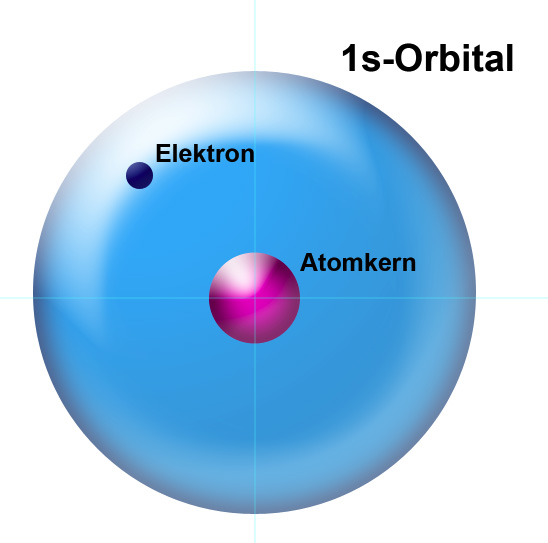
Es könnte sich bei der Zeichnung auch um die Darstellung des H-Atoms nach dem Kugelwolkenmodell handeln, lediglich der Begriff Kugelwolke wurde durch den Begriff Orbital ersetzt, genauer gesagt, durch die Bezeichnung 1s-Orbital.
Was heißt Orbital?
Unter einem Orbital verstehen wir den Raumbereich, in dem wir ein Elektron mit einer bestimmten Wahrscheinlichkeit antreffen können.
Eigentlich müsste man ein Orbital so zeichnen, dass man keine scharfe Grenze erkennen kann. Die Aufenthaltswahrscheinlichkeit des Elektrons nimmt nach außen hin langsam und kontinuierlich ab, nicht schlagartig. Will man allerdings den Raum kennzeichnen, in dem sich ein Elektron mit einer bestimmten Wahrscheinlichkeit aufhält, sagen wir mal zu 99%, so kann man diesen Raum durchaus mit einer scharfen Linie abgrenzen.
Was bedeutet die 1 in dem Begriff 1s-Orbital?
Im Grundzustand befindet sich das Elektron in der ersten Schale, in der K-Schale also. Unter dem Begriff Grundzustand versteht man den energetisch nicht angeregten Zustand des Atoms. Es wurde also keine Energie zum Beispiel in Form von Licht oder Wärme zugeführt. Durch eine Zufuhr von Energie können bestimmte Elektronen auf höhere Energieniveaus befördert werden, aber das spielt hier noch keine Rolle und wird daher nicht näher besprochen.
Was bedeutet das s in dem Begriff 1s-Orbital?
Der Buchstabe s bezeichnet die genaue Art des Orbitals.
Im Kugelwolkenmodell haben die vier Kugelwolken die gleiche Form (nämlich die einer Kugel) und die Elektronen in den vier Kugeln befinden sich alle auf dem gleichen Energieniveau.
Im Orbitalmodell dagegen unterscheidet man verschiedene Typen von Orbitalen. Neben den s-Orbitalen gibt es noch p-Orbitale, d-Orbitale und f-Orbitale. Für die Chemie der aromatischen Verbindungen und für die Farbstoffchemie sind vor allem die s- und p-Orbitale von Interesse, und daher gehe ich in diesem Exkurs auf die d- und f-Orbitale nicht weiter ein.
Das He-Atom (nach oben)
Betrachten wir das Helium-Atom, so wie es sich nach dem Orbitalmodell darstellt:
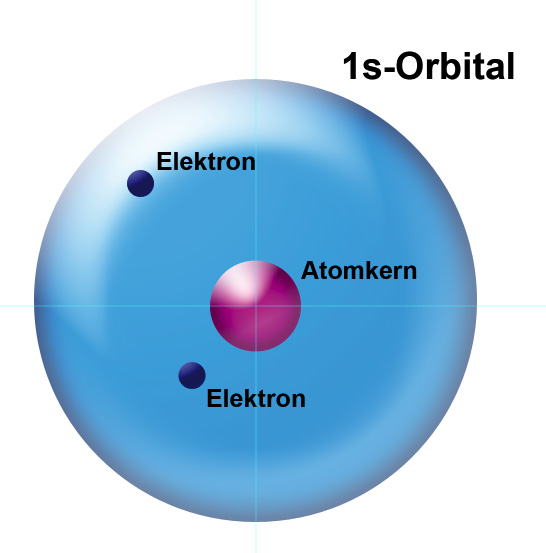
In dem 1s-Orbital des He-Atoms tummeln sich jetzt zwei Elektronen, die sich übrigens durch ihren Spin unterscheiden (Spin = Rotationsrichtung des Elektrons; das eine Elektron dreht sich links herum um seine eigene Achse, das andere Elektron rechts herum).
Mit zwei Elektronen ist das 1s-Orbital voll besetzt. Ein drittes Elektron kann in diesem Orbital nicht mehr untergebracht werden.
Das Li-Atom (nach oben)
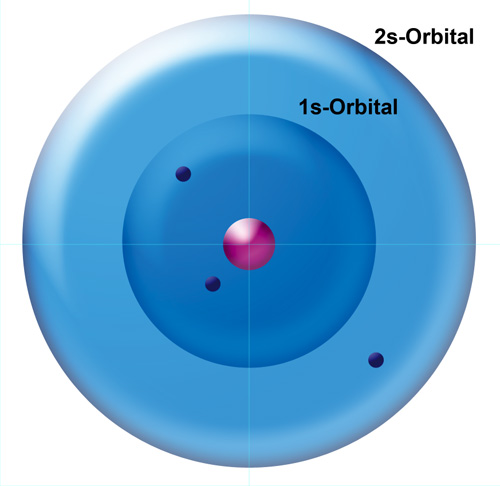
Das dritte Elektron hält sich beim Lithium-Atom in der L-Schale auf, die nach dem Kugelwolkenmodell aus vier gleichartigen Kugelwolken besteht, die tetraedrisch um den Atomkern angeordnet sind. Nach dem Orbitalmodell hält sich das dritte Elektron jedoch in dem 2s-Orbital auf, das kugelsymmetrisch um den Atomkern und das 1s-Orbital angelegt ist. Der Aufenthaltsbereich des dritten Elektrons wird durch die folgende Abbildung sehr gut dargestellt:
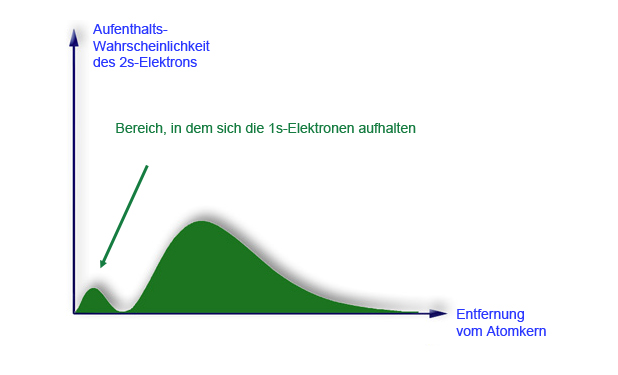
Diese Abbildung zeigt die Aufenthaltswahrscheinlichkeit des 2s-Elektrons in Abhängigkeit von der Entfernung zum Atomkern. Man sieht gut, dass sich das 2s-Elektron auch im Bereich des 1s-Orbitals aufhalten kann, allerdings mit einer sehr geringen Wahrscheinlichkeit.
Das Be-Atom (nach oben)
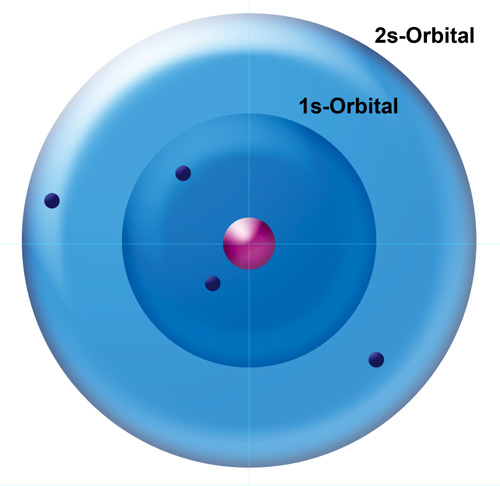
Im Beryllium-Atom haben wir schon vier Elektronen. Nach dem Kugelwolkenmodell hätten wir jetzt auf der L-Schale vier Kugelwolken, von denen je zwei mit einem Elektron besetzt sind. Nach dem Orbitalmodell haben wir auf der L-Schale jedoch ein 2s-Orbital, das mit zwei Elektronen voll besetzt ist:
Das B-Atom (nach oben)
Jetzt wird es wirklich spannend. Bisher hatten wir nur kugelsymmetrische s-Orbitale. Beim Bor-Atom befinden sich drei Elektronen auf der L-Schale, die in zwei verschiedenen Orbitalen untergebracht sind. Zwei Elektronen halten sich in dem 2s-Orbital auf, das dritte Elektron jedoch in einem 2p-Orbital.
Ein p-Orbital ist jedoch nicht kugelförmig, sondern hat die Form einer Hantel.
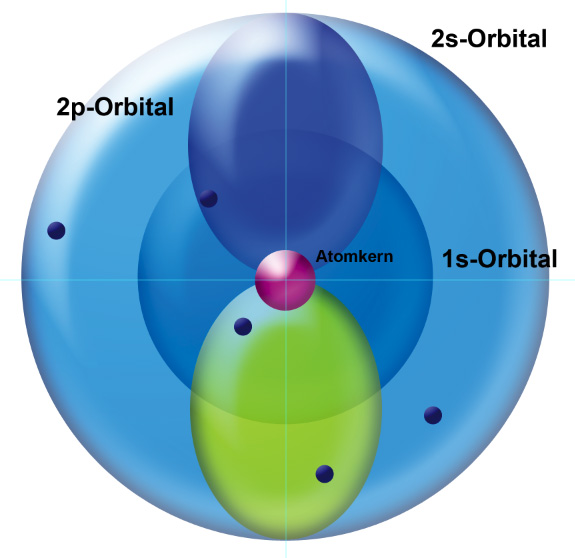
Jetzt denken Sie wahrscheinlich: Aha, da sind doch zwei 2p-Orbitale eingezeichnet, eins in blau, das andere in gelb. Das stimmt nicht! Es handelt sich um ein einziges 2p-Orbital. Die beiden Farben stehen nur für die beiden Orbital-Lappen. Ein p-Orbital besteht nämlich aus zwei Hälften, die als Orbital-Lappen bezeichnet werden.
Für Experten: Der Begriff "Orbital-Lappen"
Um Ihnen dies zu erklären, ist es sinnvoll, mal ein wenig Gitarre zu spielen. Wie Sie ja sicherlich wissen, ist Gitarre spielen eines meiner Hobbys. Nehmen wir uns also eine Gitarre und zupfen wir einmal kräftig an der tiefen E-Saite. Das gibt einen wunderbaren tiefen Ton, und wenn man sich die schwingende Saite einmal genauer ansieht, kann man sehen, dass sie in der Mitte am kräftigsten schwingt. Das ist ja auch logisch, denn oben und unten ist die Saite ja am Hals bzw. am Steg festgemacht, dort kann sie nicht schwingen. Wenn wir uns die schwingende Saite einmal von der Seite ansehen (pun intended), so sehen wir ungefähr folgendes:
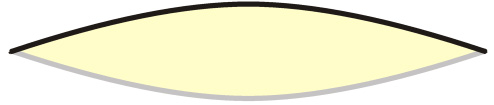
Das ist natürlich stark übertrieben, aber das Entscheidende wird dargestellt: In der Mitte, also beim 12. Bund der Gitarre, schwingt die Saite am stärksten.
Geübte Gitarristen beherrschen die sogenannte Flageolett-Technik. Darunter versteht man das gezielte Erzeugen von Obertönen einer schwingenden Saite. Um einen solchen Oberton zu erzeugen, muss man beispielsweise die tiefe E-Seite anzupfen und dann den Zeigefinger der rechten Hand genau auf die Mitte der Seite legen, also da, wo der 12. Bund ist. Man darf die Saite dabei nicht herunterdrücken, sondern muss nur das freie Schwingen unterbinden. Es entsteht dann eine Welle, die von der Seite gesehen ungefähr so aussieht:
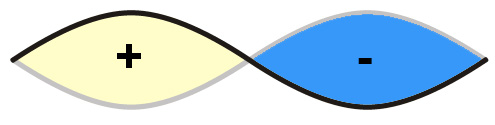
Wir sehen zwei "Schwingungsbäuche", den einen habe ich mit einem Plus-Symbol markiert, den anderen mit einem Minus-Symbol.
Nicht nur Gitarrensaiten können schwingen, sondern auch zweidimensionale Objekte wie zum Beispiel das Fell einer Trommel. Nur sind dann die erzeugten Wellen bzw. Schwingungen ebenfalls zweidimensional.

Chladnische Klangfiguren für Platten
Matemateca (IME USP) / (name of the photographer), CC BY-SA 4.0, via Wikimedia Commons
Dieses Bild zeigt die sogenannten Chladinischen Klangfiguren. Diese interessanten und vielfältigen Formen entstehen, wenn man Sand auf eine schwingende Platte, zum Beispiel ein Trommelfell streut.
"Infolge von Eigenresonanzen beginnt die Platte mit einer ihrer Moden zu schwingen. Der Sand wird beim Tönen der Platte von den vibrierenden Partien lokal weggeschleudert und wandert zu den Stellen, an denen keine oder schwächere Schwingung auftritt. Auf diese Weise werden die Knotenlinien stehender Wellen sichtbar, die sich auf der Platte ausbilden."
Aus dem Wikipedia-Artikel "Chladinische Klangfigur".
Eine gute Vorstellung zweidimensionaler Wellen können Sie übrigens selbst erhalten, wenn Sie einen Stein in einen See werfen. Im Gegensatz zur Gitarrensaite und den Chladinischen Klangfiguren gibt es hier aber keine begrenzenden Randbedingungen, die Welle im See kann sich in zwei Dimensionen frei ausbreiten.
Sich frei ausbreitende dreidimensionale Wellen erhalten Sie, wenn Sie laut in die Hände klatschen, sprechen oder singen. Dann breiten sich nämlich Schallwellen in allen drei Dimensionen aus.
So, nachdem wir jetzt so viel über Wellen gelernt haben, die sich in ein, zwei oder drei Dimensionen ausbreiten, kommen wir wieder zurück zur Quantenphysik.
Zurück zur Quantenphysik
Nach den Vorstellungen der Quantenphysik wird der Zustand eines Elektrons durch eine Wellenfunktion beschrieben. Wenn man diese Funktion quadriert, erhält man die Aufenthaltswahrscheinlichkeit des Elektrons. Man kann also sagen, dass sich Elektronen wie dreidimensionale stehende Wellen verhalten.
Damit hinkt der Vergleich mit dreidimensionalen Schallwellen etwas, denn bei diesen handelt es sich ja nicht um stehende Wellen. Mit den chladinischen Klangfiguren könnte man die "Elektronenwellen" eher vergleichen, obwohl diese ja nur zweidimensional sind.
Die Orbitale, die wir als s-, p-, d- und so weiter bezeichnen, sind nichts anderes als graphische Darstellungen dieser Wellenfunktion bzw. des Quadrats dieser Wellenfunktion (= Aufenthaltswahrscheinlichkeit des Elektrons).
Wellenfunktion und Gitarrensaiten
Um zu verstehen, warum es verschiedene Typen von Orbitalen gibt, muss wieder die alte Gitarrensaite herhalten - obwohl dieser Vergleich etwas hinkt, wie wir gleich noch sehen werden.
Eine Gitarrensaite, die angezupft wird, ohne dass die linke Hand sie berührt, könnte man als Grundzustand dieser Saite bezeichnen. Ähnlich ist ein s-Orbital der Grundzustand einer Elektronenwelle (Grundzustand = niedrigster Energiezustand). Eine Art dreidimensionaler Klangfigur in der Form einer Kugel.
Hält man den Zeigefinger der linken Hand lose in der Höhe des 12. Bundes auf die Saite und zupft diese dann an, erhält man zwei Schwingungsbäuche. Man könnte von einem angeregten Zustand sprechen. Auf ein Elektron übertragen, könnte man ein p-Orbital ebenfalls als angeregten Zustand bezeichnen. In Analogie zur Gitarrensaite kann man das p-Orbital als Zustand mit zwei "Schwingungsbäuchen" sehen, die aber als Orbitallappen bezeichnet werden. Ein Lappen wird als Plus-Lappen bezeichnet, der andere als Minus-Lappen. Das hat übrigens überhaupt nichts mit elektrischen Ladungen zu tun, sondern "Plus" und "Minus" beziehen sich auf das Vorzeichen der Wellenfunktion und nicht auf reale Ladungen.
Entsprechend sind die d- und f-Orbitale weitere angeregte Zustände des Elektrons. Bei einer Gitarrensaite müsste man dazu den linken Finger beim Zupfe auf den 7. oder 5. Bund halten.
Zusammenfassung
Nach der Quantenmechanik wird der Zustand eines Elektrons durch eine dreidimensionale Wellenfunktion beschrieben. Orbitale sind die grafischen Darstellungen derjenigen Bereiche, in denen die Aufenthaltswahrscheinlichkeit des Elektrons besonders groß ist. Die s-Orbitale entsprechen kugelförmigen Grundzuständen ohne Knoten, p-Orbitale dagegen angeregten Zuständen mit einem Knoten, der die beiden sogenannten Orbitallappen voneinander trennt. Die Plus- und Minus-Lappen stehen dabei für die unterschiedlichen Vorzeichen der Wellenfunktion, nicht für elektrische Ladungen.
Kritische Betrachtung des Saiten-Modells
In vielen Chemie-Lehrbüchern wird das Orbitalmodell mit dem Vergleich einer schwingenden Gitarrensaite erklärt. Dieses Bild ist anschaulich, aber physikalisch nicht ganz korrekt.
Bei einer Gitarrensaite entstehen die einzelnen Töne, weil die Saite an beiden Enden festgehalten wird. Diese festen Enden bilden Randbedingungen. Sie erzwingen, dass nur Schwingungen mit bestimmten Wellenlängen und Frequenzen möglich sind. Die Energie der Saite lässt sich jedoch beliebig verändern – sie ist nicht gequantelt.
Im Atom ist das anders: Hier gibt es keine festen Enden und keine äußeren Randbedingungen. Die Schrödinger-Gleichung beschreibt, wie sich ein Elektron im elektrischen Feld des Atomkerns bewegt. Aus dieser Gleichung ergibt sich von selbst, dass nur bestimmte Energiezustände erlaubt sind. Diese Energieniveaus sind diskret – also wirklich gequantelt.
Die Quantisierung der Energie entsteht nicht – wie bei der Saite – durch äußere Randbedingungen, sondern aus der Kombination von Energieerhaltung und der mathematischen Struktur der Schrödinger-Gleichung. Dadurch sind nur bestimmte Werte für die Energie möglich – die sogenannten Eigenwerte. Deshalb kann ein Elektron im Atom nur ganz bestimmte Energien annehmen.
Diese Energie-Quantisierung erklärt auch, warum Atome nur bestimmte Spektrallinien aussenden oder absorbieren – ein zentrales Ergebnis der modernen Physik.
Merke
- Bei der Saite: Quantisiert sind Wellenlängen und Frequenzen, nicht die Energie.
- Im Atom: Quantisiert ist die Energie der Elektronen.
Das C-Atom (nach oben)
Beim Kohlenstoff-Atom haben wir schon vier Elektronen auf der L-Schale, die in Orbitalen untergebracht werden müssen. Nach dem Kugelwolkenmodell befinden sich diese vier Außenelektronen in je einer eigenen Kugelwolke, was die Vierbindigkeit des C-Atoms gut erklärt.
Nach dem Orbitalmodell dagegen hält sich das vierte Elektron in einem zweiten p-Orbital auf:
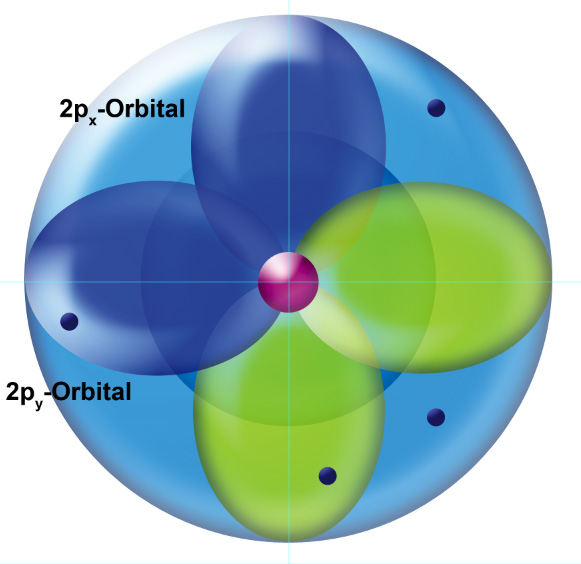
Die Elektronen des 1s-Orbitals habe ich aus Gründen der besseren Übersicht nicht mehr eingezeichnet, in Wirklichkeit sind sie immer noch vorhanden.
Wenn wir mehrere p-Orbitale haben (maximal gibt es drei), so kennzeichnen wir die verschiedenen p-Orbitale mit den Buchstaben x, y und z (in Anlehnung an die drei Achsen eines kartesischen Koordinatensystems). Das dritte Elektron hält sich also im 2px-Orbital auf, das vierte Elektron im 2py-Orbital.
Übrigens müsste das C-Atom nach dem bisher Gesagten eigentlich zweibindig sein; wie wir aber alle wissen, ist es vierbindig. Diese Unstimmigkeit können wir mit dem einfachen Orbitalmodell, wie ich es hier erläutere, noch nicht erklären.
Das N-Atom (nach oben)
Man kann sich die Elektronenkonfiguration des Stickstoff-Atoms auch ohne Zeichnung klar machen:
1s2 2s2 2px1 2py1 2pz1
In dem 1s-Orbital befinden sich zwei Elektronen, in dem 2s-Orbital ebenfalls. Außerdem haben wir auf der L-Schale drei p-Orbitale, die als 2px, 2py und 2pz bezeichnet werden. Jedes dieser drei 2p-Orbitale ist mit einem Elektron besetzt. Das dritte 2p-Orbital, das 2pz-Orbital, ist räumlich an der z-Achse orientiert. Den einen Orbitallappen müssen Sie sich also vor Ihrem Bildschirm vorstellen, der andere Orbitallappen befindet sich hinter Ihrem Bildschirm - hypothetisch gesprochen.
Das O-Atom (nach oben)
Alle drei p-Orbitale sind mit je einem Elektron besetzt. Das sechste Elektron der L-Schale findet nun im 2px-Orbital Platz, dass dann mit zwei Elektronen voll besetzt ist. Beide Elektronen können sich in beiden Orbitallappen aufhalten. Die Elektronenkonfiguration des Sauerstoffs ist daher:
1s2 2s2 2px2 2py1 2pz1
Das F-Atom (nach oben)
Hier die Elektronenkonfiguration:
1s2 2s2 2px2 2py2 2pz1
Das Ne-Atom (nach oben)
Hier die Elektronenkonfiguration:
1s2 2s2 2px2 2py2 2pz2
Die Atome der dritten Periode (nach oben)
Hier wird eine neue Schale "aufgemacht", die M-Schale. Das Außenelektron des Natrium-Atoms befindet sich in einem s-Orbital, nämlich im 3s-Orbital. Daher ist die Elektronenkonfiguration des Na-Atoms:
1s2 2s2 2px2 2py2 2pz2 3s1
Das Mg-Atom hat die Konfiguration
1s2 2s2 2px2 2py2 2pz2 3s2
und das Al-Atom die Konfiguration
1s2 2s2 2px2 2py2 2pz2 3s2 3px1
Die weiteren Konfigurationen der anderen Atome der 3. Periode können Sie sich sicherlich selbst vorstellen.
Da ich diesen Orbitalmodell-Exkurs hauptsächlich für die Seiten der Organischen Chemie geschrieben habe, halte ich es nicht für sinnvoll, an dieser Stelle auf die höheren Orbitale (d und f) einzugehen. Auch die Elektronenkonfigurationen der Nebengruppenelemente wie Eisen werde ich in diesem Exkurs nicht behandeln.