Fitness bei einem monohybriden Erbgang
Stellen wir uns vor, die Fitness (der Fortpflanzungserfolg) eines Hasen hinge allein von seiner Beinlänge ab: zu kurze Beine - und er kann nicht schnell genug Haken schlagen; zu lange Beine - und die Beine behindern ihm beim Rennen. Mittellange Beine wären also bei der Flucht von Vorteil.
Erstmal stellen wir ein Modellsystem auf:
Modellsystem
Eine Hasenpopulation bestehe aus 50 Tieren. Betrachtet werden drei Genotypen mit folgenden Fitness-Werten:
- KK (kurze Beine), Fitness = 0,7
- KL (mittellange Beine), Fitness = 1,0
- LL (lange Beine), Fitness = 0,6
In der Popluation kommen 12 KK-Tiere, 20 KL-Tiere und 18 LL-Tiere vor. Die Populationsfitness beträgt also
(12 x 0,7 + 20 x 1,0 + 18 x 0,6) / 50 = 0,784
Es wäre jetz interessant zu wissen, wie die Populationsfitness W allgemein von den Allelfrequenzenabhängt.
Modellsystem, Fortsetzung
Wir berechnen nun die Allelfrequenzen der beiden Allele K und L in unserer Modellpopulation:
Die 50 Tiere der Population besitzen zusammen 2*12 + 20 = 44 Exemplare des K-Allels und 2*18 + 20 = 56 Exemplare des L-Allels. Die Allelfrequenzen sind also p = 0,44 und q = 0,56 bzw. 44% und 56%.
Wie sähe aber die Populationsfitness bei anderen Allelfrequenzen aus? Angenommen, alle Tiere der Population hätten den Genotyp KK (kurze Beine) mit p = 1. Dann wäre die Populationsfitness FKK gleich 0,7. Hätten alle Tiere den Genotyp LL (lange Beine) mit q = 1 bzw. p = 0, wäre die Populationsfitness FLL gleich 0,6. Wie wir eben schon festgestellt haben, hat unsere Modellpopulation mit p = 0,44 die Fitness 0,78. Stellen wir diese Befunde einmal graphisch dar:
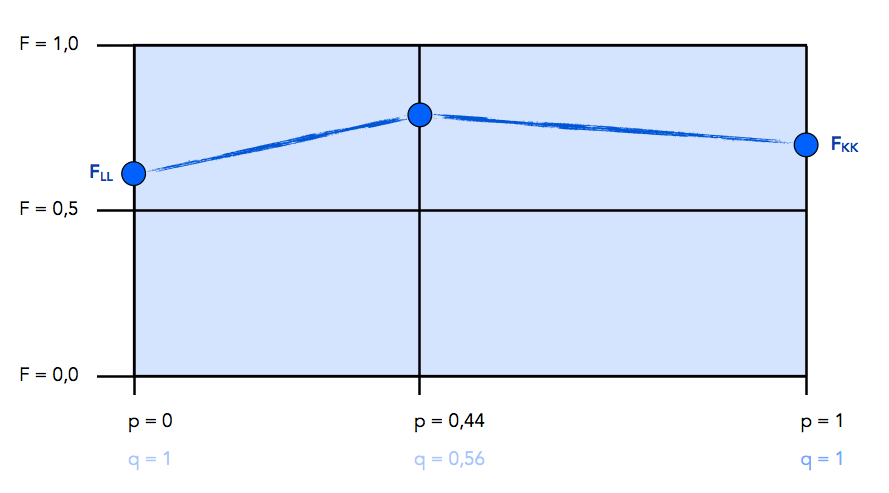
Abhängigkeit der Populationsfitness F von der Allelfrequenz f(K)
Diese Darstellung ist noch nicht sehr schön, da nur drei Werte vorhanden sind, die zudem noch durch Linien verbunden sind. Ein Mathematiker würde das nicht so gut finden, dass man drei diskrete Werte einfach verbindet. Daher wollen wir uns einmal überlegen, ob man die Populationsfitness F nicht aus der Allelfrequenz p berechnen kann, so dass wir eine echte Funktion F = f(p) zeichnen können.
Mit Hilfe des Hardy-Weinberg-Gesetzes kommt man auf die folgende Formel:
F = p2 * FKK + 2pq * FKL + q2 * FLL
Wie bereits gesagt, ist p die Allelfrequenz des einen Allels und q die Allelfrequenz des anderen Allels; immer vorausgesetzt, dass das Gen nur zwei Allele hat. Außerdem gilt dann die Beziehung p+q=1.
Setzen wir in die obige Formel die Werte unseres Modellsystems ein, so bekommen wir:
F = p2 * 0,7 + 2pq + q2 * 0,6
Wollen wir diese Formel graphisch umsetzen, verwenden wir am besten eine Tabellenkalkulation:
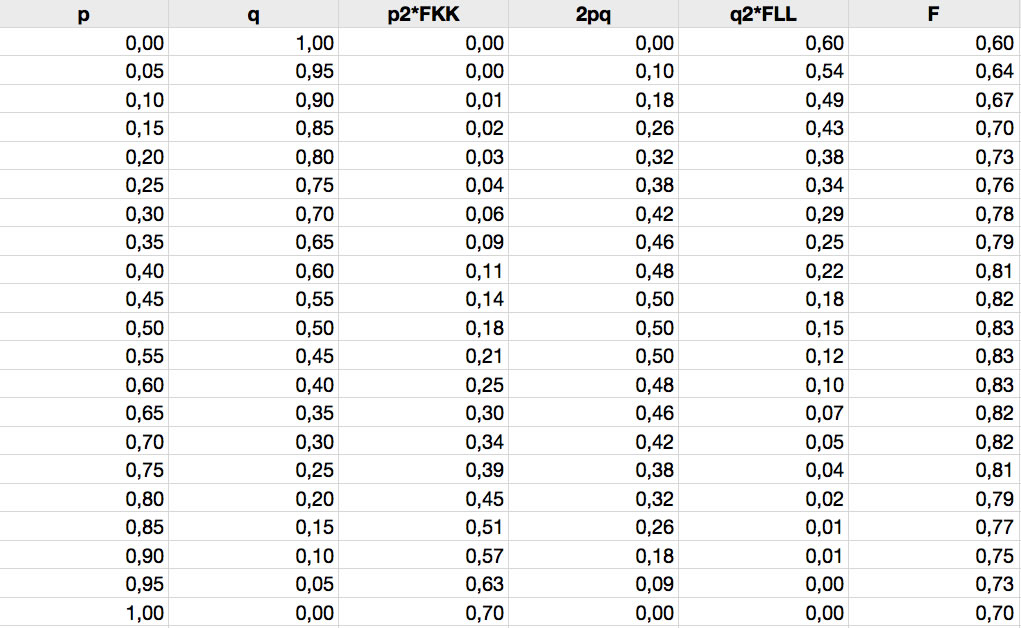
Die Ergebnisse einer Tabellenkalkulation
Jetzt müssen wir die Zahlen aus der Spalte F nur noch gegen die Allelfrequenz p in der Spalte 1 graphisch darstellen.
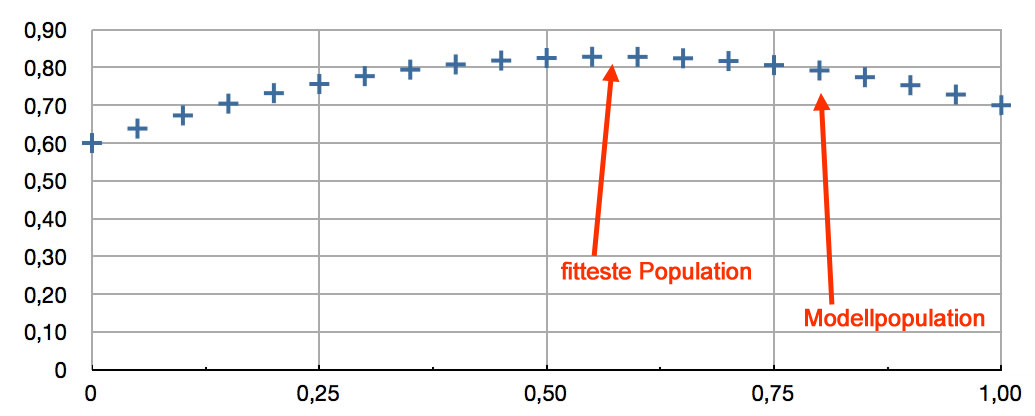
Die graphische Darstellung als xy-Diagramm
Man sieht hier eindeutig, dass die maximale Fitness der Population bei p = 0,55 liegt. Eine Population mit dieser Allelfrequenz wäre also unserer Modellpopulation mit p = 0,78 überlegen, was die Fitness angeht. Unsere Modellpopulation kann also noch "besser" werden, was die Fitness angeht.
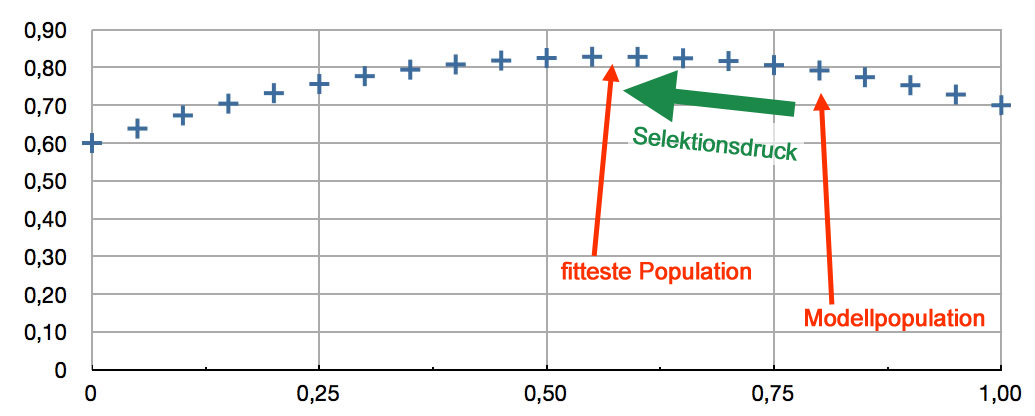
Selektion bewirkt höhere Fitness der Population
Im Laufe der Zeit wird die natürliche Auslese dafür sorgen, dass die Fitness der Population dem Maximum in dieser adaptiven Landschaft zustrebt. Man bezeichnet solche Graphiken, in denen die Fitness einer Population gegen die Frequenz von einem oder zwei Allelen dargestellt ist, in der Tat als adaptive Landschaften. Dieser Begriff wurde von Sewall Wright 1932 eingeführt.
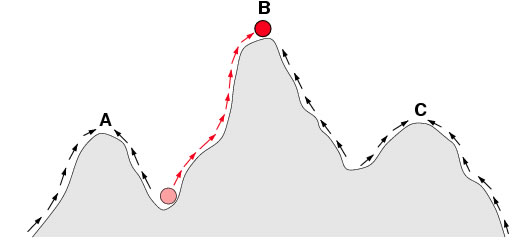
Skizze einer etwas komplexeren Fitness-Landschaft
Quelle: Wikipedia, Autor: Wilke, Lizenz: public domain
Dieses Bild aus der Wikipedia [2] zeigt eine etwas komplexere adaptive Landschaft mit drei Gipfeln A, B und C und zwei Tälern zwischen diesen Gipfeln. Die Population, um die es geht, ist durch den kleinen rosafarbenen Kreis dargestellt, sie befindet sich gerade in einem Fitness-Tal. Die Selektion kann diese Population nun entweder auf den nahe liegenden Gipfel A befördern, was ja schon mal eine deutliche Verbesserung der Populationsfitness darstellt. Dummerweise ist der Population dann der Weg zum deutlich höheren Gipfel B versperrt; sie ist quasi in einem nicht optimalen Fitnessgipfel gefangen. Um von A nach B zu gelangen, wäre eine Art "Gipfelwechsel" notwendig. Dies kann durch normale Selektion nicht geschehen, wohl aber durch drastischere Eingriffe wie zum Beispiel Gendrift, also Zufallsereignisse, welche die genetische Zusammensetzung der Population in einem Schritt gewaltig ändern.
Der Wikipedia-Artikel nennt hier als Beispiel eines nicht möglichen Gipfelwechsels die Wale, die zwar an das Leben im Wasser angepasst sind, aber immer noch Lungen haben (Gipfel A). Dass Wale plötzlich oder auch langfristig Kiemen entwickeln, weil sie dann noch besser angepasst wären (Gipfel B) ist unmöglich, zumindest nach der gängigen Evolutionstheorie.
Dreidimensionale adaptive Landschaften
Hängt die Populationsfitness von zwei Genen mit je zwei Allelen ab, so kann man eine dreidimensionale adaptive Landschaft erstellen. Auf der Achse, die nach rechts zeigt, wird die Allelfrequenz p des erstens Gens dargestellt, auf der Achse, die nach hinten zeigt, wird die Allelfrequenz r des zweiten Gens dargestellt. Auf der Achse, die nach oben zeigt, wird die Populationsfitness W aufgetragen.
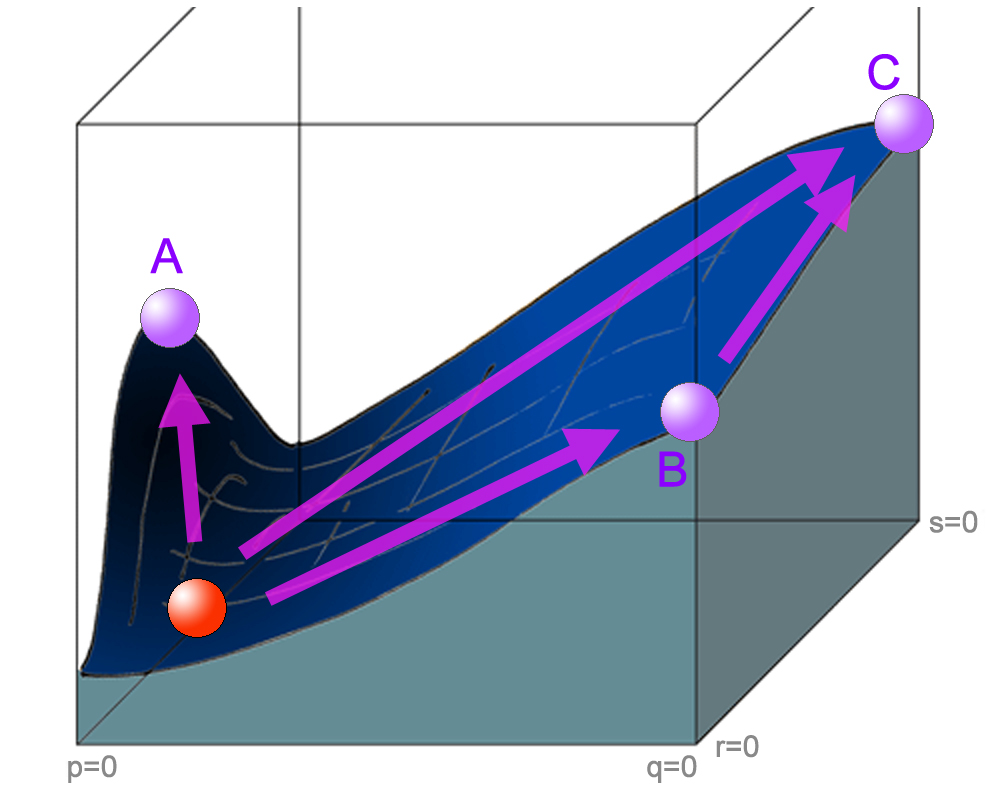
Eine dreidimensionale adaptive Landschaft
Die Population befindet sich gerade in einem Fitness-Tal (roter Ball). Durch adaptive Evolution wäre ein langsames Hinaufsteigen auf einen der drei Gipfel A, B oder C möglich.
"Die Evolution kann adaptive Eigenschaften der Organismen hervorbringen, aber üblicherweise nur allmählich, in kleinen Schritten, mit vielen Übergangsgliedern. Jeder dieser 'Zwischenschritte' muss natürlich ein realer, lebender und sich fortpflanzender Organismus sein. Jeder 'Zwischenschritt' muss lebensfähig sein, und dies zumindest genauso gut wie, wenn nicht sogar besser als sein Vorgänger." [1]
Die Gipfel in den adaptiven Landschaften können mit noch freien ökologischen Nischen verglichen werden, die im Laufe der Zeit von einer Population besetzt werden können.
Die dreidimensionale adaptive Landschaft ist eine starke Vereinfachung der tatsächlichen Verhältnisse. Die Fitness eines Individuums oder einer Population hängt ja nicht nur von zwei Genen ab, sondern von vielen Tausend Genen.
Quellen:
- Zrzavý, Jan; Burda, Hynek; Storch, David; Begall, Sabine; Mihulka, Stanislav. Evolution (German Edition) (S.12). Springer Berlin Heidelberg. Kindle-Version.
- Wikipedia-Artikel "Evolutionäre Anpassung".