6.3 Die binäre Suche

Inhalt dieser Seite

6.3.1 Der Algorithmus

Die binäre Suche erfolgt nach dem Prinzip "Teile und herrsche". Das heißt, man teilt die zu durchsuchenden Daten in ein mittleres Element und zwei Hälften links und rechts davon. Sollte das mittlere Element mit dem Suchbegriff oder der Suchzahl übereinstimmen, ist die Suche erfolgreich beendet. Andernfalls wird entweder in der linken oder in der rechten Hälfte nach dem gleichen Verfahren weitergesucht.

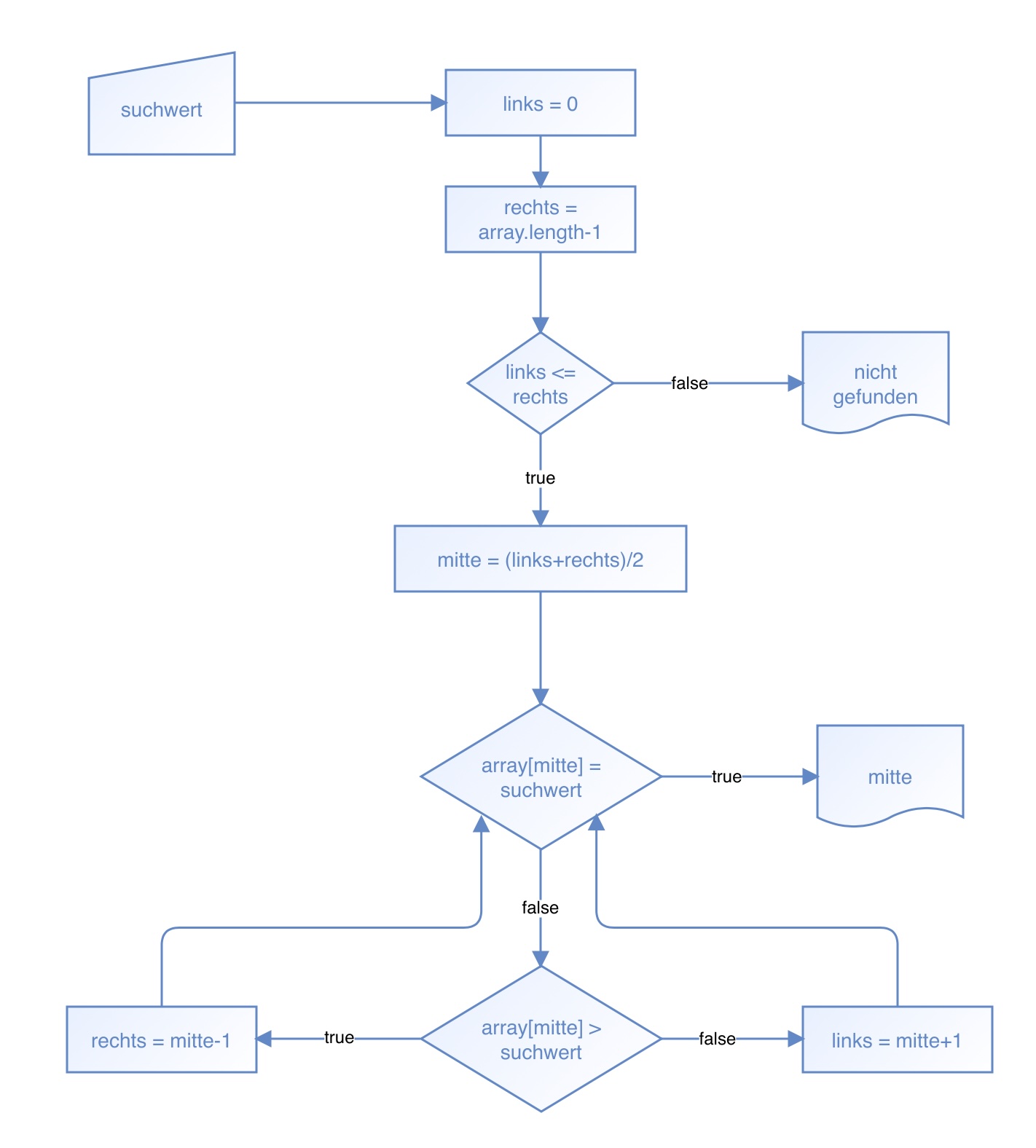
Flussdiagramm der binären Suche
Autor: Ulrich Helmich 2/2026, Lizenz: Public domain

Hier sehen wir ein Flussdiagramm, das den Algorithmus der binären Suche darstellt.

Achten Sie darauf, dass ein Flussdiagramm nicht die Syntax einer Programmiersprache einhalten muss, sondern relativ frei gestaltet werden kann.

6.3.2 Veranschaulichung der binären Suche ↑

Gegeben ist ein int-Array aus 20 Zahlen, die Suchzahl ist 31.

Mit mitte=(links+rechts)/2 berechnen wir den Index des mittleren Elements:

mitte = (0 + 19) / 2 = 9.5

das entspricht dem Index 9 und der Zahl 19:

Die Suchzahl 31 ist größer als 19 (1. Vergleich), das heißt, wir müssen rechts weiter suchen.

Die Zahl 21 an Index 10 ist jetzt die linke Grenze des neuen Suchintervalls, die rechte Grenze bleibt bestehen.

links = mitte + 1

mitte = (10 + 19) / 2 = 14.5

Die Zahl an Index 14, also die 29, ist jetzt die neue mittlere Zahl.

Die Suchzahl 31 ist größer als 29 (2. Vergleich) ⟹ Rechts weiter suchen.

mitte = (15 + 19) / 2 = 17.0

Das entspricht dem Index 17 und der Zahl 35.

Die Suchzahl 31 ist nicht größer als 35 (3. Vergleich) ⟹ Links weiter suchen.

mitte = (15 + 16) / 2 = 15.5

Das entspricht dem Index 15 und der Zahl 31 (4. Vergleich) ⟹ Suchzahl gefunden!

Damit ist die Suchzahl nach nur vier Vergleichen gefunden.

6.3.3 Quantitative Analyse der binären Suche ↑

Mathematiker würden nun eine schöne und komplexe Formel aufstellen, mit der man sofort ausrechnen kann, wie groß die durchschnittliche Suchzeit bei der binären Suche ist.

Informatiker sind da eher praktischer eingestellt. Wir schreiben uns einfach ein kleines Java-Programm, in dem wir ein sortiertes Array einmal sequentiell und einmal binär durchsuchen - und zwar nicht mit einer Suchzahl, sondern mit einer ganzen Reihe von Suchzahlen.

Die Anzahl der Vergleiche in den beiden Methoden wird mitgezählt, um am Ende kommt man zu einem quantitativen Ergebnis für die durchschnittliche Zahl der Vergleiche bei beiden Methoden.

Das Methode zur binären Suche sieht so aus:

    public int vergleicheBinaer(int[] a, int suchzahl)
    {
        int links = 0;
        int rechts = a.length - 1;
        int v = 0;

        while (links <= rechts)
        {
            int mitte = (links + rechts) / 2;

            v++; 
            if (a[mitte] == suchzahl)
            {
                return v;
            }

            v++;
            if (suchzahl < a[mitte])
            {
                rechts = mitte - 1;
            }
            else
            {
                links = mitte + 1;
            }
        }

        return v;
    }

Die lokale Variable v zählt alle Vergleiche mit, die während der Suche anfallen. Die Methode vergleicheBinaer() liefert nicht den Index des gesuchten Elements (oder -1) zurück, sondern die Anzahl der notwendigen Vergleiche zum Finden der Suchzahl bzw. für die Feststellung des Nichtvorhandenseins derselben.

Die Methode für die lineare Suche ist dagegen recht einfach:

    public int vergleicheLinear(int[] a, int suchzahl)
    {
        int v = 0;

        for (int i = 0; i < a.length; i++)
        {
            v++;
            if (a[i] == suchzahl)
            {
                return v;
            }
        }

        return v;
    }

Die Methode ermittleSuchzeit() beginnt folgendermaßen:

    public void ermittleSuchzeit(int arraygroesse)
    {
        int[] zahlen = new int[arraygroesse];

        int vergleicheB = 0; 
        int vergleicheL = 0;

        for (int i=0; i < zahlen.length; i++)
            zahlen[i] = i*2;

Es wird hier ein lokales Array in der angegebenen Größe erstellt. Das Array wird dann mit geraden Zahlen gefüllt, bei einem Array mit 100 Elementen als mit 0, 2, 4, ..., 196, 198.

Mit einer for-Schleife werden dann die Zahlen von 1 bis 64, 1 bis 128, 1 bis 256 etc. in diesem Array gesucht. Die Hälfte der Suchzahlen besteht aus ungeraden Zahlen, die nicht im Array enthalten sind. Dadurch wird die Suche noch realistischer.

Ausgabe des Testprogramms:

Lineare Suche für 64 Zahlen = 2608 Vergleiche
Binaere Suche für 64 Zahlen = 353 Vergleiche
Verhältnis Linear/Binär =         7,39 

Lineare Suche für 128 Zahlen = 10336 Vergleiche
Binaere Suche für 128 Zahlen = 833 Vergleiche
Verhältnis Linear/Binär =        12,41 

Lineare Suche für 256 Zahlen = 41152 Vergleiche
Binaere Suche für 256 Zahlen = 1921 Vergleiche
Verhältnis Linear/Binär =        21,42 

Lineare Suche für 512 Zahlen = 164224 Vergleiche
Binaere Suche für 512 Zahlen = 4353 Vergleiche
Verhältnis Linear/Binär =        37,73 

Lineare Suche für 1024 Zahlen = 656128 Vergleiche
Binaere Suche für 1024 Zahlen = 9729 Vergleiche
Verhältnis Linear/Binär =        67,44 

Lineare Suche für 2048 Zahlen = 2622976 Vergleiche
Binaere Suche für 2048 Zahlen = 21505 Vergleiche
Verhältnis Linear/Binär =       121,97 

Lineare Suche für 4096 Zahlen = 10488832 Vergleiche
Binaere Suche für 4096 Zahlen = 47105 Vergleiche
Verhältnis Linear/Binär =       222,67 

    public int vergleicheBinaerOptimiert(int[] a, int suchzahl)
    {
        int links = 0;
        int rechts = a.length - 1;
        int v = 0;

        while (links <= rechts) {
            int mitte = (links + rechts) / 2;
            v++;
            if      (suchzahl < a[mitte]) rechts = mitte - 1;
            else if (suchzahl > a[mitte]) links  = mitte + 1;
            else return v; // gefunden
        }
        
        return v;
    }

6.3.4 Binäre Suchbäume ↑

Das auf dieser Seite betrachtete binäre Suchverfahren eignet sich sehr gut für bereits sortierte Arrays oder andere Listen. Der zentrale Vorteil des Verfahrens liegt in seiner Effizienz: Durch das wiederholte Halbieren des Arrays kann ein gesuchtes Element in logarithmischer Zeit gefunden werden. Diese Effizienz ist jedoch an eine wesentliche Voraussetzung gebunden: Die Daten müssen bereits sortiert vorliegen und dürfen sich während der Suche nicht verändern.

Was aber, wenn die sortierten Daten ständig durch Einfügen neuer Daten und Löschen nicht mehr benötigter Daten durcheinander gebracht werden? Große Datenbanken können nicht nach jeder Bearbeitung neu sortiert werden, das wäre viel zu aufwendig, und der Vorteil, den die binäre Suche mit sich bringt, wäre wieder zunichte gemacht. Speichert man die Daten dagegen in einem binären Suchbaum, hat man diese Probleme nicht.

Binäre Suchbäume übertragen das Grundprinzip der binären Suche – also das schrittweise Vergleichen und Eingrenzen des Suchbereichs – auf eine dynamische Datenstruktur. Die Ordnung der gespeicherten Werte liegt dabei nicht wie bei einem sortierten Array einfach als feste Reihenfolge vor, sondern ergibt sich aus der Anordnung der Knoten im Baum. Dadurch können Suchen, Einfügen und Löschen von Daten effizient durchgeführt werden, ohne dass die gesamte Struktur jedes Mal neu sortiert werden muss.

Ein binärer Suchbaum mit vier Ebenen
Autor: Ulrich Helmich 03/2026, Lizenz: Public domain

Dieses Bild zeigt einen binären Suchbaum. In einem solchen Baum sind alle Elemente im linken Teilbaum eines Knotens kleiner oder gleich dem Element des Knotens selbst, während alle Elemente im rechten Teilbaum größer sind. Die Daten sind daher bereits suchfreundlich organisiert.

Beispiel 1:

Wir suchen die Zahl 124 und müssen dazu folgende Vergleiche durchführen:

1. Vergleich mit 100 → im rechten Nachfolger der 100 weiter suchen
2. Vergleich mit 145 → im linken Nachfolger der 145 weiter suchen
3. Vergleich mit 120 → im rechten Nachfolger der 120 weiter suchen
4. Vergleich mit 124 → Suchzahl gefunden nach vier Vergleichen.

Beispiel 2:

Wir suchen die Zahl 125 und müssen dazu folgende Vergleiche durchführen:

1. Vergleich mit 100 → im rechten Nachfolger der 100 weiter suchen
2. Vergleich mit 145 → im linken Nachfolger der 145 weiter suchen
3. Vergleich mit 120 → im rechten Nachfolger der 120 weiter suchen
4. Vergleich mit 124 → im rechten Nachfolger der 124 weiter suchen

Es existiert kein rechter Nachfolger der 124, das heißt, die Suchzahl ist nicht im Baum enthalten!

Die hohe Geschwindigkeit der Suche in einem binären Suchbaum liegt darin begründet, dass mit jeder Entscheidung die Anzahl der noch zu durchsuchenden Elemente ungefähr halbiert wird. Dadurch wird jede Zahl im oben dargestellten Baum oder die Feststellung ihrer Abwesenheit nach maximal vier Vergleichen getroffen.

Das Zeitverhalten der Suche in einem binären Suchbaum ist O(log(N)).

Betrachten wir unseren Suchbaum in der Abbildung mit 15 Elementen: Der Zweierlogarithmus von 16 ist 4. Ein binärer Suchbaum mit 31 Elementen hätte eine zusätzliche Ebene, wodurch jede Zahl nach maximal fünf Vergleichen gefunden würde. Bei einem Suchbaum mit 63 Elementen wären es maximal sechs Vergleiche.

Die gesamte Bevölkerung Deutschlands könnte man mit maximal 28 Vergleichen in einem binären Suchbaum finden, wenn es denn einen solchen gäbe.

6.3.5 B-Bäume ↑

Für sehr große Datenmengen, insbesondere wenn diese nicht vollständig im Hauptspeicher gehalten werden können, stoßen einfache binäre Suchbäume allerdings an ihre Grenzen. Hier kommen die von Rudolf Bayer und Edward McCreight Anfang der 70er Jahre entwickelten B-Bäume ins Spiel. Diese B-Bäume erweitern das Konzept des Suchbaums, sodass auch in externen Speichern wie Festplatten oder SSDs effizient gesucht werden kann. B-Bäume bilden sozusagen das Fundament moderner Datenbank- und Dateisysteme.

Ein B-Baum ist ein ausgeglichener Suchbaum, bei dem jeder Knoten maximal N Werte und N+1 Nachfolger-Knoten enthalten darf, wodurch die Baumhöhe gering bleibt und er besonders effizient für den Einsatz in Datenbanken und Dateisystemen geeignet ist.

Ein einfacher B-Baum
Autor: Ulrich Helmich 03/2026, Lizenz: Public domain

Dieses Bild zeigt einen einfachen B-Baum mit N = 3.