5.8 Rekursion

Was versteht man unter Rekursion?

Unter Rekursion versteht man in der Informatik eine Technik, bei der eine Methode sich selbst aufruft, um ein Problem in kleinere Teilprobleme zu zerlegen. Die Grundidee lautet: Ein großes Problem lässt sich oft lösen, indem man es auf eine kleinere Version desselben Problems zurückführt.

Wir haben ein ähnliches Verfahren bereits bei der "Optimierung" des Bubblesorts kennengelernt. Wenn wir das Array in zwei Teilarrays zerlegen, jedes Teilarray sortieren und dann die beiden sortierten Teilarrays mit einer merge()-Methode wieder zusammenfügen, dann halbiert sich die Rechenzeit. Würde man beide Teilarrays noch einmal in je zwei Teilarrays aufteilen, würde sich die Rechenzeit noch einmal halbieren. Auch hier haben wir ein großes Problem in zwei bzw. sogar vier Teilprobleme zerlegt. Eine Rekursion war dieses Verfahren allerdings noch nicht.

Beispiel Fakultät

Bevor wir uns mit den theoretischen Grundlagen der Rekursion weiter befassen, wollen wir uns ein kleines Beispiel anschauen, wie es in fast jedem Schulbuch vorkommt: Die Berechnung der Fakultät einer Zahl.

public int fakultaet(int n)
{
    if (n == 0)
        return 1;
    else
        return n * fakultaet(n - 1);
}

Wird die Methode fakultaet(int n) mit dem Anfangswert n = 4 aufgerufen, so beginnt ein schrittweiser rekursiver Abstieg. Dabei ruft die Methode sich selbst mit jeweils um 1 verringerten Argumenten auf. Die Methode arbeitet also nicht sofort das Endergebnis aus, sondern zerlegt das Problem in immer kleinere Teilprobleme.

Der rekursive Abstieg

Betrachten wir diesen rekursiven Abstieg einmal im Bild:

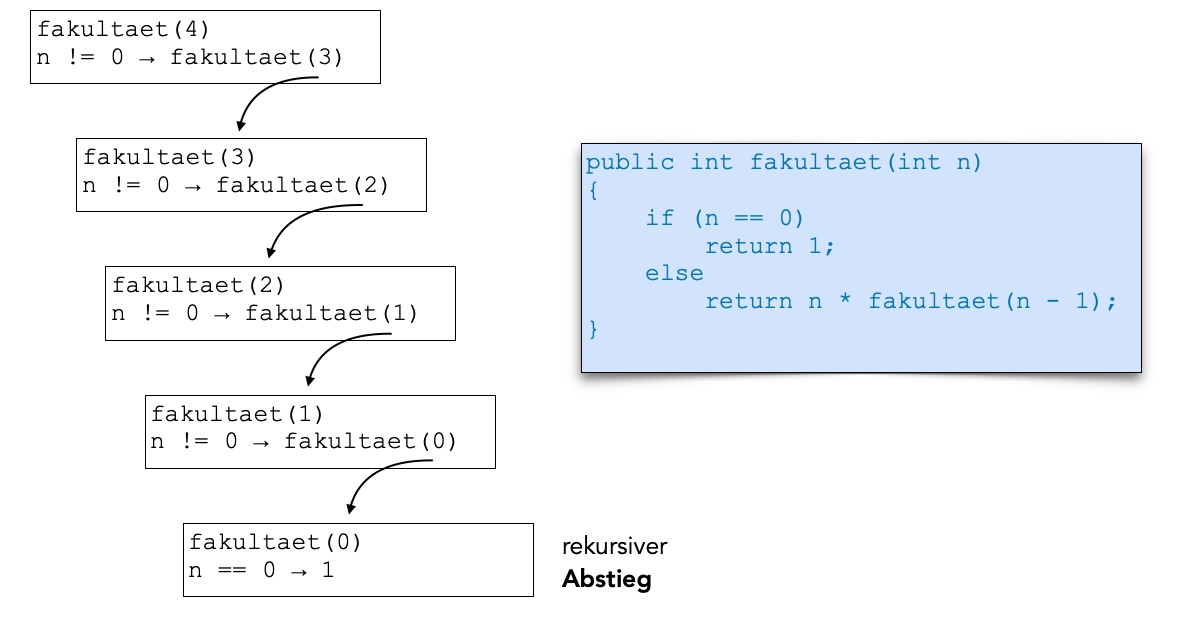
Rekursiver Abstieg bei der Ausführung von fakultaet(4)
Autor: Ulrich Helmich 11/2025, Lizenz: Public domain

Dieser Ablauf lässt sich wie folgt beschreiben:

1. Erster Aufruf: fakultaet(4)

   Die Abbruchbedingung n == 0 ist nicht erfüllt.

   Die Methode möchte 4 * fakultaet(3) berechnen.

   Dafür wird fakultaet(3) aufgerufen.

2. Zweiter Aufruf: fakultaet(3)

   Auch hier ist die Abbruchbedingung nicht erreicht.

   Die Methode möchte 3 * fakultaet(2) berechnen.

   Deshalb ruft sie fakultaet(2) auf.

3. Dritter Aufruf: fakultaet(2)

   Die Methode möchte 2 * fakultaet(1) berechnen.

   Der nächste rekursive Aufruf erfolgt: fakultaet(1).

4. Vierter Aufruf: fakultaet(1)

   Die Methode möchte 1 * fakultaet(0) berechnen.

   Es folgt der Aufruf von fakultaet(0).

5. Fünfter Aufruf: fakultaet(0)

   Jetzt ist die Abbruchbedingung erfüllt: n == 0.

   Die Methode liefert den Wert 1 zurück.

   An dieser Stelle ist der rekursive Abstieg abgeschlossen.

Bis zu diesem Punkt ist noch kein Ergebnis ausgerechnet worden – es wurde lediglich immer weiter "nach unten" gegangen, bis der einfachste Fall (der sogenannte Basisfall bzw. die Abbruchbedingung) erreicht war. Erst danach beginnen die Rückgabewerte Schritt für Schritt nach oben zu "wandern", sodass schließlich das Gesamtergebnis entstehen kann.

Das "Wandern" nach oben wird übrigens als rekursiver Aufstieg bezeichnet.

Der rekursive Aufstieg

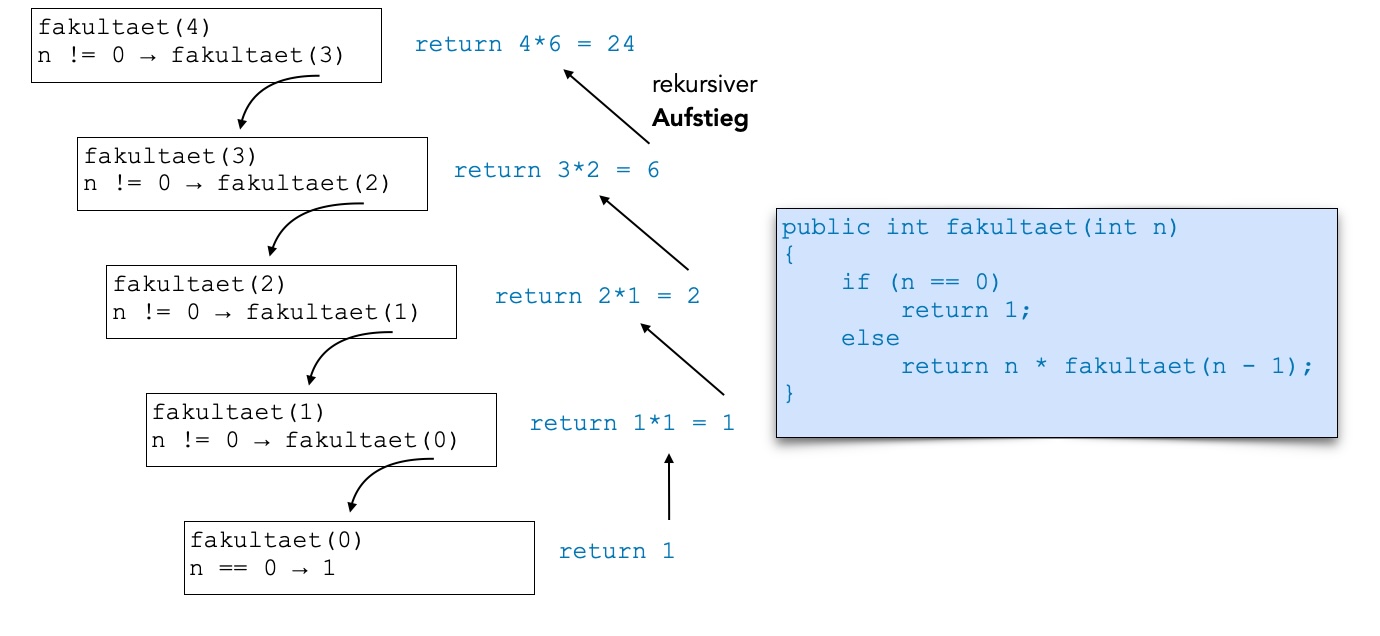
Rekursiver Aufstieg bei der Ermittlung von fakultaet(4)
Autor: Ulrich Helmich 11/2025, Lizenz: Public domain

Nachdem der rekursive Abstieg den Basisfall fakultaet(0) erreicht hat und dieser den Wert 1 zurückliefert, beginnt der rekursive Aufstieg. In dieser Phase werden die zuvor "offenen" Multiplikationen nacheinander ausgewertet. Jede Methode, die während des Abstiegs auf einen Rückgabewert gewartet hat, kann nun ihre eigene Berechnung abschließen und ihrerseits einen Wert an den vorherigen Aufrufer zurückgeben.

Der rekursive Aufstiegt sieht wie folgt aus:

1. Rückkehr aus fakultaet(0)

   fakultaet(0) liefert den Wert 1.

   Nun kann fakultaet(1) berechnen:

   1 * 1 = 1

   und liefert 1 zurück.

2. Rückkehr aus fakultaet(1)

   fakultaet(1) hat nun den Wert 1 geliefert.

   Jetzt kann fakultaet(2) seine Berechnung abschließen:

   2 * 1 = 2

   und liefert 2 zurück.

3. Rückkehr aus fakultaet(2)

   fakultaet(2) gibt den Wert 2 an seinen Aufrufer.

   Dadurch kann fakultaet(3) ausrechnen:

   3 * 2 = 6

   und liefert 6 zurück.

4. Rückkehr aus fakultaet(3)

   fakultaet(3) liefert den Wert 6.

   Damit kann schließlich fakultaet(4) als oberster Aufruf seine Berechnung durchführen:

   4 * 6 = 24

   und gibt 24 zurück.

Beispiel Fibonacci-Zahlen

Die Fibonacci-Zahlen bilden eine bekannte Folge natürlicher Zahlen, die sich durch ein einfaches rekursives Bildungsgesetz auszeichnet. Jede Zahl der Folge ergibt sich als Summe der beiden vorhergehenden Zahlen:

1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 24 - 55 - 89 - 144 - 233 - 377 - ...

Beginnt man mit den Startwerten 1 und 1, entsteht eine Zahlenreihe, die zunächst unscheinbar wirkt, aber in Mathematik, Informatik, Naturwissenschaften und sogar in biologischen Wachstumsprozessen eine bemerkenswerte Rolle spielt.

Hier eine Java-Methode zur Berechnung von fib(n):

public int fib(int n)
{
    if (n == 0)
        return 0;
    if (n == 1)
        return 1;

    return fib(n-1) + fib(n-2);
}

Wenn n den Wert 0 hat, wird die Methode mit 0 beendet, und wenn n den Wert 1 hat, wird die Methode auch sofort beendet und der Wert 1 zurückgegeben. Erst wenn n größer ist als 1, findet ein rekursiver Aufruf statt. Dabei ruft sich die Methode sogar zweimal selbst auf: Einmal für n-1 (dem Vorgänger von n), und einmal für n-2 (dem Vorgänger des Vorgängers). Das funktioniert logischerweise nur dann, wenn n mindestens den Wert 2 hat. Negative Zahlen kommen in der Fibonacci-Folge nämlich nicht vor.

Hier eine noch kompaktere Formulierung der Methode:

public int fib(int n)
{
    if (n < 2)
        return n;
    return fib(n - 1) + fib(n - 2);
}

Hier sehen wir einen Aufruf von fib(4) im Bild:

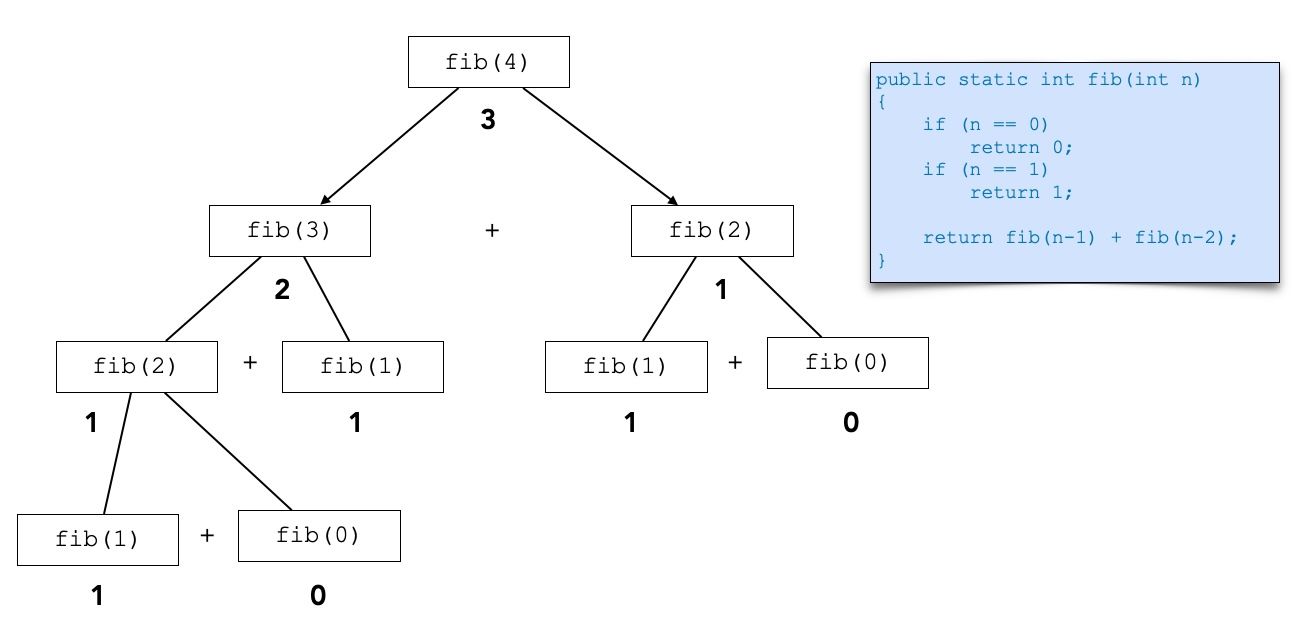
Der Aufruf von fib(4) im Bild
Autor: Ulrich Helmich 11/2025, Lizenz: Public domain

Effizienz-Betrachtungen zur Fibonacci-Folge

Der rekursive Aufruf der Fibonacci-Funktion ist nicht sehr effizient, wenn man der Fachliteratur glauben kann. Der Grund für die Ineffizienz ist die enorme Anzahl von überflüssigen Berechnungen. Bereits in der kleinen Zeichnung für fib(4) kann man sehen, dass fib(1) dreimal aufgerufen werden muss, fib(0) und fib(2) werden je zweimal aufgerufen.

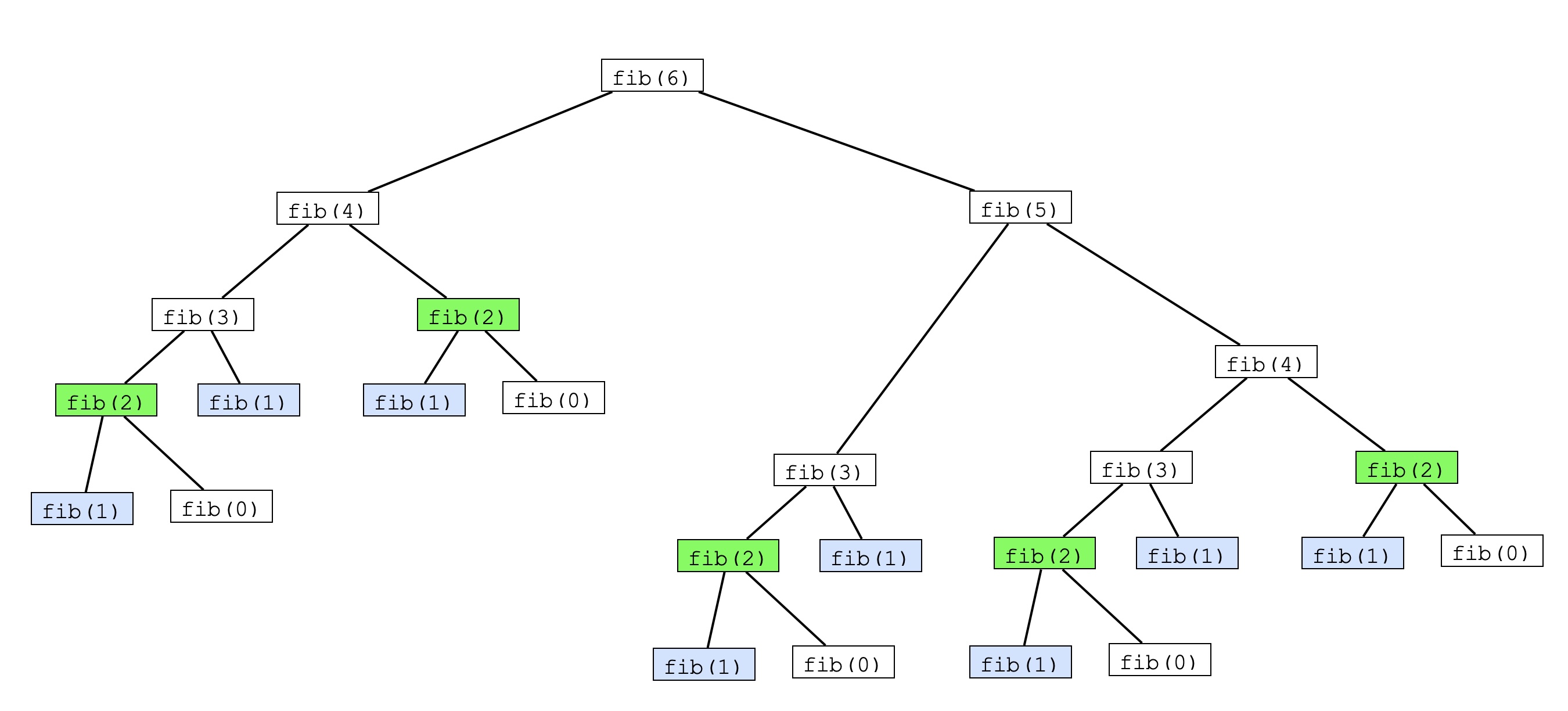
Der Aufruf von fib(6)
Autor: Ulrich Helmich 11/2025, Lizenz: Public domain

Dieses Bild zeigt den Aufruf von fib(6). Um fib(6) zu berechnen, muss bei dem rekursiven Verfahren fib(1) acht mal aufgerufen werden - es muss acht mal die selbe Berechnung durchgeführt werden. Und fib(2) muss fünf mal aufgerufen werden. Das ist nicht sehr effizient.

Nicht-rekursive Methode für die Fibonacci-Zahlen

Eine nicht-rekursive Methode lässt sich mithilfe einer for-Schleife sehr schnell erstellen:

public int fib(int n)
{
    if (n < 2)
        return 1;

    int a = 1;   // fib(0)
    int b = 1;   // fib(1)

    for (int i = 2; i <= n; i++)
    {
        int summe = a + b;
        a = b;
        b = summe;
    }

    return b;
}

Die Methode arbeitet iterativ, also mit einer Schleife statt mit Rekursion.

Sie speichert immer nur die beiden zuletzt berechneten Fibonacci-Zahlen (a und b) und bildet daraus den nächsten Wert. Der Speicherbedarf bleibt konstant, und es werden ausschließlich lineare viele Schritte ausgeführt.