Einführung
Text erstellt von ChatGPT und von mir dann leicht überarbeitet.
In der Informatik spielen Zahlensysteme eine zentrale Rolle, weil Computer intern ausschließlich mit Zahlen arbeiten – genauer gesagt, mit Zahlen im Dualsystem (auch Binärsystem genannt). Um zu verstehen, wie Daten und Befehle im Rechner dargestellt werden, ist ein solides Verständnis der verschiedenen Zahlensysteme notwendig.
Das heute im Alltag verwendete Dezimalsystem (Basis 10) ist uns vertraut, da es auf zehn verschiedenen Ziffern (0 bis 9) beruht. Dieses System ist uns vertraut, weil wir bereits als Kleinkinder Zahlen mit den 10 Fingern abgezählt haben. In der Informatik sind jedoch andere Systeme gebräuchlich, insbesondere das Dualsystem (Basis 2) und das Hexadezimalsystem (Basis 16).
Grundprinzip
Ein Zahlensystem wird durch seine sogenannte Basis charakterisiert. Das Dezimalsystem beispielsweise hat die Basis 10, das Dualsystem die Basis 2 und das Hexadezimalsystem die Basis 16. Diese Basis gibt an, wie viele verschiedene Ziffern in dem Zahlensystem existieren:
Dezimalsystem: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Dualsystem: 0, 1
Hexadezimalsystem: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
An sich hätte man für das Hexadezimalsystem sechs völlig neue Ziffern erfinden können, aber aus technischen Gründen war es anscheinend besser, auf die ersten sechs Buchstaben zurückzugreifen, die auf jeder Tastatur schon vorhanden sind.
Stellenwertsystem am Beispiel des Dezimalsystems
Jede Ziffer in einer Zahl hat einen Stellenwert, der von ihrer Position abhängt. In unserem Dezimalsystem ist die Basis die Zahl 10. Das bedeutet:
- Die Position ganz rechts ist die Einer-Stelle (100 = 1)
- Die Position links daneben ist die Zehner-Stelle (101 = 10)
- Dann kommt die Hunderter-Stelle (102 = 100)
- Dann die Tausender-Stelle (103 = 1000) und so weiter.
So wird im Dezimalsystem die Zahl 1440 folgendermaßen dargestellt:
- 0 an der Einer-Stelle
- 4 an der Zehner-Stelle
- 4 an der Hunderter-Stelle
- 1 an der Tausender-Stelle
Wenn man die Ergebnisse addiert, erhält man den Wert der Zahl
1440 = 1 x 103 + 4 * 102 + 4 * 101 + 0 *100
Das Dualsystem
Wie der Name schon andeutet besteht das Dualsystem aus nur zwei Ziffern, der 0 und der 1. Die Dualzahl 10010 kann leicht in einer Dezimalzahl umgewandelt werden, wie im folgenden Kasten näher erläutert wird.
Umrechnung Dual → Dezimal
Beispiel 1
Wir wollen die Dualzahl 10010 in eine Dezimalzahl umwandeln. Ähnlich wie bei dem letzten Beispiel mit dem Dezimalsystem fangen wir ganz rechts an.
- Die Ziffer 0 steht für die Zweierpotenz 20 = 1
- Die Ziffer 1 links daneben steht für die Zweierpotenz 21 = 2
- Die Ziffer 0 links von der 1 steht für 22 = 4
- Die nächste 0 für 23 = 8
- Die 1 ganz links für 24 = 16
Damit kommen wir zum Ausdruck
1 x 24 + 0 x 23 + 0x22 + 1 x 21 + 0 x 20 = 16 + 2 = 18
Es gilt also 100102 = 1810.
Beispiel 2
Wie sieht die Dezimaldarstellung von 11001100 aus?
1 x 27 + 1 x 26 + 1 x 23 + 1 x 22 = 128 + 64 + 8 + 4 = 204.
Das Dualsystem ist für den Computer ideal, weil jede Stelle einer Binärzahl nur zwei Zustände annehmen kann – das entspricht genau den beiden logischen Zuständen "ein" (1) und "aus" (0), die elektronisch leicht darstellbar sind.
Umrechnung Dezimal → Dual
Man teilt die Dezimalzahl wiederholt durch 2 und notiert die Reste in umgekehrter Reihenfolge
Beispiel 1
- 25 / 2 = 12 Rest 1
- 12 / 2 = 6 Rest 0
- 6 / 2 = 3 Rest 0
- 3 / 2 = 1 Rest 1
- 1 / 2 = 0 Rest 1
Wir lesen die Reste jetzt von unten nach oben und haben dann die Ziffern der Dualzahl von links nach rechts: 11001.
Beispiel 2
133 / 2 = 66 Rest 1
66 / 2 = 33 Rest 0
33 / 2 = 16 Rest 1
16 /2 = 8 Rest 0
8 / 2 = 4 Rest 0
4 / 2 = 2 Rest 0
2 / 2 = 1 Rest 0
1 / 2 = 0 Rest 1
Daraus ergibt sich die Dezimalzahl
10000101
Das Hexadezimalsystem
Das Hexadezimalsystem (Basis 16) verwendet sechzehn verschiedene Ziffern:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Die Buchstaben stehen für die Dezimalwerte 10 bis 15:
A = 10, B = 11, C = 12, D = 13, E = 14, F = 15
Umrechnung Hexadezimal → Dezimal
Beispiel 1
4B16 = 4 x 161 + 11 x 160 = 64 + 11 = 7510
Beispiel 2
AFA416 = 10 x 163 + 15 x 162 + 10 x 161 + 4 x 160 =
10 x 4096 + 15 x 128 + 10 x 16 + 4 = 4496410
Das Hexadezimalsystem wird in der Informatik bevorzugt verwendet, weil es eine kompakte Darstellung langer Binärzahlen ermöglicht. Vier Binärstellen entsprechen genau einer Hexadezimalziffer. Hier drei Beispiele:
00002 = 016
01102 = 616
11012 = D16
11112 = F16
Umrechnung Binäre → Hexadezimal
Dazu zerlegt man die Binärzahl in kleine "Happen" mit je vier Ziffern und wandelt dann jeden "Happen" in eine Hexadezimalziffer um.
Beispiel
11110110 = 1111 0110 = F6
Anwendung des Hexadezimalsystems in der Informatik
Maschinencode und Speicheradressen
Prozessoren arbeiten intern mit Binärzahlen. Für Programmierer ist es jedoch einfacher, Speicheradressen, Bitmuster oder Farbwerte in hexadezimaler Form zu lesen (z. B. 0x1A3F).
Farbwerte
Farben werden häufig in Hexadezimalform angegeben, z. B. #FF0000 für reines Rot (R=255, G=0, B=0).
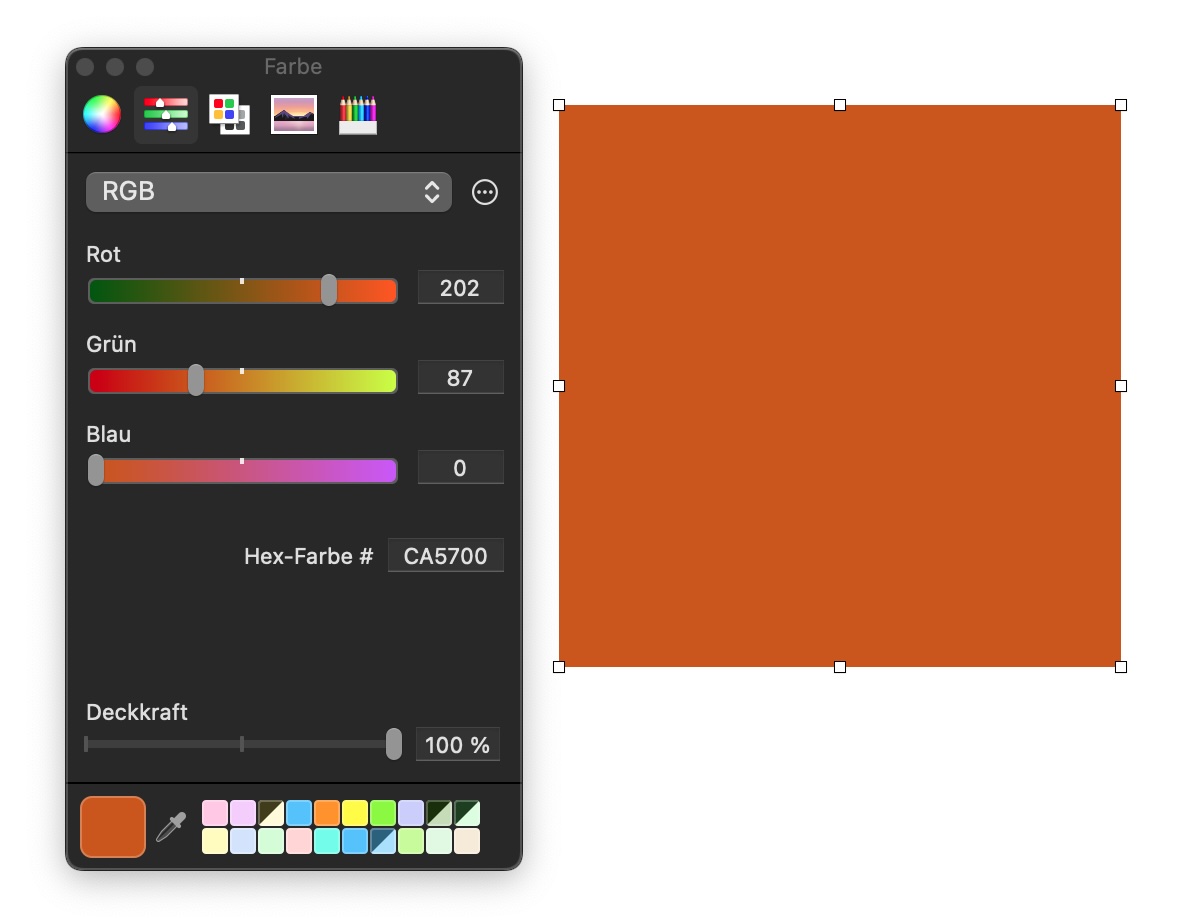
Der Farbwähler von Apple Pages
Autor: Ulrich Helmich 2025, Lizenz: Public domain
Dieses Bild zeigt den Farbwähler des Programms Pages von Apple. Zu sehen ist eine dunkel-orange Farbe mit den RGB-Werten 202,87,0. Angezeigt wird auch die Hex-Farbe CA5700.