Mit Hilfe einer Tabellenkalkulation kann man den Verlauf der elektrischen Leitfähigkeit während einer solchen Leitfähigkeitstitration sehr schön modellhaft simulieren.
Jede Ionensorte trägt zur elektrische Leitfähigkeit einer Elektrolyt-Lösung bei, manche Ionen mehr, manche weniger. Es gibt Ionen, die den Strom besonders gut transportieren können, andere Ionen dagegen leiten den Strom nicht so gut, wie die folgende Tabelle zeigt:
| Ion | relative LF |
| H3O+ | 35 |
| OH- | 19,9 |
| Li+ | 3,9 |
| Na+ | 5,0 |
| K+ | 7,5 |
| Cl- | 7,6 |
Molare Ionenleitfähigkeiten einiger wichtiger Ionen in relativen Einheiten.
Quellen: Wikipedia, Artikel über Molare Leitfähigkeit sowie Buchner, Chemie 2000+, Band 2.
Etwas andere Werte finden sich in dem Buch "Analytische Chemie - Basiswissen III" von Latscha, Linti und Klein (Berlin, Heidelberg, New York 2004):
| Ion | relative LF |
| H3O+ | 314,5 |
| OH- | 173,5 |
| Na+ | 43,4 |
| K+ | 64,5 |
| Cl- | 65,5 |
| Ba2+ | 110 |
Grenzleitfähigkeiten einiger wichtiger Ionen in Wasser bei 18 ºC.
Quellen: Analytische Chemie - Basiswissen III.
Am besten leiten Protonen bzw. Oxonium-Ionen den elektrischen Strom, gefolgt von den Hydroxid-Ionen. Natrium- und Chlorid-Ionen haben dagegen eine recht geringe relative Leitfähigkeit.
Der Beitrag, den ein Ion zur elektrische Leitfähigkeit einer Lösung leisten kann, hängt von mehreren Faktoren ab. Da ist einmal die Beweglichkeit der Ionen. Kleine Ionen können sich besser durch die vielen Wasser-Moleküle bewegen als große Ionen.
Auch von der Ladung selbst hängt die Ionenleitfähigkeit ab. Zweifach positiv geladene Ionen können auch die zweifache elektrische Ladung transportieren, daher ist ihr Beitrag zur elektrische Leitfähigkeit größer als der einfach geladener Ionen (siehe Barium-Ionen), was jetzt aber für unser Modellsystem nicht so wichtig ist, da nur einfach geladene Ionen vorkommen.
In unserem Modellsystem werden 100 ml Natronlauge mit gleichkonzentrierter HCl titriert. In den 100 ml Lauge sollen sich zu Beginn 100 Einheiten Natrium-Ionen und 100 Einheiten Hydroxid-Ionen befinden.
Für diejenigen, die es genau wissen wollen: Wenn man von einer 0,1 molaren Lauge ausgeht, befinden sich in 100 ml dieser Lauge ca. 6 * 1021 Hydroxid-Ionen und genau so viele Natrium-Ionen. Das heißt, eine jede der obigen "Einheiten" steht für 6 * 1019 Ionen.
Die folgende Tabelle zeigt die Veränderung der Ionenverhältnisse, wenn jeweils 10 ml Säure zugegeben worden sind. Die angegebenen Zahlen sind die oben erwähnten "Einheiten". Die Werte der rechten Spalten A und B werden von der Tabellenkalkulation automatisch aus den anderen Werten berechnet.
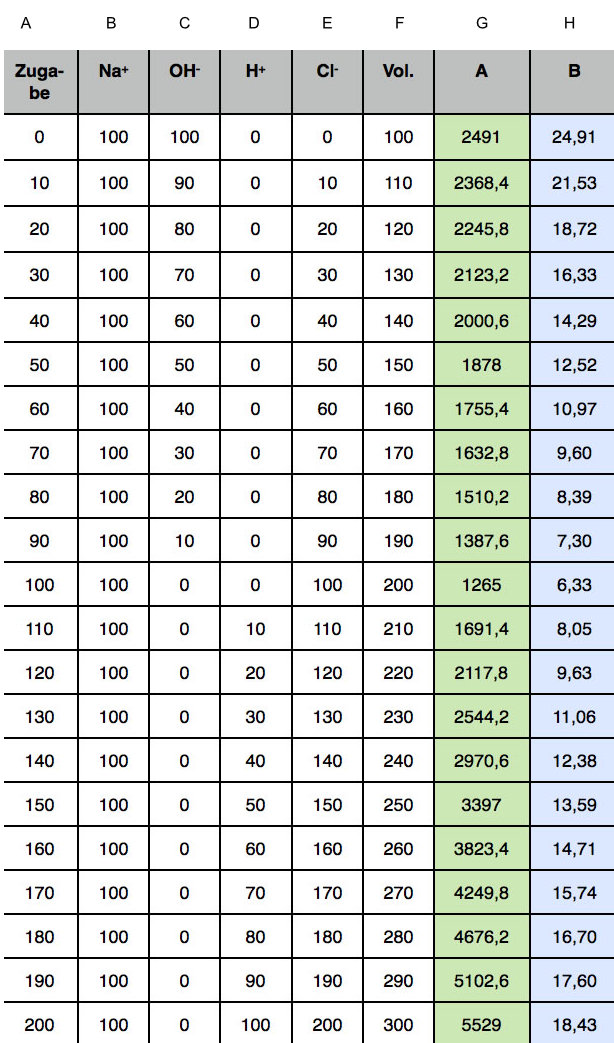
Spalten A - H der Tabellenkalkulation
In der ersten Spalte A sieht man das Volumen der zugegebenen Salzsäure in ml. Insgesamt wurden 200 ml HCl zugegeben.
Die Spalte B zeigt die Stoffmenge n(Na+) der Natrium-Ionen in "Einheiten". 100 ml 1-molarer NaOH enthalten genau 100 Einheiten NaOH, also auch 100 Einheiten Na+-Ionen. Während des gesamten Versuchs bleibt n(Na+) konstant - für die Konzentration c(Na+) gilt dies allerdings nicht, da das Volumen langsam größer wird.
In der Spalte C können wir können wir die Stoffmenge n(OH-) der Hydroxid-Ionen erkennen. Durch die Neutralisationsreaktion geht n(OH-) immer mehr zurück, bis schließlich alle Hydroxid-Ionen bis auf die bekannten 10-7 mol/l bzw. 0 Einheiten neutralisiert sind.
Bei weiterer Zugabe von HCl sinkt die Konzentration der Hydroxid-Ionen noch weiter (Ionenprodukt des Wassers!), aber diese geringen Werte werden im Modellsystem vernachlässigt, daher wurde der Wert 0 in die Zellen der dritten Spalte eingetragen.
In der Spalte D sieht man die Stoffmenge n(H+) der Protonen bzw. Oxonium-Ionen. Solange die Neutralisation noch nicht beendet ist, bleibt n(H+) im Bereich Null (10-7 mol oder weniger sind 0 Einheiten). Nach Erreichen des Äquivalenzpunktes steigt n(H+) jedoch stetig an.
Die Spalte E zeigt die Stoffmenge n(Cl-) der Chlorid-Ionen an. Dieser Wert nimmt stetig zu, da mit jedem Milliliter zugetropfter Salzsäure die Anzahl der Chlorid-Ionen ansteigt und die Chlorid-Ionen an keiner chemischen Reaktion teilnehmen und daher auch nicht verbraucht werden.
Die Spalte F zeigt das zunehmende Volumen der Lösung, das ja bei der Berechnung von Konzentrationen berücksichtigt werden muss.
Die Spalte G zeigt das Ergebnis einer Modell-Berechnung. Am Besten schauen wir uns mal die Berechnungsformel der Tabellenkalkulation an, mit der ich die Modellberechnung durchgeführt habe (AppleWorks 6):
G2 = B2*5.01 + C2*19.9 + D2*35 + E2*7.64
Es werden also die jeweiligen Stoffmengen mit der relativen Leitfähigkeit des entsprechenden Ions multipliziert und das Ganze dann summiert. Hierbei ist aber noch nicht das zunehmende Volumen der Lösung berücksichtigt. Also wird in der letzten Spalte H der so errechnete Wert durch das Volumen der Lösung dividiert, um die relative Leitfähigkeit zu erhalten.
Trägt man jetzt diese Werte der Spalte H gegen die HCl-Zugabe in Spalte A auf, so erhält man einen Graphen, der stark an die im Versuch 10 gewonnenen Daten erinnert.
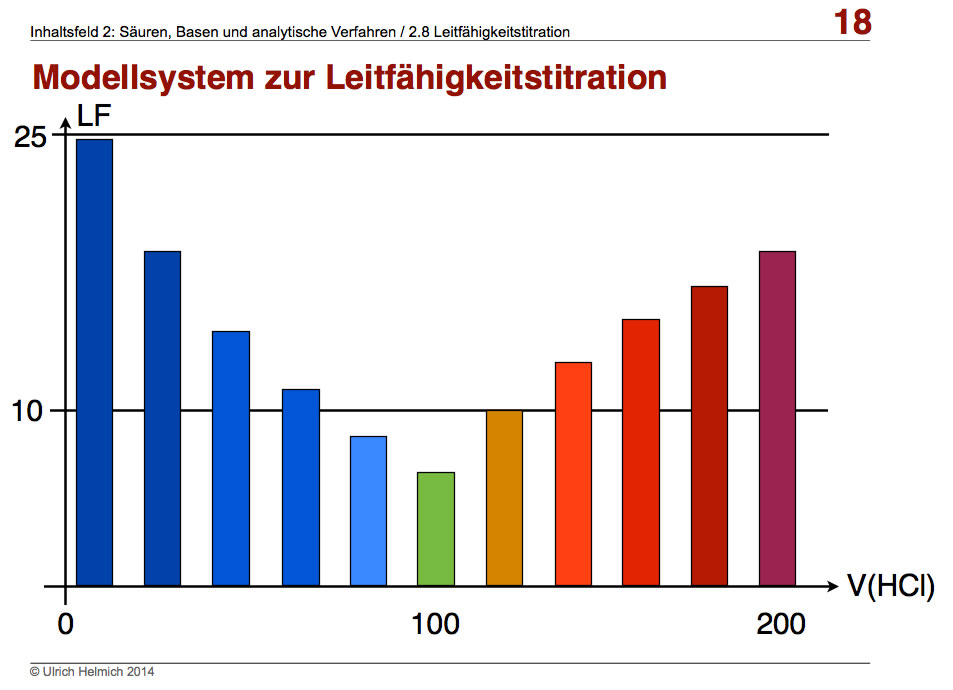
Veränderung der elektrische Leitfähigkeit während der Zugabe von HCl zur NaOH. Nach 100 ml ist der Äquivalenzpunkt erreicht, dann werden weitere 100 ml HCl zugegeben.
Ursachen der hohen Leitfähigkeit der Oxonium- und Hydroxid-Ionen
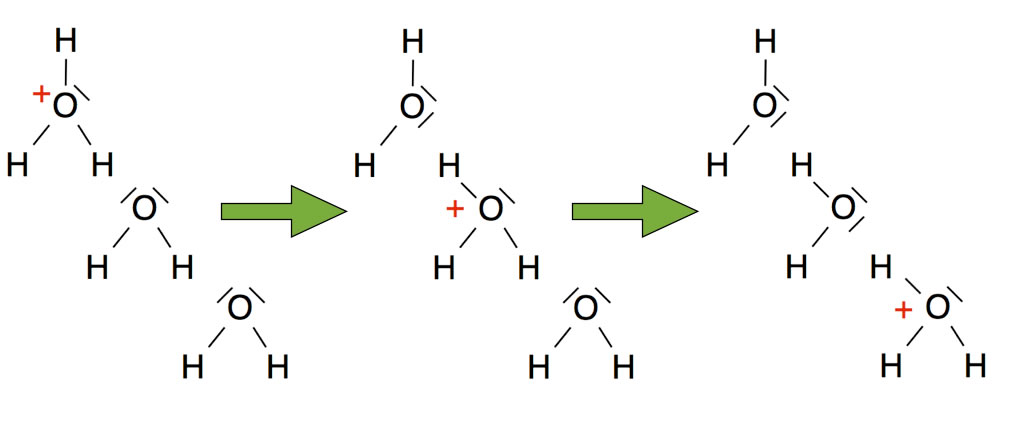
GROTTHUSS-Mechanismus der Weiterleitung positiver Ladungen in Wasser
Auf diesem Bild kann man den nach Theodor GROTTHUSS benannten Mechanismus erkennen, mit dem in einer wässrigen Lösung die positiven Ladungen der Oxonium-Ionen sehr schnell weitergeleitet werden können. Die Oxonium-Ionen müssen nicht wie andere Ionen durch die Lösung diffundieren, sondern die positive Ladung wird einfach an ein anderes Wasser-Molekül weitergereicht. Dies geschieht - einfach gesprochen - durch "Umklappen" der kovalenten Bindungen zwischen den O- und H-Atomen benachbarter Wasser-Moleküle.
Weitere Einzelheiten dazu finden Sie in meinem Lexikon-Artikel "Grotthuss-Mechanismus". Dort steht auch eine kleine Bemerkung zu der wichtigen Frage, wieso eigentlich Oxonium-Ionen eine höhere Äquivalentleitfähigkeit haben als Hydroxid-Ionen.