Der Begriff Diffusion lässt sich am besten mit einem kleinen Versuch erklären: In einen Standzylinder gibt man Leitungswasser. Mit einer längeren Pipette lässt man dann langsam und vorsichtig eine Kaliumpermanganat-Lösung auf den Boden des Standzylinders laufen.
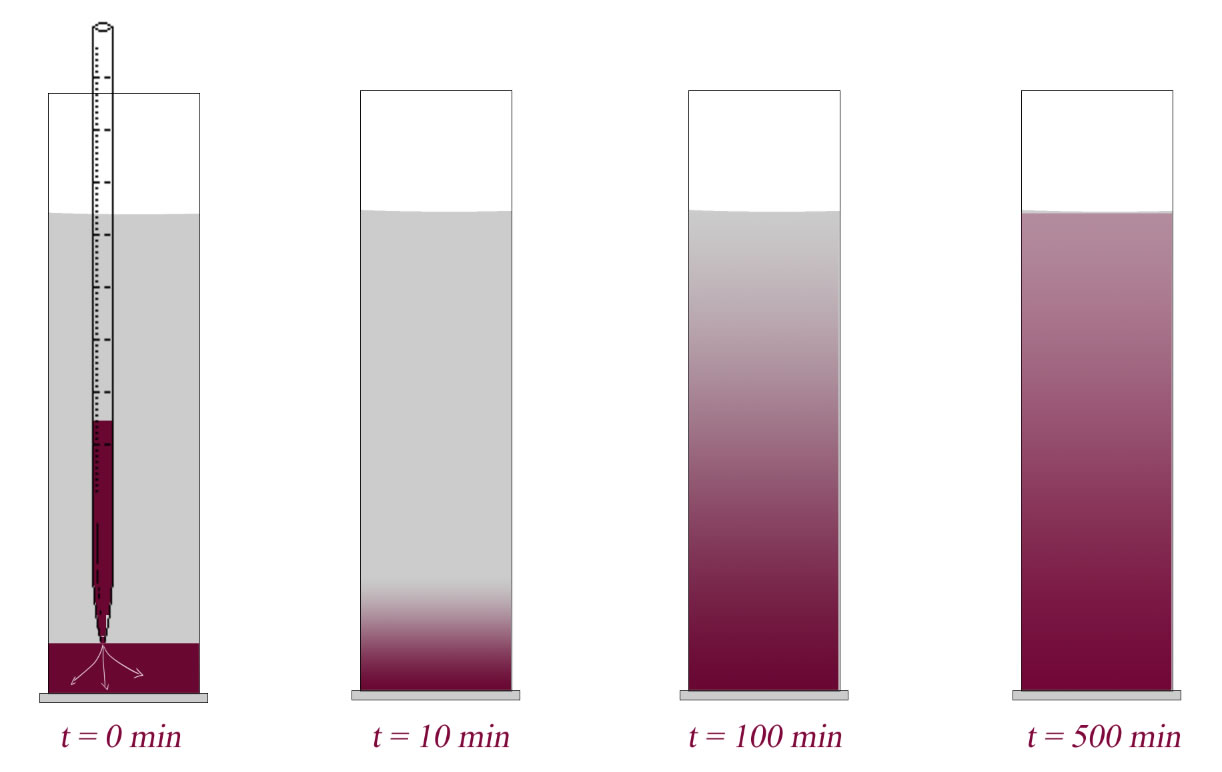
Zu Beginn des Versuchs herrscht bezüglich der Kaliumpermanganat-Teilchen ein großer Konzentrationsunterschied. Auf dem Boden des Zylinders ist c(KMnO4) sehr hoch, oben im Zylinder ist c(KMnO4) = 0.
Im Laufe der Zeit wird der Konzentrationsunterschied zwischen oben und unten aber immer kleiner, am Ende, nach ein paar Stunden oder eventuell sogar erst nach ein paar Tagen, besteht kein Konzentrationsunterschied zwischen dem oberen und dem unteren Bereich des Zylinders, es herrscht ein Zustand, der als Konzentrationsausgleich beschrieben wird.
Ursache für diesen Konzentrationsausgleich ist die Diffusion der Kaliumpermanganat-Teilchen, und die Ursache der Diffusion wiederum ist die BROWNsche Molekularbewegung. Daher soll zunächst dieser wichtige Begriff erläutert werden.
Auf den Cytologie-Seiten meiner Homepage habe ich eine ganze Reihe von Seiten zum Thema Diffusion geschrieben; wenn Sie sich für die Einzelheiten interessieren, schauen Sie sich doch bitte diese Seiten an.
Enthalpie-Änderungen bei einer Diffusion
Wenn gestautes Wasser den Berg herabfließt, kann es Arbeit leisten, zum Beispiel ein Mühlrad antreiben. Das heißt, gestautes Wasser enthält Energie = die Fähigkeit Arbeit zu leisten.
Auch ein Konzentrationgradient stellt einen solchen Energiespeicher dar. Wenn die Teilchen von der Seite der hohen Konzentration auf die Seite der geringen Konzentration diffundieren, können sie dabei Arbeit verrichten. Mitochondrien und Chloroplasten nutzen zum Beispiel die in einem Protonengradienten gespeicherte Energie, um daraus ATP herzustellen, wenn die Protonen zur Seite mit der niedrigen Konzentration durch ein spezielles Enzym diffundieren.
Wie berechnet man nun die in einem Konzentrationsgradienten gespeicherte freie Enthalpie ΔG (so misst man ja in biologischen Systemen normalerweise die Energie).
Hier die entsprechende Formel:
$\Delta G = 2,303 \cdot R\cdot T \ \cdot log \frac{c_{2}}{c_{1}} + z \cdot F \cdot U$
Falls der Browser die Formeln auf dieser Seite nicht richtig darstellt, wurde die Erweiterung MathJax nicht korrekt geladen. Entweder ist der Browser veraltet, oder es besteht im Augenblick keine Internetverbindung.
Dabei gilt:
- R = Gaskonstante = 0,008315 kJ mol-1 K-1
- T = absolute Temperatur in K
- z = elektrische Ladung
- F = Faraday-Konstante = 96,5 kJ mol-1 V-1
- U = Membranpotenzial
Wie viel freie Enthalpie wird nun bei einer Diffusion in Richtung des Konzentrationsgradienten freigesetzt, wenn c1 = 1,0 mol/l beträgt und c2= 0,1 mol/l ? Rechnen wir das zunächst mal für ein ungeladenes Teilchen aus, zum Beispiel für Glucose.
$\Delta G = 2,303 \cdot 0,008315 \frac{kJ}{mol \cdot K} \cdot 298 K \ \cdot log \frac{0,1}{1} + 0 \cdot F \cdot U$
Das Ergebnis dieser Berechnung ist dann ΔG = -5,707 kJ/mol.
Die freie Enthalpie ist negativ, weil ja bei der Diffusion von der Seite der hohen Konzentration zur Seite der niedrigen Konzentration Arbeit verrichtet werden kann. Würde man c1und c2 vertauschen, so käme ΔG = +5,707 kJ/mol dabei heraus. Man hätte dann eine Bergaufdiffusion von der Seite der geringen Konzentration zur Seite mit der hohen Konzentration, und das würde natürlich Energie erfordern. Wenn man Wasser hochpumpen will, ist ja auch Energie erforderlich.
Wenn Ionen diffundieren, spielt natürlich die Ladung der Ionen eine Rolle, falls die Membran eine Spannung aufweist. Ist die Membranspannung U = 0, dann verschwindet der Term $z \cdot F \cdot U$. Das ist auch der Fall, wenn die Ladung z = 0 ist, wie es bei neutralen Molekülen vorkommt.
Schauen wir uns jetzt mal ein praktisches Beispiel an, wie es an der Membran einer Nervenzelle vorkommt. Die Membranspannung im Ruhezustand beträgt im Schnitt U = -70 mV. Die Konzentration der Natrium-Ionen auf der Außenseite der Zelle liegt bei Säugetieren bei 145 mmol/l, während die Innenkonzentration nur 12 mmol/l beträgt. Wenn sich die spannungsgesteuerten Natrium-Kanäle öffnen, strömen Natrium-Ionen mit hoher Geschwindigkeit von außen nach innen in die Nervenzelle. Bei einer Temperatur von 37 ºC oder 310 K berechnen wir dann Folgendes:
$\Delta G = 2,303 \cdot 0,008315 \frac{kJ}{mol \cdot K} \cdot 310 K \ \cdot log \frac{0,012}{0,145} + 1 \cdot 96,5 \frac{kJ}{V \cdot mol} \cdot -0,07 V$
$\Delta G = (5,936 \frac{kJ}{mol} \ \cdot -1,082) -6,755 \frac{kJ}{mol}$
$\Delta G = - 13,18 \frac{kJ}{mol}$
Das Membranpotenzial von -70mV hat also einen sehr großen Einfluss auf die Diffusion der Natrium-Ionen. Mit -6,755 kJ/mol trägt das elektrische Potenzial ungefähr genau so viel zur Diffusion bei wie das chemische Potenzial mit -6,422 kJ/mol. Beide Triebkräfte, elektrisches und chemisches Potenzial zeigen ja auch in die gleiche Richtung, nämlich ins Zellinnere. Die Zellinnenseite ist negativ geladen und zieht daher die positiven Natrium-Ionen an.