Populationswachstum

Für das Biologie-Abitur ist es wichtig, dass man zwischen exponentiellem und logistischem Populationswachstum unterscheiden kann.

Exponentielles Wachstum

Beim exponentiellen Wachstum gibt es quasi keine Grenze, die Population verdoppelt sich in einer bestimmten Zeiteinheit, beispielsweise jeweils in 10 Jahren.

Aus 100 Tieren werden dann in 10 Jahren 1.000 Tiere, in 20 Jahren 2.000 Tiere, in 30 Jahren 4.000 Tiere, in 40 Jahren 8.000 Tiere und so weiter.

Besonders extrem ist das exponentielle Wachstum bei Bakterien. Die Art Escherichia colie beispielsweise kann sich unter günstigen Bedingungen alle 20 Minuten teilen, also verdoppeln. Nach 6 Stunden haben sich aus einer Zelle bereits eine halbe Million Zellen gebildet, 20 Minuten später schon eine ganze Million.

Hyperexponentielles Wachstum

Wenn sich die Verdopplungszeit mit jeder Generation verkürzt, spricht man von einem hyperexponentiellem Wachstum. Die Menschheit ist lange Zeit hyperexponentiell gewachsen.

Logistisches Wachstum

In der Natur sind die Ressourcen wie Nahrung, Wasser und Platz begrenzt. Eine Population kann daher nicht unbegrenzt exponentiell wachsen. Irgendwann ist die Kapazitätsgrenze für die Population erreicht, und die Wachstumsrate wird wieder geringer, bis sie sich schließlich dem Wert 0 annähert. Man spricht dann von einer Stagnation oder umgangssprachlich von einem Nullwachstum.

Konkretes Beispiel

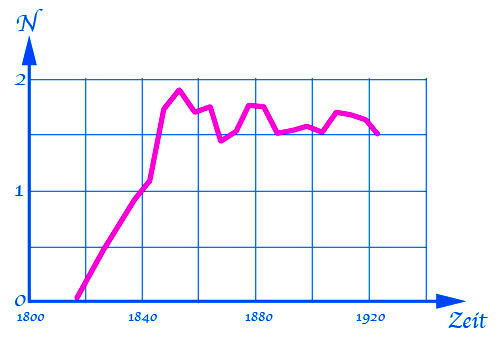
Wachstum einer Schafspopulation auf Tasmanien
Autor: Ulrich Helmich 2012, Lizenz: Public domain

Dieses Bild zeigt ein typisches logistisches Wachstum. In einer Anfangsphase, als die Schafe auf Tasmanien von Siedlern ausgesetzt wurden, konnten sie sich problemlos exponentielle vermehren, Gras gab es ja noch genug. Als sich die Tiere auf knapp 2 Millionen Exemplare vermehrt hatten, wurde die Nahrung aber knapp. Die Populationsgröße ging sogar auf 1,5 Mio. Tiere zurück, erholte sich dann aber wieder etwas, um danach um einen Mittelwert von 1,6 bis 1,7 Millionen zu schwanken.